Основы_акустики_Гринченко_Вовк

ная функция вида w(x,t) = w(x ± ct) уже не удовлетворяет уравнению. Физически это означает, что в стержне не может существовать волна произвольной формы, которая распространяется без изменения фор- мы с постоянной скоростью.

Однако это не означает, что в стержне вообще не могут распро- страняться волны. Легко проверить, что (6.280) допускает существо- вание гармонических волн

здесь μ — волновое число. Как видим, фазовая скорость изгибной волны в стержне

зависит от частоты, т.е. присутствует явление дисперсии. Соответст- вующая групповая скорость υгр = 2υф (убедитесь в этом самостоятель- но). Характер зависимости фазовой и групповой скоростей от часто- ты для изгибной волны в стержне совпадает с соответствующими за- висимостями (6.243), (6.244) для первой антисимметричной волны Лэмба в области малых волновых размеров толщины слоя (kth << 1). Это совпадение является естественным с учетом кинематики частиц среды в этих волнах.

Нужно помнить, что изложенная выше теория для изгибных волн в стержне хорошо описывает такой волновой процесс только для от- носительно низких частот, о чем шла речь при обсуждении характера напряжений и деформаций в стержне.

6.22. Волновое движение в стержне при заданных начальных условиях

Относительно простое уравнение движения (6.280) изгибных волн в стержне позволяет получить аналитическое решение задачи о волновом движении в стержне при определенных начальных условиях и тем самым изучить влияние дисперсии на форму возмущения, которое распространяется. Такое исследование можно провести, используя преобразование Фурье, смысл которого раскрывается двумя форму- лами [8]:

∞

ϕ(x) = ∫ Ф(k)exp(−ikx )dk,

−∞

401

Расширяя класс функций Ф(k), эти соотношения можно считать при- менимыми для любых физически содержательных функций ϕ(x).

Первое из равенств в (6.283), в сущности, указывает на возмож- ность представления любой функции в виде суперпозиции простран- ственных гармоник. Второе соотношение указывает на способ опре- деления плотности гармоник в такой суперпозиции по заданной функции ϕ(х). Соотношение (6.283) является обобщением на беско- нечный интервал разложения в ряд Фурье функций, заданных на ко- нечном интервале.

Рассмотрим теперь задачу об определении движения стержня в любой момент времени, если его начальное состояние задается равен- ствами

Если вместо искомой функции w(x,t) в рассмотрение ввести ее фурье- образ

то построение формального решения задачи значительно упростится. Перед тем как перейти непосредственно к нахождению функции Ф(k,t), приведем такое соотношение:

если функция w(x) стремится к нулю при x → ±∞. Последнее условие возьмем относительно не только искомой функции, но и ее первых производных, до четвертой включительно.

Соотношение (6.286) устанавливает такое правило: фурье-образ производной от заданной функции получаем простым умножением фурье-образа функции на величину ik. С использованием этого свой-

ства уравнение (6.280) для w(x,t) превращается в уравнение для

Ф(k,t). Для его определения умножим (6.280) на exp(ikx) и интегрируем по x :

402

с двумя произвольными функциями A(k) и B(k) от пространственного волнового числа k. Для их определения используем начальные условия (6.284), которые в терминах фурье-образов приобретают вид

Используя решение (6.288) для Ф(k,t), из последних равенств находим, что

Итак, решение поставленной задачи можно считать законченным. Искомая функция w(x,t) , которая удовлетворяет заданным началь-

ным условиям (6.284) и дифференциальному уравнению (6.280), представлена интегралом

Вычисление интеграла в явном виде по заданным функциям Q1(x) и Q2(x), как правило, осуществить не удается. Тем не менее, стандарт-

403

ные программы для вычисления быстрого преобразования Фурье при проведении численных расчетов на основе интегралов типа (6.291) входят в математическое обеспечение практически всех вычисли- тельных систем.

В конце параграфа рассмотрим случай начальных условий, кото- рый допускает явное вычисление интеграла в (6.291). Если начальные условия (6.284) таковы, что

(b — постоянная, м), то для функции смещения можно получить вы-

ражение [34, с. 178]:

(6.293)

Для случая струны при таком самом начальном возмущении имеем следующее выражение для смещения:

Понятно, что форма начального возмущения в стержне не будет сохраняться в процессе распространения. Этот вывод основывается на том, что общее возмущение является суперпозицией отдельных гармоник, а каждая гармоника распространяется со своей скоро- стью. Представление о влиянии дисперсии на развитие волнового про- цесса в стержне дает графическая интерпретация (6.293) и (6.294) в определенные моменты времени (рис. 6.38). На рис. 6.38 сплошной линией показано смещение в стержне (6.293), а штриховой — в струне (6.294) в отдельные моменты времени t; (в расчетах постоянные β, b и c равны единице).

Влияние дисперсии на рис. 6.38 показано очень наглядно. Состав- ляющим с довольно короткими длинами волн (большие k = 2π/λ) соот- ветствуют и высшие частоты в (6.291). Такие составляющие опере- жают низкочастотные составляющие и образуют некоторую рябь впереди основного гребня. Кроме того, длинноволновые составляю- щие согласно закону аномальной дисперсии распространяются очень медленно, что обусловливает появление слишком растянутого хвоста за основным гребнем. Следует также отметить, что основной гребень

404

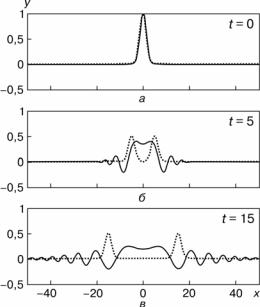
размывается дисперсией и его выделение со временем становится невозможным.

Рис. 6.38. Форма возмущения в бесконечных стержне (сплошная линия) и струне (штриховая линия) при начальных условиях (6.292) в разные момен- ты времени t

6.23. Изгибные колебания конечных стержней

В общем случае при рассмотрении движения конечного стержня естественно выделить задачи о свободных и о вынужден- ных колебаниях стержня. Здесь рассмотрим лишь задачу о свобод- ных колебаниях. После того как в рамках этой задачи будут проана- лизированы свойства нормальных колебаний конечного стержня, задача о вынужденных колебаниях под влиянием периодической си- лы уже не будет сложной. Рекомендуем решить такую задачу как упражнение.

Итак, условие рассматриваемой задачи следующее: стержень дли- ной l с закрепленными определенным образом концами начинает ко- лебаться в момент t = 0 при заданных начальных отклонениях и на- чальной скорости:

Определим дальнейшее движение стержня, которое характеризуется функцией w(x,t). Это означает, что необходимо найти решение урав- нения, которое удовлетворяет заданным граничным условиям и усло-

виям (6.295).

В связи с этим нужно подробнее остановиться на возможных слу- чаях граничных условий при изгибных колебаниях стержня. Важно понять, что эти условия должны формулироваться как ограничение на значение функции w(x,t) или ее производных в заданном сечении x = x0. При этом x0 будет иметь значение х0 = 0 или x0 = l.

Во многих практических ситуациях формулирование граничных условий, которые определяют характер взаимодействия данного эле- мента конструкции с другими элементами, является довольно слож- ной задачей. Рассмотрим лишь некоторые предельные случаи, кото- рые исключают отток энергии из стержня через его концы.

Первый из таких случаев — это случай свободного конца. Это оз- начает, что в сечении х = х0 на стержень не действуют никакие силы. Поскольку все силовые факторы в стержне характеризуются такими интегральными характеристиками, как изгибающий момент М и пе- ререзывающая сила Q, то в этом случае получаем такие условия: M(x0,t) = Q(x0,t) = 0. Для того чтобы выразить эти условия через функ- цию w(x,t), воспользуемся (6.274) и (6.278). При этом граничные усло- вия формулируются так:

Второй случай отвечает жесткому закреплению конца стержня. Ясно, что здесь на конце стержня не должно быть смещения w(x0,t). Однако этого условия не достаточно, чтобы полностью описать факт отсутствия движения на конце стержня. При нулевом смещении воз- можен поворот сечения. Такое движение будет невозможно, если по- требовать превращения в нуль на конце первой производной от w(x,t) по координате. Итак, условия жесткого закрепления торца стержня при изгибном деформировании, описываются равенствами

Предыдущие соображения указывают еще на одну возможность закрепления торца, когда исключается смещение w , но не наклады- ваются ограничение на поворот сечения. Это означает, что в таком сечении отсутствует внешний момент. Такие условия называются ус- ловиями шарнирного закрепления и описываются равенствами

406

Другие однородные комбинации с w и ее производными описывают условия, которые физически не реализуются.

Изучение свойств любой колебательной системы нужно начинать с нахождения ее нормальных колебаний. В данном случае это означает, что необходимо найти периодические решения уравнения, которые удовлетворяют одному из возможных типов граничных условий.

Подставляя в (6.280) выражение w(x,t) = X(x)exp(–iωt), находим та- кое уравнение для амплитудной функции X(x):

Общий подход к построению решения уравнений данного типа со- стоит в представлении искомой функции в виде X(x) = A exp(γx), где А — произвольная постоянная. Очевидно, что такое экспоненциаль- ное представление будет решением (6.299), если показатель γ опреде- лить из уравнения

Такому набору корней соответствует общее решение уравнения

(6.299):

Составляя разные линейные комбинации из частных решений, кото- рые входят в (6.302), искомую функцию можно представить в более удобном для дальнейших выкладок виде:

Полученное выражение удовлетворяет уравнению движения при лю- бых значениях частоты и постоянных а, b, с, d. Однако оно не удов- летворяет граничным условиям на концах стержня. Именно эти усло- вия определяют характерные частоты возможных периодических движений стержня.

Пусть один конец стержня (x = 0) жестко закреплен, а другой (x = l)

— свободен. Такие условия могут довольно хорошо описывать ситуа- цию на концах ножки камертона. Согласно (6.296) и (6.297) для функции X(x) в (6.303) будем иметь условия

407

Граничные условия при x = 0 дают следующую связь между искомы- ми величинами: d = –a, c = –b. Удовлетворение условий второй пары (6.304) приводит к системе линейных однородных уравнений второго порядка:

a [ch(μl) + cos(μl)]+b [sh(μl) + sin(μl)] = 0,

Условие наличия ненулевого решения для постоянных a и b преду- сматривает равенство нулю определителя системы (6.305), что приво- дит к уравнению

Рис. 6.39. Графическое решение уравнения (6.306)

Именно отсюда будем определять допустимые значения величины μ, а, следовательно, и частоты нормальных колебаний. Это трансцен- дентное уравнение, которое имеет бесконечное число корней. Харак- терные особенности (6.306) и даже достаточно точные оценки значе- ний его корней с высокими номерами можно получить из его графи- ческой интерпретации (рис. 6.39).

Для трех первых корней имеем такие значения: μ1l = 1,8751; μ2l = 4,6941; μ3l = 7,8548. На рис. 6.31 видно, что корни с высокими номерами определяются по приближенной формуле:

408

Уже для случая n = 3 эта формула дает три правильных знака в зна- чении корня. Если учесть, что μl = β ωl (определение β см. (6.282)), то для низких собственных частот имеем:

Как видим, частоты нормальных колебаний в стержне обратно пропорциональны квадрату его длины. У струны собственные часто- ты обратно пропорциональны длине. В случае равенства основного тона стержня и струны вторая собственная частота стержня уже вы- ше частоты шестой гармоники. Важно также отметить, что собствен- ные частоты стержня не образуют гармонический ряд. Следствием этого является, например, особенность звучания камертона. При уда- ре по концу ножки в нем возмущается много нормальных колебаний. Поскольку их частоты не создают гармонический ряд, то в начальный момент слышен только металлический звон. Потом высокочастотные собственные колебания быстро затухают, и далее остается слышимым чистый основной тон.

Если при μ = μn одно из уравнений системы (6.305) использовать для установления связи между постоянными an и bn, то на основе (6.303) получим выражение для собственной формы колебаний стержня:

Очевидно, что все сформулированные условия, которые опреде- ляют нормальные колебания, остаются выполненными, если получен- ное выражение Xn(μn,x) умножить на произвольную постоянную bn. Значение этой постоянной определяет степень возмущения соответ- ствующей собственной формы и находится из начальных условий.

На рис. 6.40 показано распределение амплитуд колебаний по дли- не стержня для пяти первых собственных форм Xn (μn ,x). Видно, что

с ростом номера формы вклад экспоненциальных слагаемых (ch(μnx), sh(μnx)) все больше локализуется на концах стержня.

Полное выражение для функции смещения получим из выражения (6.309) после умножения его на временной множитель. В общем случае фаза нормального колебания может быть произвольной, итак,

wn (x,t) = bn cos(ωnt + ϕn ) {[sh(μn x) − sin(μn x)][sh(μnl) − sin(μnl)] − sh(μnl) − sin(μnl)

409

Произвольные постоянные bn и ϕn определяются из начальных усло- вий.

Рис. 6.40. Распределение амплитуд колебаний для первых пяти собственных форм стержня

Дальнейшее решение задачи определения движения стержня по заданным начальным условиям основывается на фундаментальном предположении: какими бы ни были начальные условия в (6.295), дальнейшие колебания стержня полностью описывается суперпози- цией нормальных колебаний с соответствующим образом подобран- ными амплитудами. Итак, колебания стержня описывается выраже- нием для w(x,t) в виде бесконечного ряда

∞

w(x,t) = ∑ wn (x,t). (6.311) n =1

Бесконечный ряд (6.311) имеет две последовательности произвольных постоянных — bn и ϕn. Для их определения имеем два условия:

С использованием обозначений (6.309) и (6.310) эти соотношения приобретают вид

∞

∑ bn cos(ϕn )Xn (μn ,x) = Q1(x), n =1

410