Основы_акустики_Гринченко_Вовк

Также самостоятельно убедитесь в том, что при определении сред- него потока мощности вдоль поверхности полупространства (вдоль оси Ox1) принцип суперпозиции не работает. Для данной задачи наблю-

дается направленный поток мощности вдоль свободной границы, причем плотность потока зависит от величины пространственной координаты x3 .

Используя выражение для плотности среднего потока мощностиP3 = − ω2 Re (iσ31u1 + iσ33u3 ) и данные параграфа 6.9 можно получить

(сделайте самостоятельно) формулы для относительных величин энер- гий, которые уносят отраженные Р- и SV-волны при падении

Рассмотрим численные результаты. На рис 6.16 показанные от- носительные величины энергий, которые уносят отраженные Р- и SV-волны (рис. 6.16, а, б - при падении Р-волны, рис. 6.16, в, г - при падении SV-волны), как функции угла падения θ для разных значе- ний коэффициента Пуассона ν . Как видим, распределение энергии между отраженными волнами имеет сильную зависимость как от уг- ла падения, так и от коэффициента Пуассона. В целом сравнение графиков на рис. 6.16 говорит об отсутствии качественных отличий в процессах отражения продольных и поперечных волн при докри- тических углах падения.

Приведенные кривые интересные также с точки зрения энерге- тического анализа отражения в условиях полного преобразования волн. Как для Р-волны, так и для SV-волны при ν < ν = 0,2637 имеем

два значения угла падения, при которых наблюдается полное преоб- разование падающей Р-волны в SV-волну (рис. 6.14) и полное преоб- разование падающей SV-волны в Р-волну (рис. 6.15, а). Для случаев относительно близких значений этих углов (величина ν близка к ν ), как видно из кривых 2 (ν = 0,25) на рис. 6.16, существует довольно

широкий диапазон углов падения θ, для которых энергия, которую приносит падающая волна одного типа, практически полностью уносится волной другого типа. Для малых значений ν наблюдается

351

сужение указанного диапазона углов, для которых полное превра- щение волн энергетически четко выражено (кривые 1 на рис.6.16). При этом для большего по величине угла падения диапазон углов, в котором наблюдается явление преобразования типа волны, чрезвы- чайно узкий.

Рис. 6.16. Зависимость коэффициентов Eee (а), Eet (б), Ett (в), Ete (г) от

угла падения θ при разных значениях коэффициента Пуассона: кривые 1— 4 при значениях ν соответственно 0,15; 0,25; 0,35; 0,4

6.11. Поверхностная волна Рэлея

Вспомним колебательную систему с двумя степенями сво- боды. При исследовании системы с двумя степенями свободы (см. па- раграфы 2.5 и 2.6), были записаны два дифференциальных уравне- ния движения. Если считать, что внешняя сила не действует на коле- бательную систему, то получаем систему дифференциальных уравне- ний с нулевой правой частью. Такие уравнения описывают свобод-

352

ные колебания в системе с двумя степенями свободы. Далее, учиты- вая гармоническую зависимость от времени свободных колебатель- ных движений, получаем систему линейных алгебраических уравне- ний относительно амплитуд колебаний в каждой парциальной систе- ме. Однородная система алгебраических уравнений имеет решение, если ее определитель равен нулю. Анализ уравнения (равенство нулю определителя) показывает, что искомых свободных колебаний в сис- теме может быть два. Такие колебания получили название собствен- ных, или нормальных, колебаний. Они характеризуются собственной частотой и собственной формой, т.е. отношением амплитуд колеба- ний в парциальных системах. Можно сказать, что нормальные коле- бания — это свободные колебания в системе при специфических на- чальных условиях, когда система, при отсутствии потерь, сохраняет форму колебаний бесконечно долго. В режиме вынужденных колеба- ний явление резонанса в колебательной системе наблюдается, когда частота внешней силы равна одной из собственных частот системы. При этом в системе без демпфирования амплитуда колебаний в обеих парциальных системах стремится в бесконечность. Такие характер- ные свойства, как мы не раз убеждались, наблюдаются и при исследо- вании других колебательных систем.

Вернемся к рассмотренной выше задаче о падении плоской волны на свободную границу полупространства, и под другим углом зрения посмотрим на полученные решения (6.138), (6.139) и (6.152), (6.153).

Они являются решениями соответствующих алгебраических систем уравнений (6.136), (6.137) и (6.150), (6.151). Если определитель этих систем (а он одинаков для обеих систем (6.136), (6.137) и (6.150), (6.151)) приравнять к нулю, то будем иметь выражение, которое стоит в знаменателе решений (6.138), (6.139) и (6.152), (6.153). Итак, при условии равенства нулю определителя, а отсюда и знаменателя реше- ний, будем иметь бесконечные значения коэффициентов отражения, т.е. бесконечный рост амплитуд отраженных волн. Проводя паралле- ли с исследованием колебательной системы с двумя степенями свобо- ды, можно считать, что нахождение корней уравнения в виде равно- го нулю определителя означает исследование собственных волновых движений полупространства со свободной границей.

Проведем такое исследование. Приравнивая нулю знаменатель в указанных выше решениях, записываем такое уравнение:

Несколько преобразуем это уравнение. Принимая во внимание, что

радикалов. Тогда получим

353

Выражение (6.166) можно рассматривать как уравнение относитель- но компоненты волнового вектора вдоль границы. Поскольку k = ω/c,

Это уравнение относительно величины c/ct имеет единственный дей- ствительный корень, который лежит между 0 и 1. Действительно, под- ставляя вместо c/ct нуль, получаем отрицательное число; подставляя вместо c/ct единицу, получаем положительное число. Т.е., между ну- лем и единицей должен быть искомый корень. (Можно провести стро- гое доказательство существования и единственности корня на ука- занном интервале.) В качестве примера на рис. 6.17 приведен гра- фик функции R(c/ct) на отрезке [0,1] при значении коэффициента

Пуассона ν = 0,3 (здесь ct2 /ñe2 ≈ 0,286 ). Видно, что существует един- ственный корень c = cR.

Рис. 6.17. График функции R(с/сt) при ν = 0,3

Каков физический смысл полученного решения? Поскольку cR < ct, а, значит, и cR < ce, то исследуемая бегущая волна вдоль границы распространяется медленнее, чем поперечная и продольная волны. Иначе, величина kR = ω/cR больше волновых чисел Р- и SV-волн (kR > kt, kR > ke). Таким образом, Р- и SV-волны в этом случае являются неоднородными.

Итак, звуковое поле в полупространстве можно представить как совокупность двух неоднородных волн: одна — продольного типа и вторая — поперечного. Эти волны распространяются вдоль границы с фазовой скоростью cR и затухают в направлении от границы в глуби- ну полупространства (вдоль оси Ox3).

354

Запишем выражения для векторов смещений в неоднородных Р- и SV-волнах. Обозначим

ηe = ke2 −kR2 = i kR2 −ke2 = iηe(R ), ηt = kt2 −kR2 = i kR2 −kt2 = iηt(R ) (6.168) (поскольку kR > kt, kR > ke). Из однородной системы (6.150), (6.151) (в правой части уравнений имеем нули, поскольку падающей волны нет) получим связь между амплитудами волн. Так, из уравнения (6.150) имеем

Выражение для неоднородных волн получим из формул (6.148), (6.149) для однородных SV- и Р-волн с учетом новых обозначений и формулы (6.169):

здесь V — постоянная; напомним, что в полупространстве координа- ты x3 отрицательные, поэтому при распространении волн в глубину

полупространства амплитуды уменьшаются.

Подставив суперпозицию волн (6.170) и (6.171) u = ue + ut в гра- ничные условия (6.134), (6.135), можно убедиться, что они выполня- ются (рекомендуем провести эти преобразования). Итак, суперпози- ция неоднородных волн продольного и поперечного типов действи- тельно делает свободной от напряжения границу полупространства.

Следует отметить, что уравнение (6.167) имеет другие действи- тельные и комплексные корни, которые определяют разные комби- нации продольных и поперечных волн, обусловливающие нулевое зна- чение напряжения на границе. Но решение в виде поверхностной волны одно и соответствует действительному корню cR < ct.

Итак, полученное поле можно интерпретировать как самостоя- тельную поверхностную волну сложной структуры, которая может существовать в твердом теле (подобно тому, как мы определяли нор- мальные колебания в системе с двумя степенями свободы). Впервые существование поверхностных волн в твердом теле предсказал Рэлей

355

в 1885 г. Поэтому эту поверхностную волну называют рэлееськой волной (или волной Рэлея), а уравнение (6.160) — уравнением Рэлея.

Рис. 6.18. Зависимость относительной скорости рэлеевськой волны от ко- эффициента Пуассона среды

Таким образом, рэлеевська волна распространяется вдоль грани- цы с фазовой скоростью cR = ω/kR, которая меньше скорости попе- речной волны ct. Важно отметить, что коэффициенты уравнения (6.167) не зависят от частоты, а, следовательно, и фазовая скорость cR волны Рэлея не зависит от частоты, т.е. волна Релея распространяется без дисперсии (произвольный импульс возбуждения сохраняет свою форму при распространении). Значение cR зависит от коэффициента Пуассона среды ν и монотонно изменяется от 0,87ct при ν = 0 до

0,96ct при ν = 0,5 (рис. 6.18).

Можно получить приближенную формулу для вычисления скоро- сти волны Рэлея. Для этого, поделив исходное дисперсионное уравне- ние (6.165) на k4 и учитывая то, что справедливы неравенства kR > kt,

где s = kt/k = c/ct, q2 = ce2 /ct2. Возьмем в качестве начального при-

ближения c = ct. Тогда искомое значение с представим в виде выра- жения, которое учитывает только линейные по отклонению с от ct сла- гаемые, именно: c = ct(1 – δ), откуда s = 1 – δ.

Подставим s = 1 – δ в уравнение (6.172), потом возведем его в квадрат и, учитывая только линейные члены по δ, придем к уравне-

нию 8δ(4 − 3q2 )+ q2 = 0 . С учетом формулы (6.140), определяем вели-

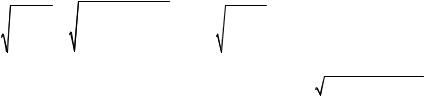
Из соотношений (6.176) и (6.177) видно, что частицы в волне Рэлея перемещаются по эллиптическим орбитам. Для величины ν = 0,25 от- ношение меньшей полуоси эллипса (u1) к большей (u3) при x3 = 0 при- близительно равняется 0,694. Изменение коэффициента Пуассона ν от 0 до 0,5 приводит к изменению этого отношения от 0,556 до 0,788.

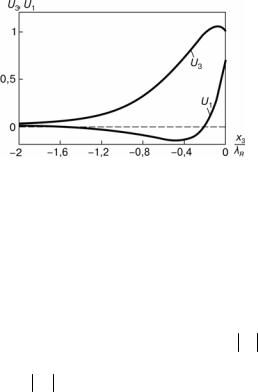
Рис. 6.19. Нормированные зависимости амплитуд U1 и U3 компонент вектора смещения частиц в волне Рэлея от расстояния до границы x3/λR; ν = 0,25

На рис. 6.19 показаны величины амплитуды вертикальных U3 и горизонтальных U1 смещений, нормированные к амплитуде компо- ненты u3 на поверхности границы (x3 = 0), ν = 0,25. Как видим, вер- тикальное смещение (u3) достигает максимума на расстоянии 0,08λR от поверхности, а потом плавно падает, не изменяя знак. Горизон- тальное смещение (u1) становится равным нулю при x3 = –0,19λR, а по- том изменяет направление. Таким образом, при x3 < 0,19λR движе-

ние частиц среды происходит по эллиптическим орбитам против ча- совой стрелки, а при x3 > 0,19λR — по часовой стрелке (объясните

почему).

Энергетический анализ волны Рэлея показывает, что средняя за период нормальная к границе составляющая потока мощности тож- дественно равна нулю. Средняя за период величина потока мощности вдоль границы отлична от нуля и положительна. Оказывается, что практически вся энергия, которая переносится волной Рэлея, сосре- доточена в слое толщиной λR.

Волны Рэлея играют важную роль в сейсмических явлениях: по- скольку они являются поверхностными, то они расходятся при рас- пространении от источника волн только в двух измерениях (напри- мер, при землетрясении - вдоль земной коры) и потому затухают мед- леннее, чем обычные продольные и поперечные волны, которые рас- пространяются в объеме среды. Поэтому поверхностные волны можно наблюдать на таких больших расстояниях от эпицентра землетрясения, на которых волны других типов уже не заметны. Волны Рэлея мегагер-

358

цового диапазона широко используются в дефектоскопии для регист- рации поверхностных трещин и в акустоэлектронных устройствах для обработки сигналов.

6.12. Волны в твердом полупространстве, возбуждаемые пространственной гармоникой

В ультразвуковом неразрушающем контроле изделий из ме- талла и других упругих материалов почти всегда наблюдается такая ситуация: предполагаемый дефект расположен в толще детали, а дос- туп возможен только к ее поверхности. Тогда возникают важные, с практической точки зрения, вопросы: какое возбуждение нужно соз- дать на поверхности, чтобы в толще детали распространялись нужные для неразрушающего контроля волны или какие волны будут распро- страняться в объеме детали при заданном возбуждении поверхности?

Попробуем исследовать эти вопросы на модели твердого полупро- странства с плоской границей, хотя найдется немного изделий, похо- жих на полупространство. Обычно имеется несколько граничных по- верхностей, причем необязательно плоских. Однако нередко влиянием всех границ, кроме той, где приложено возбуждение, можно пренебре- гать. Это бывает в случаях, когда несущественна интерференция пря- мой и отраженной волн – то ли вследствие импульсного характера воз- буждения, то ли вследствие малой амплитуды отраженного сигнала. Что касается локального искривления поверхности, то им можно в первом приближении пренебрегать, если радиус кривизны достаточно большой в сравнении с длиной волны. Таким образом, закономерно- сти, присущие твердому полупространству, могут быть разумно пере- несены на практически интересные случаи.

Пусть на поверхности твердого полупространства располагается источник, который создает возбуждение на некоторой части этой по- верхности. Другая часть поверхности полупространства по обыкнове- нию граничит с другой упругой средой. Если этой средой является воздух (а это типичная ситуация), можно, вследствие резкого отличия плотности и упругих свойств таких материалов как металлы и воздух, пренебрегать реакцией воздушной среды и рассматривать эту часть границы как свободную, т.е. как границу с вакуумом.

Источник представляет собой некоторый объем активного материа- ла (например, пьезопластина), к которому подводится электрическое напряжение. Строго говоря, необходимо рассматривать взаимодейст- вие этого материала с упругой средой и поставить, так называемую, контактную задачу электроупругости. Решение такой задачи, как пра- вило, довольно сложное. Но в некоторых случаях вместо постановки контактной задачи удается задать на участке, где действует источник,

359

параметры движения поверхности твердой среды (т.е. поставить более простую граничную задачу).

Это возможно в тех случаях, когда параметры источника и среды резко отличаются. Например, когда материал источника имеет значи- тельную плотность и практически несжимаемый. Тогда смещение по- верхности среды будет определяться смещением поверхности источ- ника. Следовательно, можно задавать смещение частичек среды на участке поверхности, которая занятая источником. При противопо- ложном соотношении свойств материала источника и среды на том же участке можно задавать компоненты тензора напряжения (например, когда между источником и металлом присутствует слой жидкости). Нужно подчеркнуть, что ряд практически важных закономерностей проявляются одинаково в граничных и контактных задачах. Поэтому методически будет правильно, если мы рассмотрим их на примере граничной задачи.

Пусть на поверхности x3 = 0 твердого полупространства x3 ≤ 0 оп- ределены компоненты тензора напряжений (рис. 6.20) σ31 (x1,x2,t ) , σ32 (x1,x2,t ), σ33 (x1,x2,t ). Рассматриваем плоскую задачу, при кото- рой параметры возмущения не зависят от координаты x2 . Необходимо определить упругие волны, которые возникают в среде.

Рис. 6.20. Упругое полупространство ( x3 ≤ 0 )

Будем считать, что напряжение σ31 , σ32 и σ33 изменяются во времени по гармоничному закону (в дальнейшем временной множи- тель exp(−iωt ) не пишем). Такое рассмотрение является целесообраз-

ным, ведь, используя метод Фурье, можно получить решение и для не гармонического во времени возбуждения источника.

Метод Фурье, в основе которого лежит представление о том, что практически любую сложную функцию одной или нескольких пере-

менных, например σ(x1,x3 ), можно представить в виде суммы гармо-

нять и при исследовании поля источника произвольной формы.

360