Основы_акустики_Гринченко_Вовк

дела двух твердых сред. Однако исследование такой задачи в общем случае, как это было сделано для жидких сред в параграфе 5.5, доста- точно громоздкое. Поэтому мы остановимся на важном частном случае падения плоской гармонической волны на свободную плоскую границу полупространства.

Падающую волну на границу будем считать или продольной волной (Р-волна), или поперечной волной с поляризацией в плоскости падения волны (SV-волна), или поперечной волной с поляризацией, перпендику- лярной к плоскости падения (SH-волна). Любую поперечную волну мож- но представить как суперпозицию волн этих двух линейных поляриза- ций.

Усложнение поставленной задачи для твердого тела по сравнению с жидкостью состоит в том, что при падении одной волны на границу образуются сразу две отраженные волны — и продольная, и попереч- ная. Увеличение количества отраженных волн по сравнению с жид- костью обусловлено увеличением числа условий на границе твердой среды.

Исключением является падение SH-волны (в этой волне поляриза- ция перпендикулярна к плоскости падения волны). Если х1Ох3 — плоскость падения волны, х1Ох2 — плоскость границы, то поляриза- ция SH-волны будет происходить вдоль оси Ох2. Поскольку частицы среды смещаются вдоль оси Ох2, то на свободной границе (плос- кость х1Ох2) можно рассматривать только одно условие — для каса- тельного напряжения σ32 = 0. Поэтому, отражаться от границы, как и в случае жидкого полупространства, будет одна волна с той же поля- ризацией (SH-волна). Коэффициент отражения по смещению SH- волны от свободной границы равен единице с плюсом, а для жесткой, т.е. границы вдоль которой нет скольжения, единице с минусом. Ре- шение общей задачи о падении SH-волны на границу раздела двух твердых сред можно исследовать самостоятельно.

Рассмотрим теперь более интересный случай падения Р-волны или SV-волны на свободную границу твердого тела. Для такой ситуации, характерной особенностью процесса отражении от свободной грани- цы является наличие в общем случае отраженных Р- и SV-волн. В бес- конечном пространстве Р- и SV-волны могут распространяться неза- висимо. Наличие же свободной границы обусловливает связь двух типов волновых движений.

Анализ задачи об отражении и прохождении звука на границе жидких сред (параграф 5.5) позволяет, используя закон Снелиуса, ут- верждать, что касательные к границе полупространства компоненты

шими стрелками показаны волновые векторы — ke для Р-волны, kt

341

для SV-волны; маленькие стрелочки иллюстрируют условно выбран- ное положительное направление колебаний частиц среды в соответ- ствующей волне (для Р-волны вдоль направления движения волны, а для SV-волны перпендикулярно к направлению движения волны и против часовой стрелки).

Рис. 6.13. Лучевая картина взаимодействия Р-волны (а) и SV-волны (б) со свободной границей твердого тела (плоскость х1Ох2)

В случае падения Р-волны на границу (рис. 6.13, а) имеем

В случае падения SV-волны на границу (рис. 6.13, б) получаем

342

Итак, мы получили формулы, которые позволяют вычислить ко- эффициенты отражения Vee и Vet, если заданы угол падения θ про- дольной волны и коэффициент Пуассона ν среды. Для нормального падения (θ = 0°) имеем Vee = –1, Vet = 0, т.е. полное отражение Р-волны без образования SV-волны. Значение Vee = –1 при θ = 0° определяет удвоенную амплитуду колебаний частиц среды на поверхности сво- бодной границы (убедитесь в этом, расписав, согласно формул

(6.128)—(6.130), сумму ue + uee + uet при θ = 0° и x3 = 0).

В случае θ = 90° (скользящее падение) имеем Vee = –1 и Vet = 0. Если теперь вычислить вектор смещения частиц среды на поверхности

свободной границы, то получим ue + uee + uet = 0 (θ = 90°), т.е. движе- ние отсутствует. Это обстоятельство является указанием на то, что

соотношение (6.126) не справедливо в случае скользящего падения Р- волны. При оценке указанного парадокса нужно иметь в виду, что рас- сматривается задача об отражении плоской гармонической волны, и вопрос об источнике плоской волны не обсуждается. Поэтому такая по- становка задачи приводит к указанному противоречию при скользя- щем падении Р-волны, но для всех других углов падения дает нагляд- ную картину взаимодействия упругих волн с плоской границей.

Рис. 6.14. Зависимость коэффициента Vee от угла падения θ при разных значениях коэффициента Пуассона: кривые 1—4 при значениях ν соответ-

ственно 0,15; 0,25; 0,3; 0,4

На рис. 6.14 показана зависимость коэффициента Vee от угла па- дения при разных значениях коэффициента Пуассона. Из рисунка следует, что при некоторых значениях ν и углах падения θ амплитуда отраженной Р-волны равна нулю, т.е. падающая Р-волна в процессе отражения полностью превращается в поперечную SV-волну. Соот- ветствующий энергетический анализ процесса отражения Р-волны позволяет убедиться, что в таких ситуациях энергетический коэффи- циент отражения для SV-волны равен единице (см. ниже параграф

345

6.10). Из выражения (6.139) для Vee видно, что это происходит при выполнении равенства

Анализ этого соотношения показывает, что существует критическое зна- чение ν = 0,2637 . Если в среде ν < ν , то уравнение (6.143) имеет два

действительных корня для угла падения в диапазоне (0°, 90°). При ν > ν таких корней нет, т.е. при любых углах падения амплитуда от- раженной Р-волны не равна нулю.

Рассмотренный случай отражения Р-волны от границы полупро- странства характеризуется также тем, что изменение угла падения не приводит к качественному изменению в волновой картине, т.е. мы всегда имеем отражение в виде распространяющихся волн. Другими словами, приведенная на рис. 6.13, а лучевая картина процесса от- ражения продольной волны описывает характерные черты физики явления, за исключением случая скользящего падения (θ = 90°).

Теперь рассмотрим падение на свободную границу полупростран- ства гармонической с частотой ω SV-волны единичной амплитуды. Как увидим в дальнейшем, здесь ситуация может существенно изме- нится. Запишем выражения для векторов смещения в падающей SV-

Перепишем выражения (6.144)—(6.146), используя соотношения kt sinθ = k, kt cosθ = ηt, ke cosθe = ηe, sinθe = (kt/ke)sinθ = k/ke:

Расписывая граничные условия (6.134) и (6.135), получаем систему линейных алгебраических уравнений относительно коэффициентов

Vee и Vet :

346

При θ > θкр процесс отражения поперечной волны уже невозможно объяснить с точки зрения лучевого представления. Это обусловлено тем, что при θ> θкр продольная волна становится неоднородной вол-

ной, свойства которой мы детально изучили в п. 5.5.4. Количественный анализ процесса отражения можно провести со-

гласно формул (6.154), (6.155) и при θ > θкр. В ситуации, когда θ > θкр имеем q sin θ > 1, тогда 1 − q2 sin2 θ является мнимой величиной:

где q определяется формулой (6.140). При закритических углах паде- ния (θ > θкр) физическое решение получается после умножения выра- жений (6.147)—(6.149) на exp(–iωt) и выделения действительной части в компонентах векторов смещений.

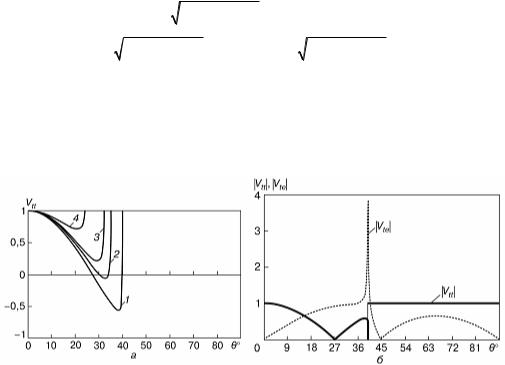
Рис. 6.15. Зависимость коэффициентов отражения Vtt(а — ν = 0,15; 0,25;

0,30; 0,40 — кривые 1—4) и Vtt , Vte (б — ν = 0,15; θкр ≈ 39,92°) от угла па-

дения θ

На рис. 6.15, а приведены зависимости изменения коэффициента отражения SV-волны Vtt от угла падения θ для разных значений ко-

эффициента Пуассона. Вычисления выполнены для углов, меньше критического, поэтому рис. 6.15, а характеризует также зависимость критического угла θкр от коэффициента Пуассона ν. При θ > θкр со- гласно выражениям (6.154) и (6.157) имеем Vtt = 1, поскольку, как мы уже знаем, средний поток мощности вдоль оси Ох3 в неоднород- ной продольной волне равен нулю.

Как и на рис. 6.14, здесь также наблюдается полная трансформа- ция энергии падающей на границу SV-волны в продольную волну (этому эффекту соответствуют точки пересечения кривых и оси абс-

348

цисс). Это происходит при значениях коэффициента Пуассона ν, мень- ших некоторого ν . Величина ν определяется при анализе того же уравнения (6.143), что и в случае падения Р-волны, и равна 0,2637. Но углы падения, при которых происходит полное преобразование поперечной волны в продольную волну, будут, безусловно, другими.

На рис. 6.15, б показана зависимость модулей коэффициентов от- ражения Vtt и Vte от угла падения θ при ν = 0,15 (ce /ct =1,56 ).

Интересной особенностью отражения продольной волны является резкий рост величины Vte в окрестности критического угла падения θкр = 39,92°. Такой рост коэффициента Vte не должен беспокоить, ведь поток энергии определяется кинематическими и силовыми фактора- ми волнового поля (см. далее параграф 6.10). В отдельных случаях (θ ≈ 27,3°; 39,88° на рис. 6.15, б) энергия, которую уносит отраженная SV- волна, равна нулю, а отраженная Р-волна переносит всю энергию па- дающей SV-волны.

Кроме случая полного преобразования одного типа движения в другой в процессе отражения от свободной границы не меньший ин- терес представляет случай полного сохранения типа движения (си- туация нормального падения волны является очевидной). Если падает Р-волна, то согласно (6.142) условием сохранения типа движения бу-

дет уравнение q2 − 2sin2 θ = 0 . Но выполнение этого условия невоз- можно, поскольку имеем sinθ = q 2 = (1−v)/(1− 2v) >1 (см. (6.140)), что невозможно. При падении SV-волны в соответствии (6.155) имеем

условие: 1 − 2sin2 θ = 0 . Отсюда θ = 45°. На рис. 6.15 такое значение угла падения закритическое, и, следовательно, при отражении SV- волны возбуждается неоднородная продольная волна. В качестве

примера (рис. 6.15, б) при θ = 45° имеем Vtt = 1 и Vte = 0, т.е. про- дольная волна не возбуждается.

Подводя итоги проведенного анализа задачи отражения волны от свободной границы твердого полупространства, следует отметить, что полученные результаты представляют интерес при исследовании вол- новых и колебательных процессов в твердых телах конечных разме- ров.

6.10. Энергетический анализ процесса отражения плоской гармоничной волны от свободной границы полупространства

Рассмотрим энергетические характеристики процесса от- ражения Р-волны (рис. 6.13, а) и SV-волны (рис. 6.13, б ) от свободной границы полупространства. Предметом анализа являются энергетиче-

349

ские коэффициенты отражения, которые характеризуют распределе- ние потока энергии падающей волны между отраженными волнами.

Плотность потока мощности P в твердом теле определяется соот- ношением

где σ - тензор напряжения, u - вектор смещения. В декартовых коор- динатах, для нашей плоской задачи (рис. 6.13), определение потока мощности будет иметь вид

При записи этих соотношений координаты тензора напряжения и век- тора смещения являются действительными функциями.

При анализе гармоничных волновых процессов (exp(−iωt))обычно рассматривают не мгновенное, а среднее за период T = 2π/ω значение

потока мощности (см. формулу (4.51)). Тогда используя комплексную форму записи, согласно (4.55), среднее значение плотности потока мощности P определяется так:

Компоненты вектора P в декартовых координатах будут иметь вид

В записанных формулах компоненты вектора P выражаются через

комплексные амплитуды компонент тензора напряжения и вектора смещения.

Предлагаем читателю убедится самостоятельно в том, что для обоих случаев падения Р- и SV-волн оказывается справедливым принцип су- перпозиции средних потоков мощности P3 , которые переносятся

отдельными волнами. Таким образом, в направлении нормали к сво- бодной границе (вдоль оси Ox3 ) имеют место такие энергетические

соотношения:

Именно этот факт делает физически обоснованным раздельное вы- числение средних потоков мощности в каждой волне с целью на- глядного изображения энергетических соотношений.

350