Основы_акустики_Гринченко_Вовк

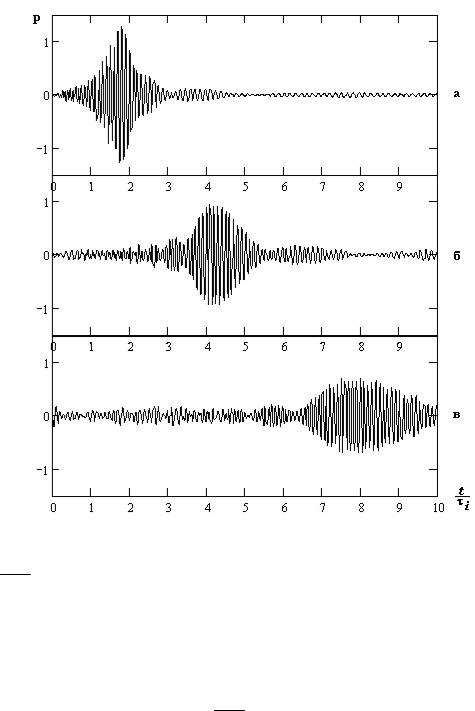
Рис. 5.34. Временные зависимости давления при распространении сигнала

1, ωкр1 = 60 , z /h = 0,5 :

Ωi

а - x′ = 50 , б - x′ =150 , в - x′ = 300

Сосредоточим наше внимание на распространении сигнала 1. На рис. 5.32, 5.33 и 5.34 показаны временные зависимости давления в точках наблюдения с координатами x′ = 50,150,300 , z /h = 0,5 при

разных значениях параметра ωкр1 = 20,40,60 . Вдоль оси абсцисс от-

Ωi

ложено нормированное время t′ = tτi . При этом отброшено время

281

распространения импульса со скоростью c , т.е. величина

t′ = x 1 = x′ . Анализируя графики на рис. 5.32-5.34, можно отметить c τi N

две характерные особенности в изменении структуры исходного сиг- нала 1, которые накапливаются при его распространении. Первая особенность – это задержка сигнала в сравнении со временем рас-

пространения t , вторая – растягивание во времени продолжительно- сти сигнала в сравнении с начальной длительностью импульса τi .

Рис. 5.35. Значения фазовой υф(1) /с (кривые 1,2,3) и групповой υ(1)гр /с

(кривые 1,2′ ′,3′) скоростей первой моды составляющих сигнала (5.225) при разной величине параметра ωкр1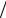Ωi :

1,1′ - ωкр1Ωi = 20 , 2,2′ - 40 , 3,3′ - 60

Как видно, отмеченные эффекты существенно зависят от величи- ны критической частоты первой моды ωкр1Ωi . Для объяснения этой

зависимости обратимся к графикам на рис. 5.35, которые определя- ют фазовую υф(1) и групповую υ(1)гр скорости первой моды составляю- щих сигнала (5.225) при разных величинах параметра ωкр1Ωi . На- помним, что в полосе частот [ω90,ω110 ] сосредоточенно 90% всей

энергии сигнала 1 (рис. 5.29, а). Как видим, чем меньше величина параметра ωкр1Ωi , тем в меньшей степени изменяются значения

282

скоростей υф(1) и υ(1)гр в окрестности частоты несущей ω0 = ω100 , и,

следовательно, тем дольше будет сохраняться исходная форма сигна- ла 1 при его распространении.

Проведем количественную оценку эффекта задержки во времени сигнала 1 при его распространении в сравнении со временем t . Здесь возможны различные подходы, поскольку возникает необходи- мость фиксировать момент прихода импульсного сигнала, который претерпевает изменение своей формы в процессе распространения. Проведем эту процедуру, опираясь на понятие групповой скорости. Поскольку сигнал 1 (см. рис. 5.29, а) можно считать узкополосным, то его групповую скорость определим как групповую скорость первой моды на частоте несущей ω0 , т.е.

Рис. 5.36. Зависимость групповой скорости υгр /c распространения сигна- ла 1 от параметра ωкр1Ωi при величине Nq =100

Зависимость групповой скорости υгр от параметра ωкр1Ωi пока- зана на рис. 5.36, она позволяет оценить уменьшение υгр при увели- чении величины ωкр1Ωi . Тогда временную задержку t прихода им-

пульсного возмущения в точку наблюдения с координатой x′, в срав- нении со временем распространения t , можно определить так:

где

283

Рис. 5.37. Зависимость временной задержки t′ от расстояния пробега x′ сигнала 1 для разных значений параметра ωкр1Ωi ; Nq =100 :

1 - ωкр1Ωi = 20 , 2 - 40 , 3 - 60

На рис. 5.37 показана зависимость временной задержки t′ от нормированного расстояния x′ = xλ0 пробега сигнала 1 для разных

значений параметра ωкр1Ωi . Как видим, рост величины ωкр1Ωi су-

щественно увеличивает задержку сигнала t′ и растягивает его во времени (см. рис. 5.32-5.34).

Теперь рассмотрим распространение в волноводе частотно моду- лированных сигналов 2 и 3 (рис. 5.30, б, в), которые не являются уз- кополосными (рис. 5.29, б). На рис. 5.38, а, в, показаны временные зависимости давления при распространении сигнала 2, а на рис. 5.38, б, г - соответствующие зависимости для сигнала 3 в точках на- блюдения с координатами x′ = 50 (рис. 5.38, а, б) и x′ =150 (рис. 5.38, в, г), z /h = 0,5 при значении критической частоты первой моды

ωкр1Ωi = 60 . Сравнивая эти рисунки можно заметить следующее:

1) наблюдается формирование резкого переднего фронта сигнала 2; при этом, как видно на рис. 5.38, а, в, пиковые значения давления превышают амплитуду давления исходного сигнала 2 в сечении x = 0 более чем в два раза. Расчеты показывают, что пиковые значения давления, которые превышают амплитуду исходного сигнала более чем в два раза, наблюдаются, при выбранных параметрах волновода, на расстояниях x′ ≈ 40...200 ;

284

Рис. 5.38. Временные зависимости давления при распространении сигнала 2 (а, в) и сигнала 3 (б, г) в точке с координатой x′; ωкр1Ωi = 60 , z /h = 0,5 :

а, б - x′ = 50 , в, г - x′ =150

285

2) пространственное “размывание” импульсного сигнала 2 значи- тельно меньше, чем для сигнала 3, при этом на относительно неболь- ших расстояниях x′ можно наблюдать сжатие во времени и про- странстве сигнала 2;

3) скорость распространения переднего фронта сигнала, в кото- ром сосредоточенная основная часть энергии, для сигнала 3 больше, чем сигнала 2.

Объяснение этим особенностям распространения сигналов 2 и 3 можно найти, анализируя частотные зависимости фазовой и группо- вой скоростей первой моды на рис. 5.35. Как видим, с ростом часто- ты первой моды ω (при ω > ωкр1) групповая скорость увеличивается.

Вследствие этого пространственно-временная эволюция сигнала 2, на некотором пути распространения, приводит к его “сжатию” (рис. 5.38, а, в). Понятно, что с увеличением пути распространения сигнала 2 дисперсия, которая по началу привела к его пространственно- временному сжатию, в дальнейшем все ж таки приведет к его “раз- мыванию”. Для сигнала 3 имеем пространственно-временное “размы- вание” сигнала (рис. 5.38, б, г) на протяжении всего пути его распро- странения. Понятно, что при этом скорость переднего фронта сигна- ла 3 будет большей, чем сигнала 2.

Заметим, что эффект формирования резкого переднего фронта в процессе распространения частотно модулированного сигнала, кото- рый сопровождается аномальным ростом его амплитуды, хорошо из- вестен в лазерной оптике и называется дисперсионным фокусирова- нием . Такой термин был введен, чтобы не путать этот эффект с гео- метрическим фокусированием, которое можно обеспечить, например, за счет использования параболического отражателя волн или линзы. Теперь мы можем убедиться, что дисперсионное фокусирование можно наблюдать также и в акустике.

Интересно отметить, что эффекты подобного рода наблюдаются также и при распространении гравитационных волн на морской по- верхности. Неоднократно было зафиксировано, что на поверхности моря внезапно возникают аномально высокие одиночные волны, ко- торые имеют большую разрушительную силу. Такие волны часто на- зывают волнами-убийцами. Известные случаи, когда их столкновенье

сморскими судами приводило к катастрофическим последствиям .

Casperson L.V., Yariv A. Gain and dispersion focusing in a high gain laser

//Appl. Opt. – 1972. – 11, № 2. – P. 462–466.

Пелиновский Е.Н., Слюняев А.В. «Фрики» – морские волны-убийцы //

Природа. – 2007. – № 3. – С. 14–23.

286

5.15.3. Распространение в волноводе импульсного сиг- нала с многомодовой пространственной структурой

Теперь пусть в плоскопараллельном волноводе в сечении x = 0 задано равномерное распределение амплитуды давления на не-

котором отрезке z1,z2 (см. рис. 5.31, б):

а временная зависимость определяется формулой (5.223), т.е. рас- сматриваем сигнал 1.

Представим исходное распределение давления (5.241) в виде ряда Фурье по собственным формам gm (z ) мод плоскопараллельного вол- новода:

ным формулам с использованием свойства ортогональности собст- венных форм gm (z ) на отрезке z = [0,h ].

Рис. 5.39. Значение первых пятидесяти коэффициентов ряда Фурье (5.232): а - акустически мягкий волновод, б - акустически жесткий волновод

Будем считать, что функция (5.241) симметрична относительно плоскости z = h2 волновода, полагая конкретно z1 = 0,45h и

z2 = 0,55h . На рис. 5.39 отображены значения первых пятидесяти

m = 0,2,4,.... Для волновода с акустически жесткими границами (рис. 5.39, б) dm = 0 при m =1,2,3,... . Понятно, что этот факт является

следствием акустических свойств границ волновода и симметрии от- носительно плоскости z = h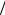2 функции (5.241).

Поле давления в волноводе будет иметь вид двойной суммы, а именно

каждая m -тая собственная форма gm (z ) определяет создание m -ой моды с частотами ωk , k =1,2,... и соответствующими амплитудными

Согласно соотношению (5.244) условие того, что m -тая нормальная волна с частотою ωk будет распространяющейся, примет вид

Итак, будет ли нормальная волна однородной или неоднородной за- висит (при фиксированной величине Nq =100 ) от номера моды m ,

числа k , которое определяет частоту волны ωk = kΩi и волновой ши- рины волновода h′ = hλ0 , ( λ0 = cT0 - длина волны на частоте ω0 ).

Попробуем разобраться в особенностях волноводного распростра- нения сигнала 1, последовательно увеличивая величину волновой ши- рины волновода h′ . Пусть h′ = 0,7 . Введем вспомогательную функ-

цию Gm (k ) = mk 2Nqh′ , которая при заданных величинах m и h′

( Nq =100 ) определяет принадлежность m -той моды к однородной или неоднородной. На рис. 5.40 показаны графики функции Gm (k ), m =1,2,3,4 от аргумента k = ωk /ω1 . Напомним, что непарные моды (m =1,2,...) определяют поле в волноводе с акустически мягкими гра- ницами, а парные (m = 0,2,4,...) – в волноводе с акустически жестки- ми границами. Для нулевой моды (m = 0 ) дисперсия отсутствует, т. к. она является обычной однородной плоской волной на любой частоте.

288

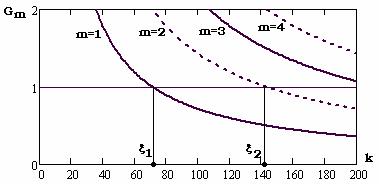
Точка пересечения кривой с прямой на уровне единицы определяет число ξm = ωкрm /ω1 и соответственно критическую частоту m -ой мо-

ды ωкрm . Таким образом волны для которых k > ξm , а значит ωk > ωкрm , будут однородными.

Рис. 5.40. График функции Gm (k ) при величине h′ = 0,7 ; m =1,2,3,4

Напомним, что амплитуда давления m -той моды с частотой ωk определяется произведением dm pk , здесь коэффициенты dm пред-

ставлены на рис. 5.39 и согласно рис. 5.29, а девяносто процентов энергии сигнала 1 сосредоточенно в составляющих с частотами ωk ,

k = 90,91,...,100 .

Анализируя рис. 5.40, можно сделать вывод: в случае волновода с акустически мягкими границами энергонесущими будут первые мо- ды с частотами ωk , k ≥ 72 , (здесь ξ1 ≈ 71,4), а для волновода с аку-

стически жесткими границами фактически вся энергия будет сосре- доточена в нулевой моде ( ξ0 = 0 ) (вторая мода будет однородной

только на частотах ωk , k ≥143 , (здесь ξ2 ≈142,9 )). Как следствие,

звуковые поля в этих волноводах будут существенно отличаться, рис. 5.41. Действительно, если в акустически жестком волноводе диспер- сионные явления практически отсутствуют (рис. 5.41, б), то для аку- стически мягкого волновода (рис. 5.41, а) они проявляются в полной мере.

289

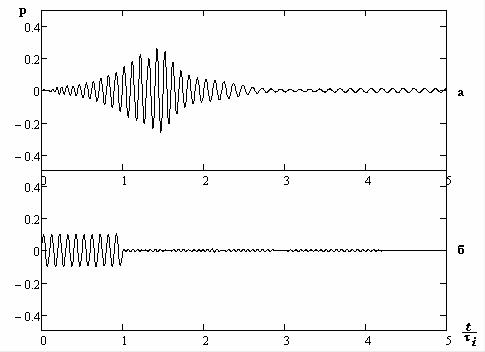
Рис. 5.41. Временная зависимость давления при распространении сигнала

1, h′ = 0,7 , x′ = 20 , z /h = 0,5 :

а - акустически мягкий волновод, б - акустически жесткий волновод

Увеличим размер волновода до величины h′ =1,7 и обратимся к рис. 5.42, где представлены графики функции Gm (k ). Как видим,

теперь волновой процесс далеко от источника возмущения ( x = 0 ) практически формируют две моды: для акустически мягкого волно- вода - первая ( ξ1 ≈ 29,4 ) и третья ( ξ3 ≈ 88,2 ), а для акустически жест-

кого волновода – нулевая ( ξ0 = 0 ) и вторая ( ξ2 ≈ 58,8 ), поскольку ξ4,ξ5 >110 . Поэтому, наряду с эффектом “размывания” сигнала, воз-

можны и более существенные изменения формы импульсного сигна- ла. Иллюстрацией к сказанному являются графики на рис. 5.43. Для акустически мягкого волновода на расстоянии всего x′ =1 (рис. 5.43, а) имеем деструктивную интерференцию волн разных частот первой и третьей моды, а на расстоянии x′ = 7 (рис. 5.43, в) интерференция тех же волн образовывает своеобразный “двойной” импульс. В тоже время в акустически жестком волноводе на указанных расстояниях (рис. 5.43, б, г) удается удержать форму исходного сигнала 1 за счет доминирования нулевой моды.

290