Основы_акустики_Гринченко_Вовк

Всесторонним растяжением (или всестороннее сжатие в зависи- мости от знака деформации) называют деформацию, при которой уд- линение одинаково вдоль всех трех осей, а деформации сдвига отсут- ствуют:

называют модулем всестороннего сжатия или объемным модулем упругости.

Деформация чистого сдвига, скажем, в плоскости х1х2, есть де- формация, при которой отличны от нуля только компоненты u12 = u21 тензора деформаций. Из выражения (6.86) получим

Таким образом, коэффициент Ламе μ представляет собой модуль сдвига G, который определяется при чистом сдвиге из соотношения μ = σ12/(2u12) = G. Понятно, что постоянные Ламе λ и μ имеют размер- ность поверхностных сил.

Теперь рассмотрим однородное растяжение цилиндрического стрежня со свободной боковой поверхностью. Направим ось Ox1 вдоль оси стрежня. Единственной отличной от нуля компонентой на- пряжения будет σ11, поскольку на боковых стенках стрежня напря- жения равны нулю. В этом случае из уравнений (6.86) получим

Уравнения (6.94) и (6.95) выполняются при условии

331

и называют коэффициентом Пуассона. Коэффициент Пуассона свя- зывает деформации в продольном и поперечном направлениях. Знак “минус” в (6.96) характеризует экспериментальный факт: при растя-

жении стрежня в продольном направлении происходит уменьшение его поперечного размера.

Определим физический смысл первого коэффициента Ламе λ. Снова рассмотрим растяжение стрежня вдоль оси Ох1, но при усло- вии, что боковая поверхность стрежня зажата и, следовательно, не- подвижна. В этом случае компоненты тензора деформаций равны ну- лю, кроме u11. Тогда вместо (6.93)-(6.95) следует записать

σ11 = (λ + 2μ)u11 ,

σ22 = λu11, σ33 = λu11.

Таким образом, коэффициент λ = σ22/u11 = σ33/u11 равен отношению поперечного нормального напряжения к деформации стрежня при растяжении стрежня с зажатыми боковыми гранями.

Поскольку в закон Гука для изотропного тела входят только две независимые характеристики вещества, то между модулями упруго- сти λ, μ, К, Е, ν, G может быть только линейная зависимость. Если основными являются постоянные Ламе λ и μ, то

* Юнг (Young) Томас (1773—1829) — английский физик.

332

Все модули упругости положительные (действительно, тела “оказыва- ют сопротивление” деформациям, а не “способствуют” им). При этом выполняются неравенства:

E < 3K , 2μ < E < 3μ , K < λ + 2μ < 3K , 0 < ν < 0,5.

Коэффициент Пуассона, близкий к нулю, имеет пробка: при растяже- нии и сжатии поперечные размеры тела из пробки практически не изменяются. Предельный случай ν → 0,5 соответствует μ → 0, т.е. пе- реходу от твердого тела к жидкости.

В таблице приведены характерные величины для ряда упругих

333

6.6. Общие уравнения распространения волн в твердых телах

Получим линеаризованные уравнения движения для твер- дой изотропной среды. Для этого рассмотрим частицу среды в виде прямоугольного параллелепипеда со сторонами dx1, dx2, dx3. Если бы деформация в среде была однородной, то одноименные компоненты тензора напряжений были бы по модулю одинаковы и, как следствие, частицы оставались бы неподвижными. Однако при неоднородном напряженном состоянии, например в упругой волне, напряжения на противоположных гранях не равны по модулю, что служит причиной движения частицы среды.

Рис. 6.11. Мысленная элементарная частичка среды твердого тела

Рассмотрим компоненту движения вдоль одной из трех осей коор- динат, например оси Ох2 (рис. 6.11). Сила, которая действует по второ- му закону Ньютона, приложена к граням элементарного параллелепи- педа из окружающей среды. Она выражается через механические напряжения на гранях параллелепипеда. На рис. 6.11 показаны про- екции напряжения на ось Ох2. Запишем проекцию силы на ось Ох2:

dF2 = (σ12′ − σ12 )dx2dx3 + (σ′22 − σ22 )dx1dx3 + (σ32′ − σ32 )dx1dx2 . По-

скольку σ12′ (x1 + dx1,x2,x3 ) , σ′22(x1,x2 + dx2,x3 ), σ′32(x1,x2,x3 + dx3 ), то,

применяя формулу Лагранжа о приращении функции при малом из- менении аргумента, получаем

Под действием этой силы частичка будет двигаться вдоль оси Ох2 с ускорением ∂2u2/∂t 2, где u2 проекция на ось Ox2 вектора смещения u = (u1, u2, u3) частицы. Масса частицы равна ρdx1dx2dx3, где ρ — плотность среды. Итак, уравнение движения частицы вдоль оси Ox2

имеет вид ∂σi2 = ρ ∂2u2 . Рассматривая аналогично движение частицы

∂xi ∂t2

вдоль других осей координат, получаем систему из трех уравнений:

334

Это и есть уравнения движения (для ускорения использована частная производная ∂ 2/∂t 2 вместо d 2/dt 2, что обусловлено пренебрежением ускорения переноса (см. п. 4.1.2)).

Уравнение (6.105) связывают две функции координат и времени: тензор напряжений σik (x1,x2,x3,t ) и вектор смещения u(x1,x2,x3,t). Для того чтобы число уравнений соответствовало числу неизвестных функций, необходимо иметь еще одно уравнение, которое связывает σik и u. Таким уравнением является обобщенный закон Гука

(см. (6.86)):

Подстановка (6.106) в (6.105) позволяет получить уравнение относи- тельно проекций вектора u:

Умножим каждое из трех уравнений (6.108) на соответствующий ба- зисный вектор ej, j = 1,2,3, и просуммируем. Поскольку e1 ∂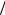∂x1 + e2 ∂∂x2 +e3 ∂∂x3 ≡ grad , то искомое уравнение запишем в

виде

335

При решении конкретных задач часто используют другую форму урав- нения движения. Учитывая тождество u = graddivu — rotrotu, пере- писываем (6.109) так:

Известно [8, 52], что любое векторное поле можно представить в виде суммы потенциального (от латинского слова potentia — сила) вектора, ротор которого равен нулю, и соленоидального (от греческого слова swlhu (солен) — трубка) вектора, дивергенция которого равна нулю. Если записать в таком виде вектор смещения u, то можно по- лучить отдельно уравнение потенциальной и соленоидальной частей смещения. Действительно, пусть u = ue + ut, считая rotue = 0 и divut = 0; подставляя в (6.110), получаем

Поскольку разложение вектора на потенциальную и соленоидальную части является единственным, то согласно (6.111) имеем

Подставляя (6.114), (6.115) в (6.112), (6.113) получаем волновые урав- нения для ue и ut :

Для гармонических волн, т.е. при временной зависимости exp(–iωt), уравнения (6.116) превращаются у уравнения Гельмгольца:

336

где ke = ω/ce, kt = ω/ct — волновые числа соответственно для ue и ut.

6.7. Продольные и поперечные волны

В пятом разделе мы исследовали решение волнового урав- нения в виде плоской продольной волны в идеальной сжимаемой жидкости. Рассмотрим теперь, что представляют собой плоские вол- ны ue и ut в твердом теле, как решение уравнений (6.116). Очевидно постоянные ce и ct (см. (6.115)) в волновых уравнениях (6.116) имеют смысл скорости распространения волн. Рассмотрим плоские гармо- нические волны, которые распространяются вдоль оси Ох1 декарто- вой системы координат:

где A(e) = e1A1(e) + e2A2(e) + e3A3(e) и A(t ) = e1A1(t) + e2A2(t ) + e3A3(t ) — векторы

амплитуд.

Определим характер колебаний частиц среды в этих волнах, опи- раясь на основные свойства векторов ue (rotue = 0) и ut (divut = 0). Ис- пользуя (6.118), вычисляем rotue и записываем уравнение

Отсюда имеем A3(e) = 0, A2(e) = 0. Итак, вектор ue, направлен вдоль оси

Ox1, т.е. движение частиц среды происходит в направлении распро- странения волны. Таким образом, волна ue(x1, x2, x3, t) является про- дольной волной.

Используя (6.119), вычисляем divut и записываем уравнение

A(t ) iω exp[−iω(t − x ct )] = 0.

1 ct

Отсюда имеем A1(t) = 0. Итак, вектор ut ориентирован перпендикуляр-

но к направлению распространения волны (оси Ох1). Таким образом, волна ut(x1, x2, x3, t) является поперечной волной. Поскольку в попе- речной волне частицы среды двигаются в плоскости, перпендикуляр- ной к направлению распространения волны, то возникает вопрос о характере движения частиц в этой плоскости. Это свойство называ-

ют поляризацией поперечной волны.

Пусть ось Ох3 декартовой системы координат совпадает с направ- лением волнового вектора поперечной волны. Тогда произвольное смещение частиц u в такой волне можно представить в виде суммы

337

двух взаимно ортогональных векторов u1, u2, направленных вдоль осей соответственно Ox1 и Ox2. При этом возможны ситуации, кото- рые показаны на рис. 6.12.

Рис. 6.12. Формы поляризации поперечной волны

Если u1 = 0, то имеем волну, в которой смещение лежит в плоско- сти х2Ох3 и изменяется по закону (рис. 6.12, а):

Выражение (6.120) определяет линейно поляризованную волну. Аналогично определяется линейно поляризованная волна, смеще-

ние частиц которой лежит в плоскости х1Ох3 (рис. 6.12, б) и задается выражением

Произвольная линейная комбинация выражений (6.120) и (6.121) также определяет волну, которая поляризована в плоскости х1Ох2. Ес- ли взять суперпозицию движений (6.120) и (6.121) с произвольным сдвигом фаз α, то получим движение в виде

(рис. 6.12, в); имеем поперечную волну с эллиптической поляризаци- ей. В частном случае А2 = А1, α = ±π/2 получим поперечную волну с круговой поляризацией (рис. 6.12, г).

Согласно (6.118) и (6.119) продольные и поперечные волны рас- пространяются с фазовыми скоростями соответственно ce и ct. Из формул (6.115) видно, что скорость продольных волн всегда больше

338

скорости поперечных. В конце параграфа 6.5 в таблице указаны величины скоростей ce и ct для некоторых веществ.

Целесообразно привести ряд формул, которые определяют ce и ct через различные упругие постоянные:

Отсюда между скоростями продольной и поперечной волн существует такая связь:

Это отношение для разных металлов изменяется довольно существен- но, например, для цинка (ν ≈ 0,25) и свинца (ν ≈ 0,44) отношение ско- ростей, вычисленное по (6.125), определяется числами 1,73 и 3,3.

В конце параграфа сделаем важный вывод. Как видим, уравнение движения (6.111) можно заменить двумя волновыми уравнениями (6.116). Решение первого представляет собой продольную волну, а решение второго — поперечную. Таким образом, произвольная пло- ская волна в упругой изотропной среде может быть представлена в виде суперпозиции продольной и поперечной волн, каждая из кото- рых распространяется со своей фазовой скоростью. Определить фа- зовую скорость для волнового движения в виде суперпозиции этих волн невозможно. В сущности, здесь имеем два волновые движения, которые не взаимодействуют друг с другом.

6.8. Граничные условия для твердых тел

Очень важным моментом с точки зрения, как усложнения волновой картины, так и возможности практического использования результатов исследования, есть наличие границы в волновых задачах. Введение границы S упругого тела и постановки условий на ее по- верхности, по сути, является моделированием процессов взаимодей- ствия упругих тел между собой. В некоторых случаях существенное от- личие в физико-механических свойствах взаимодействующих тел по- зволяет говорить о свободной или закрепленной границе. Вообще вы- бор правильной модели для описания процессов динамического взаи- модействия упругих тел представляет собой очень сложную задачу. Сама граница упругого тела в геометрическом смысле рассматривает- ся как поверхность. На такой поверхности считается возможным за-

339

давать разные условия для компонентов тензора напряжений, вектора смещения или их комбинаций.

Рассмотрим важные модели граничных условий на границе твер- дого тела с другими телами или с вакуумом; разнообразие здесь большее, чем для жидкостей. Будем обозначать ось, которая совпада- ет с нормалью к границе, индексом n, а две взаимно перпендикуляр- ные оси в плоскости границы — индексом α, α = 1,2.

1. Свободная граница. Компоненты тензора напряжений: равны

нулю σnn = σnα = 0.

2. Граница с абсолютно жестким телом при наличии “склеива-

ния”. Все компоненты смещения точек границы равны нулю:

un = uα = 0.

3. Граница с абсолютно жестким телом при наличии “ смазки”.

Нормальное смещение точек границы и касательные напряжения на границе равны нулю: un = 0, σnα = 0.

4. Граница с жидкостью. Нормальное напряжение на границе рав- но давлению в жидкости, взятому с противоположным знаком; каса- тельные напряжения равны нулю; нормальные скорости частиц твердого тела и жидкости на границе равны между собой:

σnn = –p, σnα = 0, ∂un = υn .

∂t

5. Граница с другим твердым телом при наличии “ склеивания”.

Все компоненты смещения обоих тел на границе и одноименные ком- поненты тензора напряжения попарно равны: ui(I) = ui(II), i = 1,2,3;

σnn(I) = σnn(II), σn(I)α = σn(II)α .

6. Граница с другим твердым телом при наличии “ смазки”. По-

парно нормальные смещения и нормальные напряжения обоих тел на границе равны; касательные напряжения в обоих телах равны нулю:

un(I) = un(II), σnn(I) = σnn(II), σn(I)α = σn(II)α = 0.

6.9. Отражение плоской гармонической волны от свободной границы полупространства

Рассматривая волновое движение в однородном бесконеч- ном пространстве, мы поняли очень важную вещь: любое волновое движение в твердом теле всегда можно представить в виде суперпо- зиции продольных и поперечных волн. Наличие двух типов волновых движений в твердом теле значительно усложняет решение конкрет- ных волновых задач по сравнению с подобной ситуацией для акусти- ческих волн в жидкой среде. Ярким и очень важным примером явля- ется задача падения плоской упругой волны на плоскую границу раз-

340