Операторы физических величин

2.5. Чистые и смешанные состояния.

2.5. Чистые и смешанные состояния.

Любые собственные значения эрмитова оператора физической величины

– это и есть те значения этой физической величины, которые могут быть получены в эксперименте.

Соответствующая данному собственному значению собственная функция описывает такое состояние системы, в котором физическая величина принимает значение, равное данному собственному значению.

В таком состоянии собственное значение равно an, а описывается это состояние собственной функцией Yn. Состояние называется чистым.

Возможна и другая ситуация. В процессе измерения в эксперименте возникают значения физической величины, равные различным собственным значениям. Например, с1 и с2. Волновая функция системы в данном

состоянии

где j1 и j2 – собственные функции, соответствующие собственному значению с1 и с2. Описывается это состояние собственной функцией Y. В

этом случае состояние называется смешанным. Разумеется, число слагаемых в линейной комбинации (1) может быть любым, даже бесконечно большим.

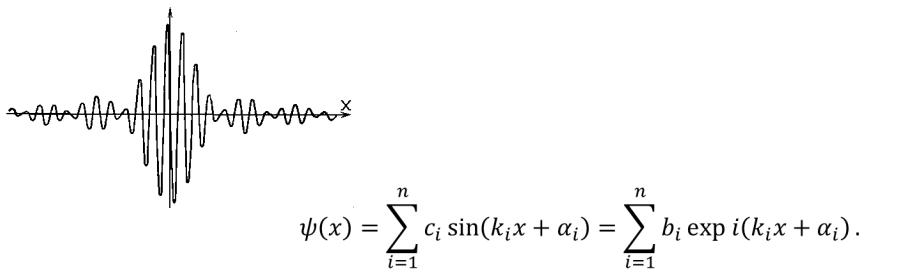
2.5. Чистые и смешанные состояния.

Любой оператор физической величины имеет набор собственных функций. Так, собственными функциями оператора импульса являются плоские волны. Всякая плоская волна (волна де Бройля) соответствует определенному значению импульса частицы.

Но, согласно требованию локализации частицы вблизи некоторой точки, мы должны поставить в соответствие частице не плоскую волну, а волновой пакет, т.е. суперпозицию большого числа плоских волн.

Математически зависимость амплитуды волнового пакета от координаты можно представить в виде ряда Фурье, или как суперпозицию большого числа плоских волн:

2.5. Чистые и смешанные состояния.

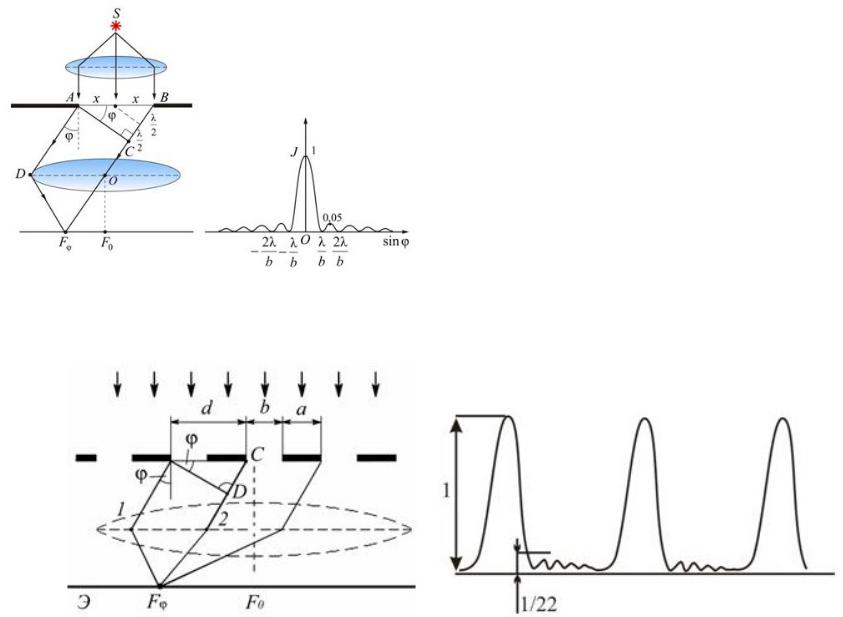
Примером суперпозиции состояний с различными значениями может служить и дифракционный опыт Дэвиссона и Джермера. После взаимодействия с кристаллом (или со щелью) движение частиц можно представить целой совокупностью волн де Бройля, отличающихся друг от друга направлением распространения. Эти явления есть частное выражение общего принципа суперпозиции состояний.

2.5. Чистые и смешанные состояния.

Если система способна находиться в состоянии, изображаемом волновой функцией j1 и в другом состоянии, изображаемом волновой функцией j2, то

она может находиться и в состоянии, изображаемом волновой функцией

Отсюда следует, что если j1, j2, ..., jn - собственные функции

некоторого оператора физической величины, то существует такое сложное состояние, для которого

Отсюда также следует вывод, что всякое состояние можно рассматривать, как суперпозицию волн де Бройля, т.е. состояний с определенными значениями импульса.

Рассмотрим подробнее результаты опытов по дифракции электронов с этой точки зрения. Дифракция на тот или иной угол jm означает, что мы

имеем дело с волнами разной длины:

2.5. Чистые и смешанные состояния.

Согласно формуле де Бройля

следовательно, можно говорить о дифракции электронов, обладающих разными импульсами

Разумеется, каждый электрон, падающий на щель, отклоняется на вполне конкретный угол jm, и, следовательно, обладает вполне конкретным

значением импульса pm.

В то же время, каждый акт дифракции можно рассматривать, как измерение импульса электрона. В процессе измерений могут быть получены разнообразные значения импульса. Вероятность получения одних больше, других – меньше.

2.5. Чистые и смешанные состояния.

То есть можно считать, что электрон, падающий на щель, находился в смешанном состоянии, описываемом волновой функцией

где jn – волновые функции в состояниях с импульсом pn; cn –коэффициенты.

Значения этих коэффициентов тем больше, чем более вероятно обнаружить электрон с соответствующим значением импульса.

Операторы физических величин

2.6. Среднее значение физической величины

2.6. Среднее значение физической величины.

Среднее значение некоторой физической величины A можно определить по формуле

где А – оператор этой физической величины, а интеграл берётся по всей области определения волновой функции Ψ(x).

Доказательство. Пусть в эксперименте по измерению некоторой физической величины появляются её значения a1, a2, …, an. При этом

значение a1 было получено b1 раз, значение a2 – b2 раз, значение an – bn раз. В этом случае среднее значение физической величины равно

где N – общее число измерений. Величина

есть вероятность появления в эксперименте значения физической величинв, равного ai.

2.6. Среднее значение физической величины.

Формулу для среднего значения физической величины можно переписать так:

Ранее мы показали, что любую волновую функцию можно представить в виде ряда по собственным функциям оператора некоторой физической величины, в том числе и величины А:

Коэффициенты bi определяют «вес» состояния с определённым значением ai

физической величины А в волновой функции Y рассматриваемого

произвольного состояния. Коэффициенты bi можно найти как

Квадраты модулей коэффициентов bi равны вероятности обнаружить в

эксперименте то собственное значение величины А, которое соответствует собственной функции ji.