2.2.3. Эрмитово сопряжённые (эрмитовы) операторы.
Линейные операторы, удовлетворяющие свойству
называются самосопряжёнными, эрмитово сопряжёнными или эрмитовыми.
2.2.3. Свойства эрмитовых операторов.
Ортогональность набора собственных функций эрмитова оператора.
Теорема. Любые две собственные функции любого эрмитова оператора удовлетворяют условию
где c – константа, а собственное значение эрмитова оператора действительны.
Доказательство: f m и f n – собственные функции оператора А, поэтому
Для функции, комплексно сопряжённой к fm также выполняется условие
оператор эрмитов. Согласно определению эрмитова оператора, это означает, что
Подействуем оператором А на функцию в левой и правой части последней формулы.
2.2.3. Свойства эрмитовых операторов.
Ортогональность набора собственных функций эрмитова оператора.
Левая часть:
Правая часть:
После подстановки этих выражений в определение эрмитова оператора получаем:
и am – константы, поэтому
Вынося за знак интеграла константы, получим:
При m = n получаем
2.2.3. Свойства эрмитовых операторов.
Ортогональность набора собственных функций эрмитова оператора.
Интеграл в этой формуле не равен нулю, более того, он действителен, следовательно
Последнее равенство может быть справедливым лишь в случае, когда am
действительно. Таким образом, собственные значения эрмитова оператора
действительны.
Вернёмся к рассмотрению формулы
1) Если |
то |
2) Если |
то |
Таким образом, |
|
Собственные функции эрмитова оператора образуют ортогональный набор функций.
2.2.3. Свойства эрмитовых операторов.
Можно потребовать (и легко добиться) того, чтобы с = 1. Тогда
В этом случае собственные функции эрмитова оператора образуют ортонормированный набор функций.
Для того, чтобы условие ортогональности собственных функций выполнялось в виде (1) необходимо, чтобы для самих функций выполнялось условие нормировки
Добиться выполнения этого условия можно с помощью множителей, на которые следует умножать собственные функции. Такие множители называются нормировочными множителями.
В случае, когда одному собственному значению соответствует две или более собственные функции эрмитова оператора, можно выбрать линейные комбинации собственных функций, которые будут ортогональны друг другу.
2.2.3. Свойства эрмитовых операторов.
Полнота набора собственных функций эрмитова оператора.
Важное свойство бесконечного набора собственных функций эрмитова оператора состоит в том, что по ним можно разложить некоторую функцию Y(x), то есть представит её в виде
Существуют определённые ограничения на вид функций Y(x), в частности, на их поведение на бесконечности, но будем считать, что все функции, рассматриваемые в квантовой механике «хорошие», то есть удовлетворяют этим ограничениям.
Коэффициенты разложения bn функции Y(x) можно найти следующим
образом.
Функцию Y(x) умножим на и проинтегрируем по всей области определения:
2.2.3. Свойства эрмитовых операторов.
Полнота набора собственных функций эрмитова оператора.
Таким образом, коэффициенты разложения bi функции Y(x) равны:
2.Основные постулаты квантовой механики.
2.3.Волновые функции. Операторы физических величин
2.3.1. Волновая функция и её вероятностная интерпретация.
Описание микрообъектов, обладающих корпускулярными и волновыми свойствами, будем проводить с помощью волновых функций. В общем случае волновая функция может зависеть от координат и времени.
Волновая функция содержит всю динамическую информацию о системе.
Физический смысл волновой функции. Квадрат модуля волновой функции равен амплитуде вероятности обнаружить частицу в данный момент времени в данной точке пространства (в малой окрестности точки x +Δx, y +Δy, z +Δz, в промежуток времени t +Δt).
Вероятностная интерпретация волновой функции предопределяет её
свойства.
1.Волновая функция – в общем случае – комплексная функция координат
ивремени.
2.Волновая функция однозначна.
В противном случае вероятность обнаружить частицу в некоторой точке не определена.
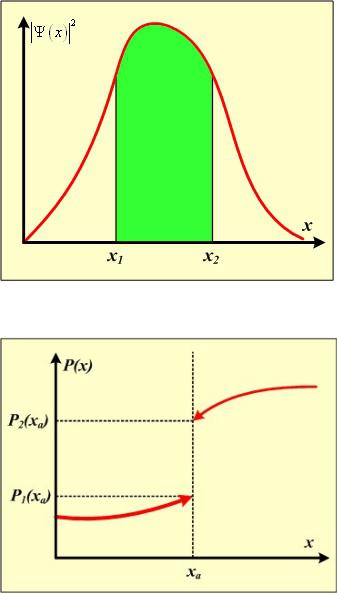
2.3.1. Волновая функция и её вероятностная интерпретация.
3. Вероятность обнаружить частицу с координатой в интервале от x1 до x2 равна
Квадрат модуля волновой функции должен быть интегрируемой функцией.
4. Волновая функция непрерывна вместе со своими производными.
Если бы волновая функция претерпевала разрыв, вероятность обнаружить частицу в точке с координатой xa была бы разной при
приближении к этой точке справа и слева.