6. 3 Выпуклость, вогнутость, точки перегиба. Асимптоты.

Функция называетсявыпуклой (вогнутой) на интервале , если её график лежит под касательной (над касательной), проведённой к графику данной функции, в любой точке интервала.

Иногда выпуклость называют выпуклостью вверх, а вогнутость – выпуклостью вниз.

Если функция дважды дифференцируема на интервалеи() при всех, то функция является вогнутой (выпуклой) на.

Точка , принадлежащая области определенияфункции, называетсяточкой перегиба функции, если при переходе через неё меняется направление выпуклости функции. Точка при этом называетсяточкой перегиба графика функции.

Точка называетсяточкой возможного перегиба функции , если в этой точкеилине существует. Эти точки разбивают область определенияфункциина интервалы выпуклости и вогнутости.

Необходимое условие перегиба. Если - точка перегиба функции, тоилине существует.

Достаточное условие перегиба. Пусть функция дважды дифференцируема в окрестности точки, в которойилине существует. Тогда, если производная, при переходе через точкуменяет знак, то- точка перегиба.

В задачах 5.281-5.292 найти точки перегиба и интервалы вогнутости и выпуклости графиков данных функций:

5.281 5.282

5.283 5.284

5.285 5.286

5.287 5.288

5.289 5.290

5.291 5.292

Прямая называется асимптотой графикафункции, если расстояние от точкидо прямойстремится к нулю при бесконечном удалении точкиот начала координат.

Прямая называетсявертикальной асимптотой графика функции , если хотя бы один из односторонних пределовилиравен бесконечности.

Прямая является вертикальной асимптотой, тогда и только тогда, когдаявляется точкой бесконечного разрыва функции. Непрерывные функции не имеют вертикальных асимптот.

Прямая называетсянаклонной асимптотой графика функции при(при), если(соответственно,). Частным случаем наклонной асимптоты (при) являетсягоризонтальная асимптота.

Прямая являетсянаклонной асимптотой графика функции при(при) тогда и только тогда, когда одновременно существуют пределы:и(соответственно,и).

В задачах 5.293-5.308 найти асимптоты графиков функций:

5.293 5.294

5.295 5.296

5.297 5.298

5.299 5.300

5.301 5.302

5.303 5.304

5.305 5.306

5.307 5.308

6.4 Построение графиков функций.

Для построения графика функции нужно:1) найти область определения функции; 2) найти область непрерывности функции и точки разрыва; 3) исследовать функцию на чётность, нечётность и периодичность; 4) найти точки пересечения графика с осями координат; 5) найти асимптоты графика функции; 6) найти интервалы возрастания и убывания, экстремумы функции; 7) найти интервалы выпуклости, вогнутости и точки перегиба.

В задачах 5.309-5.345 провести полное исследование следующих функций и построить их графики:

5.309 А); б); в).

5.310 а); б); в).

5.311а); б); в).

5.312а); б); в).

5.313а); б); в).

5.314а); б); в).

5.315а); б); в).

5.316а); б); в).

5.317а); б); в).

5.318а); б); в).

5.319а); б); в).

5.320а); б); в).

5.321а); б); в).

5.322а); б); в).

5.323а); б); в).

5.324а); б); в).

5.325а); б); в).

5.326а); б); в).

5.327а); б); в).

5.328а); б); в).

5.329а); б); в).

5.330а); б); в).

5.331а); б); в).

5.332а); б); в).

5.333а); б); в).

5.334а); б); в).

5.335а); б); в).

5.336а); б); в).

5.337а); б); в).

5.338а); б); в).

5.339а); б); в).

5.340а); б); в).

5.341а); б); в). 5.342а); б); в).

5.343а); б); в).

5.344 а); б); в).

5.345 а); б); в).

§7. Векторные функции действительной переменной.

Если каждому значению действительной переменной поставлен в соответствие вектор, то говорят , что на множествезаданавектор-функция действительной переменной. Заданиевектор-функции равносильно заданию трёх числовых функций- координат вектора:, или, кратко,.

Если вектор является радиус-вектором точки, то его обозначают.Годографом вектор-функции называется линия, описываемая в пространстве концом вектора. Всякую линию в пространстве можно рассматривать как годограф некоторой вектор-функции. Параметрические уравнения годографа:,,.

Производной вектор-функции по аргументуназывается вектор-функция. Если, то. Вектор-функция имеющая производную в данной точке, называетсядифференцируемой в этой точке. Производная есть вектор, направленный по касательной к годографу вектор-функции.

Основные правила дифференцирования вектор-функций.

Если идифференцируемые вектор-функции,- постоянный вектор,- постоянный скаляр,- скалярная функция, то:

Уравнение касательной к пространственной кривой ,,в точке, которой соответствует значение параметра, имеет вид:, ауравнение нормальной плоскости в той же точке – вид:

.

Кривизной кривой в точке называется число, где- угол поворота касательной, соответствующий дугеданной кривой, а- длина этой дуги.

Кривизна плоской кривой вычисляется по формулеи по формуле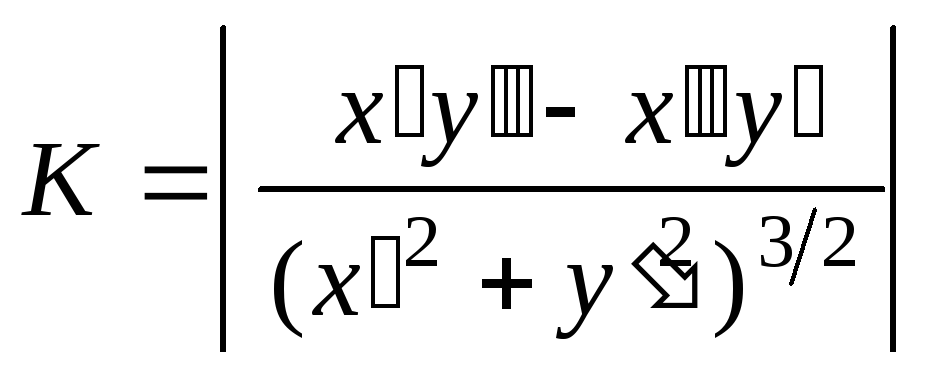, если кривая задана в параметрическом виде уравнениями,.

Величина называетсярадиусом кривизны.

5.346. Найти единичный касательный вектор годографа вектор-функции при:

а),; б),.

5.347. Найти производные вектор-функций :

а); б);

в); г).

5.348. Найти производные вектор-функций при:

а) ,;

б) ,.

5.349. Для каждой из следующих кривых написать уравнения касательной и нормальной плоскости в данной точке:

а) при;

б) при.

5.350. Вычислить радиус кривизны кривых в данной точке:

а) ,; б) , ;

в) , ; г) , ;

д) , ; е) , .

5.351. Вычислить радиус кривизны кривых в данной точке:

а),;б),;

в),;г),