
с течением времени стремится к нулю и может быть вычислена с помощью обратного преобразования Фурье, которое в этом случае принимает вид
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
w(t) |
|
Ф( jω)ejωtdω. |
(10.29) |
||||||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2π |
|
|
|
|||||
Представим |
Ф( jω) и |
ejωt |
через вещественные и |
мнимые |
||||||||||||
частотные характеристики |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
Ф( jω) P(ω) jQ(ω); |
|
||||||||
Тогда |
|
|
|
ejωt cosωt jsinωt. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
w(t) |
|
|
|
[P(ω) jQ(ω)](cosωt jsinωt)dω |
|
|||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
1 |
|
|
|
|
|||||||
|
|
|
|
P(ω)cosωtdω j |
|
|
|
|
P(ω)sinωtdω |
|
||||||
2 |
2 |
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
|
1 |
|
|
|
||||||||
j |
|
|
|
|
Q(ω)cosωtdω |
|
|
Q(ω)sinωtdω. |
|
|||||||
|
|
|
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|||||||
Так как вещественная частотная характеристика есть функция четная P(ω) P( ω), а мнимая – нечетная Q(ω) Q( ω), то получим
1 |
|
|
|
|
|
|
1 |
|
|||||||
|
|
|
|
P(ω)cosωtdω |
|
|
|
|
P(ω)cosωtdω; |
||||||
|
2 |
|
|
||||||||||||
|
|
|
|
|
|
0 |
|
||||||||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
P(ω)sinωtdω 0; |
|||||||
|
|
|
|
|
|
|
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
Q(ω)sinωtdω 0; |
|||||||
|
|
|
|
|
|
|
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
1 |
|
|||||||
|
|
|
|
Q(ω)sinωtdω |
|
|
Q(ω)sinωtdω. |
||||||||
|
|
2 |
|
||||||||||||
|
|
|
|
|
|
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|||
w(t) |
|
P(ω)cosωtdω |
|
|
Q(ω)sinωtdω. |
||||||||||
π |
|
|
|||||||||||||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
231

Так как при t 0 |
w(t) 0, а sinωt sin( ωt), то |
||||||||||
|
|
|
1 |
|
|
|
1 |
||||
w( t) |
|
|
P(ω)cosωtdω |
|
|
Q(ω)sinωtdω 0 |
|||||
π |
π |
||||||||||
|
|
|
0 |
|
|
|
0 |
||||
и |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
1 |
|
|
|
1 |
|
|||||
|
|
P(ω)cosωtdω |
|
|
Q(ω)sinωtdω. |
||||||
|
π |
π |
|||||||||
|
0 |
|
|
|
0 |
|
|
||||
|
|
|
|
|
|
|
|
|
|||
Тогда в окончательном виде получим
2
w(t) P(ω)cosωtdω (10.30) π 0
или эквивалентное соотношение
|
|
|
|
2 |
|
|||||
w(t) |
|
|
Q(ω)sinωtdω. |
(10.31) |
||||||
π |
||||||||||
|
|
|
|
0 |
|
|
|
|||
Учитывая, что |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
dh(t) |
|
|
||
|
|
w(t) |
, |
|
||||||
|
|
|
|
|||||||
получим |
|
|
|
|
|
|
dt |
|
||
|
|
|
|
|
|
|
|
|
||
t |
|
2 |
|
|
|
|
|
|
||
h(t) |
|
|
|
P(ω)cosωtdω dt. |
|
|||||
|
|
|
|
|||||||
0 |
π 0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|||||
Меняя порядок интегрирования и учитывая, что
cosωtdt 1 sinωt,
ω
получим выражение для вычисления переходной функции по вещественной частотной характеристике
|
2 P(ω) |
|
|||
h(t) |
|
|
|
sinωtdω. |
(10.32) |
π |
|
||||
|
0 |
ω |
|
||
|
|
|
|
|
|
Точное определение переходной характеристики по последнему выражению достаточно сложно, но путем аппроксимации вещественной характеристики кусочно-линейной функцией можно получить достаточно удобные выражения для приближенного построения переходной характеристики.
232
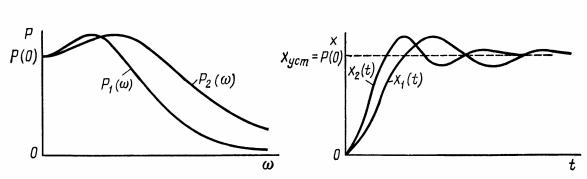
10.3.2. Основные свойства вещественных частотных характеристик. Рассмотрим основные свойства вещественных частотных характеристик и соответствующих им переходных процессов. Из (10.32) следуют основные свойства P(ω) и h(t).
Приведем их без доказательств. |
|
|
|
||
1. Свойство линейности: |
если вещественную частотную |
||||
характеристику можно представить суммой |
|||||
|
n |
|
|
|
|
P(ω) Pi(ω); |
|
||||
|
i 1 |
|
|
(10.33) |
|
|
2 P(ω) |
||||
|
|
||||
|
|
i |
|
||
hi(t) |
|
|
|
|
sinωtdω, |
|
ω |
||||
|
0 |
|
|||
то и переходной процесс h(t) может быть представлен суммой составляющих
n |
|
h(t) hi(t). |
(10.34) |
i1
2.Соответствие масштабов по оси ординат для P(ω) и h(t).
Если умножить P(ω) на постоянный множитель a, то соответствующие значения h(t) тоже умножаются на этот множитель a.
3. Соответствие масштабов по оси абсцисс для P(ω) и h(t). Если аргумент ω в соответствующем выражении частотной характеристики умножить на постоянное число, то аргумент t в соответствующем выражении переходного процесса будет делиться на это число (рис. 10.9, б), т. е.
|
2 P(aω) |
|
||||
h(t/a) |
|
|
|
|
sinωtdω. |
(10.35) |
|
|
|||||
|
0 |
ω |
|
|||
|
|
|
|
|
|
|
а |
б |
Рис. 10.9
233
4. Начальное значение вещественной частотной характеристики равно конечному значению переходной характеристики
lim P(ω) P(0) lim h(t) h( ). |
(10.36) |
|
ω 0 |
t |
|
5. Конечное значение вещественной частотной характеристики равно начальному значению оригинала переходной характеристики
lim |
P(ω) P( ) lim h(t) h(0). |
(10.37) |
|||
ω |
|
t 0 |
|
|
|
6. Представляют |
интерес |
разрывы |
непрерывности |
и |
пики |
в вещественной частотной характеристике. |
|
|
|
||
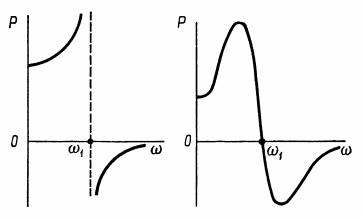
Предположим, |
что при |
ω ω1 |
вещественная |
частотная |
|
характеристика имеет разрыв |
непрерывности P(ω) , |
при |
этом |
||
характеристическое уравнение системы будет иметь мнимый корень s jω1, т. е. в системе устанавливаются незатухающие гармонические колебания, если остальные корни левые. Характеристика для этого случая показана на рис. 10.10, а.
а |
б |
|
Рис. 10.10 |
По-видимому, высокий и острый пик частотной характеристики, за которым P(ω) переходит через нуль, при частоте, близкой к ω1, соответствует медленно затухающим колебаниям (см. рис. 10.9, б)
7. Чтобы переходная характеристика системы имела перерегулирование, не превышающее 18% (σ 18%), вещественная
частотная |
характеристика |
должна |
быть |
положительной |
||
невозрастающей |
функцией |
частоты |
(рис. |
10.11), |
т. е. |
|
P(ω) 0,[dP(ω)/dω] 0. |
|
|
|
|
||
234
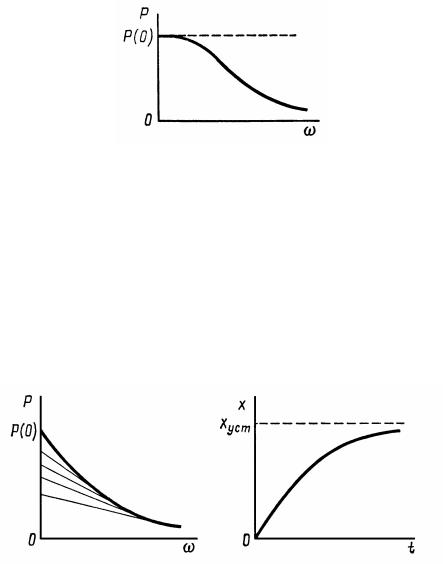
Рис. 10.11
8. Условия монотонного протекания переходного процесса. Чтобы переходной процесс имел монотонный характер, достаточно, чтобы соответствующая ему вещественная частотная характеристика P(ω) являлась положительной, непрерывной функцией частоты с отрицательной, убывающей по абсолютной величине производной
(рис. 10.12, а), т. е. P(ω) 0, dP(ω)/dω 0.
а |
б |
Рис. 10.12
9. Определение наибольшего значения перерегулирования σmax переходного процесса по максимуму вещественной частотной характеристики P(ω) (рис. 10.13)
σmax 1,18Pmax P(0)/P(0) , |
(10.38) |
где Pmax – максимальное значение P(ω); P(0) – начальное значение
P(ω).
10. Если |
вещественная |
частотная характеристика близка |
|
к трапецеидальной, т. е. может быть аппроксимирована |
трапецией |
||
с диапазоном |
частот ω2 и |
коэффициентом наклона |
χ ω1 /ω2 |
235
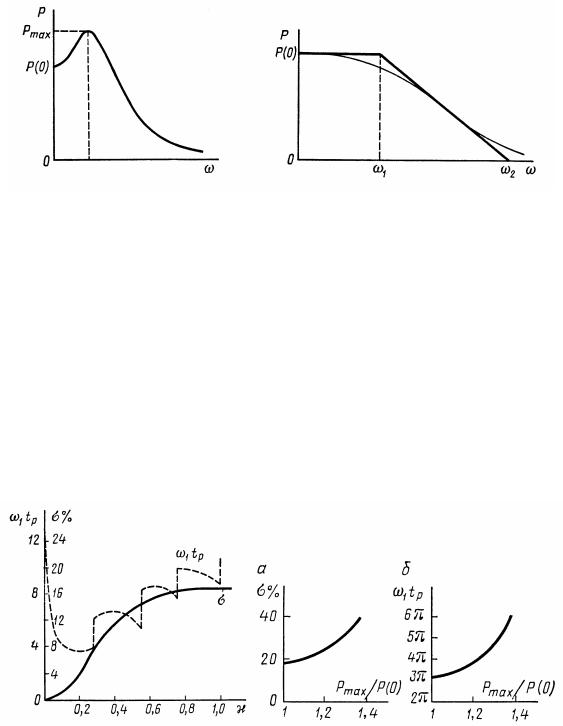
(рис. 10.14), то время регулирования переходного процесса системы заключено в пределах π/ω2 tp 4π/ω2.
Рис. 10.13 |
Рис.10.14 |
Оценить время регулирования tр |
и перерегулирование σ можно |
по кривым, приведенным на (рис. 10.15). Это применимо для систем с невозрастающей вещественной частотной характеристикой.
Если |
вещественная частотная характеристика P(ω) имеет |
||||
максимум |
Pmax , то перерегулирование σ и время регулирования |
||||
оценивают по |
кривым, приведенным на |
рис. |
10.16, а |
и б |
|
в зависимости |
от отношения Pmax /P(0). |
При |
этом |
время |
|
регулирования заключено в пределах 3π/ω2 tp 8π/ω2. |
|
||||
Рис. 10.15 Рис. 10.16
236
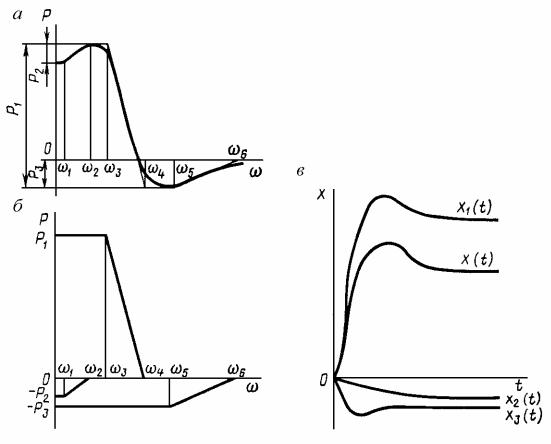
Пример 10.3. Рассмотрим построение переходного процесса по вещественной частотной характеристике.
Решение. Пусть вещественная частотная характеристика имеет вид, показанный на рис. 10.17, а. Аппроксимируем ее ломаной линией и разобьем на три трапеции (рис. 10.17, б). Трапеции 1, 2 и 3 характеризуются соответственно величинами:
P(0) |
P1; |
ω0 ω4; |
ωd ω3; |
P(0) |
P4; |
ω0 ω6; |
ωd ω5; |
P(0) |
P2; |
ω0 ω2; |
ωd ω1. |
Здесь ω0 – частота основания трапеции; ωd – частота точки излома.
Для каждой трапеции найдем переходные процессы h1(t),h2(t), h3(t), приведенные на рис. 10.17, в. Суммируя их, получим искомый переходный процесс h(t).
Рис. 10.17
237
Контрольные вопросы
1.Как можно определить степень устойчивости?
2.Что называют колебательностью системы?
3.Для систем какого порядка используется диаграмма Вышнеградского, что она определяет?
4.Что такое ошибка системы, как она определяется?
5.Какие свойства системы определяют интегральные оценки?
6.Для каких переходных процессов используются квадратичные интегральные оценки?
7.Что такое улучшенные квадратичные интегральные оценки?
8.Какая зависимость существует между переходной функцией и частотными характеристиками системы?
9.Перечислите основные свойства вещественных частотных характеристик.
10.Какое условие должно выполняться при монотонном протекании переходного процесса?
11.В чем заключается приближенный метод построения переходных процессов?
238
