

Следовательно, степень устойчивости |α| 1/2; колебатель-
ность |β/α| 
 3; 60 .
3; 60 .
10.2. Интегральные оценки качества переходных процессов
Интегральные оценки имеют целью дать общую оценку быстроты затухания и величины отклонения регулируемой величины в совокупности, без определения того и другого в отдельности. Они основаны на разработанных условных интегральных показателях, характеризующих отклонение реального переходного процесса системы от идеального. Под идеальным обычно понимают процесс, протекающий мгновенно без перерегулирования, или процесс, протекающий по экспоненте с заданными параметрами.
10.2.1. Линейная интегральная оценка. Пусть переходный процесс в системе автоматического управления вызывается единичным скачком задающего воздействия g(t) 1(t). Простейшей интегральной оценкой может служить величина
I1 ε(t)dt, |
(10.17) |
0 |
|
где ε(t) – отклонение регулируемой величины от нового установившегося значения, которое она будет иметь после завершения переходного процесса.
В устойчивой системе ε(t) 0 при t и этот интеграл имеет конечную величину. Геометрически это будет площадь под кривой переходного процесса, построенного для отклонения (рис. 10.5, а).
а |
б |
Рис. 10.5
221
Площадь будет тем меньше, чем быстрее затухает переходный процесс и чем меньше величина отклонения. Поэтому параметры системы рекомендуется выбирать таким образом, чтобы добиваться минимума этой интегральной оценки.
Для вычисления интеграла (10.17) нет необходимости в нахождении ε(t), так как его можно легко вычислить, используя изображение Лапласа. Действительно, изображение Лапласа определяется выражением
E(p) ε(t)e ptdt.
0
Отсюда следует, что интеграл (10.17) может быть найден посредством предельного перехода
ε(t)dt |
lim |
|
ε(t)e ptdt lim E(p). |
(10.18) |
0 |
p |
0 |
p 0 |
|
Неудобством интегральной оценки вида (10.17) является то, что она годится только для монотонных процессов, когда не меняется знак отклонения ε(t). Если же имеет место колебательный процесс (см. рис. 10.5, б), то при вычислении интеграла (10.17) площади будут складываться алгебраически и минимум этого интеграла может соответствовать колебаниям с малым затуханием или вообще без затухания. Так как форма переходного процесса при расчете систем регулирования может быть неизвестна, то применять интегральную оценку вида (10.17) оказывается практически нецелесообразным. Поэтому предлагалась другая интегральная оценка:
I2 |ε(t)|dt, |
(10.19) |
0 |
|
т. е. сумма абсолютных величин всех площадей по кривой переходного процесса. Но оказалось, что вычисление ее по коэффициентам уравнения затруднительно.
10.2.2. Квадратичная интегральная оценка. В свете вышесказанного целесообразно перейти к квадратичной интегральной оценке, называемой иногда «квадратичной площадью» регулирования:
222
|
|
I3 ε2(t)dt, |
(10.20) |
0 |
|
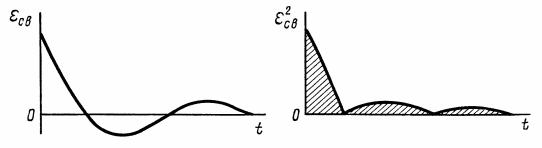
где ε(t) 0 при t . Эта оценка не зависит от знаков отклонений, а значит, и от формы переходного процесса – монотонной или колебательной (рис. 10.6, а).
Величина I (10.20) будет тем меньше, чем меньше сумма заштрихованных на рис. 10.6, б площадей (взятых для квадратов
ординат), т. е. чем |
лучше переходный процесс приближается |
к идеальному скачку |
регулируемой величины вслед за скачком |
задающего или возмущающего воздействия.
а |
б |
Рис. 10.6
Заметим, что оценку (10.20) называют также квадратичной динамической ошибкой регулирования.
При поступлении на вход системы единичного импульса g(t) δ(t) 1(t) получение реакции системы на единичный импульс (весовой функции) эквивалентно дифференцированию переходной функции, получающейся при действии единичного скачка.
В связи с этим квадратичную интегральную оценку при действии единичного импульса можно рассматривать в виде выражения
I4 |
w |
2 |
(t)dt |
|
2 |
dt, |
(10.21) |
|
[ε(t)] |
|
|||||
|
0 |
|
|
0 |
|
|
|
где w(t) – весовая функция системы по задающему или возмущающему воздействию, ε(t) – отклонение регулируемой величины от нового установившегося состояния в переходном процессе при действии единичной ступеньки задающего воздействия.
223

Интегральные оценки |
I3 и I4 (или выражения квадратичных |
|||
динамических |
ошибок) |
применяются |
для выбора |
структуры |
и параметров |
систем автоматического |
регулирования. |
При этом |
|
наилучшими параметрами считаются такие, при которых величина I3 или I4 имеет минимальное значение.
Рассмотрим методы вычисления квадратичных интегральных оценок.
Ошибка системы ε(t) hуст h(t), где h(t) – переходная функция. По определению
H(p) L[h(t)] 1 Ф(p) p
где L – оператор преобразования Лапласа. По теореме о предельных переходах
hуст limh(t) lim |
pH(p) |
|
t |
p 0 |
|
,
Ф(0),
следовательно,
E(p) L[ε(t)] Ф(0) 1 Ф(p). p
Поскольку Ф(p) – дробно-рациональная функция, то и записать в виде дробно-рациональной функции
E(p) b0 pm b1pm 1 ... bm 1p bm . a0 pn a1pn 1 ... an 1p an
E(p) можно
(10.22)
При |
m n |
оценку |
I3 |
|
(10.20) |
можно |
вычислить, используя |
||||||||||||
коэффициенты b0,b1, ,bm |
|
и a0, a1, , an (10.36), по формулам, |
|||||||||||||||||
приведенным ниже без вывода |
|
|
|
|
|
|
|
|
|
|
|||||||||
I |
|
|
|
ε2(t)dt |
1 |
B |
|
|
|
|
B |
|
|
... B |
B |
|
|
||
3 |
|
|
m |
|
0 |
||||||||||||||
|
|
|
|||||||||||||||||
|
|
|
|
2an2 |
m |
|
m 1 m 1 |
|
1 1 |
0 |
|
||||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bmbm 1 |
. |
|
|
|
|
|
(10.23) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
an2 |
|
|
|
|
I3 в функции |
||
Существуют |
таблицы |
для |
расчета |
интеграла |
|||||||||||||||
коэффициентов b0,b1, ,bm и a0, a1, , an для m n 1 и до n 10. Ниже приведены формулы для n 3:
224

n 1. I3 b02 /(2a0a1);
n 2. I3 (b12a0 b02a2)/(2a0a1a2);
n 3. I3 b22a0a1 (b12 2b0b2)a0a3 b02a2a3 .
2a0a3(a1a2 a0a3)
Вычисление квадратичных интегральных оценок I3 и I4 можно производить на основании так называемой формулы Релея, которая здесь будет приведена без доказательства.
Если E( jω) есть изображение Фурье функции времени ε(t), то существует зависимость, определяемая теоремой Парсеваля,
|
1 |
|
1 |
|
|
ε2(t)dt |
| E( jω)|2dω |
| E( jω)|2dω, |
|||
2π |
π |
||||
0 |
|
0 |
т. е. интегрирование квадрата функции по времени в пределах от нуля до бесконечности можно заменить интегрированием квадрата модуля изображения Фурье этой функции по всем частотам. При нахождении интегральной оценки I3, соответствующей реакции системы на входное задающее воздействие типа 1(t), изображение Фурье исследуемого отклонения ε(t) x( ) x(t) будет
E( jω) Ф(0) Ф( jω), j
где Ф( jω) – частотная передаточная функция замкнутой системы. Тогда
I3 |
1 |Ф(0) Ф( jω)|2 |
dω. |
|||
|
|
|
|||
π |
2 |
||||
|
0 |
|
|||
|
|
|
|
||
В астатических системах и статических системах с неединичной обратной связью или с масштабированием установившееся значение x( ) 1 и Ф(0) 1. Тогда (10.24) будет иметь вид
I3 |
|
1 |
|
|Фε( jω)| |
2 |
dω, |
(10.24) |
|
|
||||||
π |
2 |
|
|||||
|
|
0 |
|
|
|
где Фε( jω) 1 Ф( jω) – частотная передаточная функция замкнутой системы по ошибке.
Аналогичным образом для входного задающего воздействия типа единичного импульса δ(t), изображение которого равно 1, изображение Фурье исследуемого отклонения ε(t) x(t) равно
225

частотной |
передаточной |
функции |
замкнутой |
системы: |
|
E( jω) Фε( jω) 1. В результате получаем |
|
|
|||
|
|
1 |
|
|
|
|
I4 |
|Фε( jω)|2 dω. |
(10.25) |
||
|
π |
||||
|
|
0 |
|
|
|
|
|
|
|
|
|
Подобные выражения могут быть получены и для входного возмущающего воздействия, если вместо частотной передаточной функции Ф( jω) использовать передаточную функцию по возмущающему воздействию Фf ( jω).
10.2.3. Улучшенная квадратичная интегральная оценка.
Недостатком интегральных оценок является то, что здесь ничем не ограничивается форма кривой переходного процесса. Оказывается, например, что три совершенно различных по форме процесса, изображенных на рис. 10.7, имеют одно и то же значение квадратичной интегральной оценки I3 (10.20).
Рис. 10.7
Часто оказывается, что выбранные по минимуму этой оценки параметры системы соответствуют слишком сильно колебательному процессу, ибо отмечавшееся уже при этом стремление приблизить процесс к идеальному скачку вызывает большую скорость процесса при подходе к установившемуся значению ε( ) 0.
Это получается вследствие того, что оценка (10.20) учитывает только величину отклонения и быстроту затухания и никак не учитывает близость системы к колебательной границе устойчивости.
226
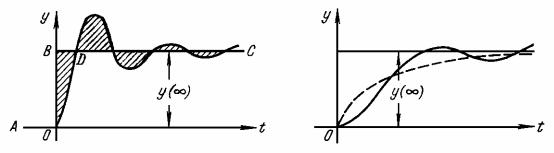
Если, например, подать на вход системы единичный скачок, то ошибка в переходном процессе определится заштрихованной частью на рис. 10.8, а. Очевидно, что величина интегральной оценки (10.20) будет тем меньше, чем ближе будет кривая переходного процесса к ломаной линии АОВС. Но приближение процесса к этой линии требует увеличения угла наклона кривой в начальной стадии процесса (приближение части кривой OD к отрезку ОВ).
а |
б |
Рис. 10.8
Увеличение же начальной скорости может вызвать значительное перерегулирование и, следовательно, малый запас устойчивости.
Поэтому применяется еще другой вид интегральной оценки, в которой ограничение накладывается не только на величину отклонения ε(t), но также и на скорость отклонения ε(t). Эта улучшенная квадратичная интегральная оценка имеет вид
|
2 |
|
2 |
2 |
(t)]dt, |
(10.26) |
|
I5 [ε |
(t) T |
||||||
|
ε |
|
|||||
0 |
|
|
|
|
|
|
где T – некоторая постоянная времени.
Выясним, какой вид переходного процесса будет получаться при выборе параметров системы регулирования по минимуму улучшенной интегральной оценки (10.26). Для этого проделаем следующие преобразования:
|
2 |
|
|
|
|
|
|
I5 [ε(t) Tε(t)] |
|
dt 2Tε(t)ε(t)dt |
|
0 |
|
|
0 |
|
|
|
|
[ε(t) Tε(t)]2dt Tε2(t)|ε00 |
[ε(t) Tε(t)]2dt Tε02, |
||
0 |
|
|
0 |
где ε0 – начальное значение отклонения в переходном процессе.
227
Наименьшее значение последнего выражения будет при выполнении условия
|
|
|
|
|
|
|
|
|
T (t) (t) (Tp 1)ε(t) 0. |
|
|||||||
Это есть дифференциальное уравнение первого порядка, |
||||||||
решение которого имеет вид |
|
|
|
|
||||
|
|
|
t |
|
|
t |
|
|
(t) |
|
|
|
(10.27) |
||||
0 |
e T ; |
x(t) x (1 e T ), |
||||||
|
|
|
|
0 |
|
|
|
|
где x0 ε0 – установившееся отклонение регулируемой величины. Этот процесс изображен на рис. 10.8, б пунктиром.
Следовательно, выбирая параметры системы по минимуму улучшенной интегральной оценки (10.26), можно приблизить переходный процесс к заданной экспоненте (10.27) с постоянной времени T, которая носит в этом случае название экстремали. Из этих соображений можно заранее задаться определенной величиной
T.
Выбор параметров системы по улучшенной квадратичной интегральной оценке приводит к менее колебательным процессам по сравнению с использованием обычной квадратичной интегральной оценки (10.20).
Методика вычисления интеграла (10.26) сводится к тому, что правая его часть разбивается на два слагаемых
I5 ε2(t)dt T2 ε2(t)dt.
0 0
При входном воздействии типа единичной ступенчатой функции первое слагаемое последнего выражения соответствует интегральной
оценке I3, а второе – T2I4. Поэтому в результате получаем для этого случая
I5 I3 T2I4.
Удобство интегральных оценок состоит в том, что они дают единый числовой критерий качества. Недостатком является то, что одному и тому же значению интегральной оценки могут отвечать разные формы переходного процесса, что создает недостаточную определенность решения задачи.
В принципе возможно использование более сложных выражений, чем (10.26), в которые кроме первой производной от отклонения будут входить вторая, третья и т. д. производные. Так,
228

например, ограничившись при подаче ступенчатого воздействия g(t)
отклонением |
ε(t), первой производной |
|
и второй производной |
|
ε(t) |
||||
|
|
|
|
|
ε(t), получим интегральную оценку в виде |
|
|
||
|
|
|
|
|
|
I6 [ε2(t) T12ε2(t) T24ε2(t)]dt. |
(10.28) |
||
|
0 |
|
|
|
Эта оценка будет характеризовать приближение переходного процесса к экстремали, определяемой решением дифференциального уравнения
T22 (t) T1 (t) ε(t) 0.
Экстремаль в данном случае будет соответствовать более сложной кривой, чем экспонента, что позволяет точнее задать желаемый вид переходного процесса.
Однако нахождение интегральных оценок вида
I6 I3 T12I3 T24I3,
к которым сводится вычисление интеграла (10.28), сопряжено со значительными трудностями, что ограничивает их применение.
Пример 10.2. Передаточная функция разомкнутой системы автоматического управления (см. рис. 9.1)
W(p) k . p
Определить оптимальное значение коэффициента передачи, соответствующее минимуму интегральной оценки
I [ε2(t) T2ε2(t)]dt.
0
Решение. Передаточная функция замкнутой системы по ошибке
Фε(p) |
kp |
|
|
p |
|
|
, гдеτ 1/k. |
|
|
||
p k |
τp 1 |
|
|
||||||||
|
|
|
|
|
|
|
|||||
Тогда изменение ошибки системы |
|
|
|
|
|
||||||
ε(t) Фε(p)1(t) e |
kt |
; |
|
|
kt |
. |
|
||||
|
|
ε(t) ke |
|
|
|
||||||
Интегральная оценка системы |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
1 |
|
|
I (e 2kt T2k2e 2kt)dt (1 T2k2) e 2ktdt |
|
(1 T2k2). |
|||||||||
|
|
||||||||||
0 |
|
|
|
|
|
|
0 |
|
2k |
||
|
|
|
|
|
|
|
|
|
|
||
229
Условие минимума интегральной оценки
|
dI |
2T2k 2k 2(1 T |
2k |
2) |
|
T2k2 1 |
0. |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4k2 |
|
|
|
2k2 |
|
||||
|
dk |
|
|
|
|
|
|
||||
Оптимальное |
значение |
|
|
коэффициента |
передачи, |
||||||
соответствующее минимуму I : |
|
|
|
|
|
|
|
|
|||
|
|
|
T2k2 1 0, |
тогда kопт T . |
|
|
|||||
10.3. Частотные методы оценки качества переходных процессов
Частотные методы исследования систем управления широко используют в инженерной практике. Они основаны на привычном для инженеров графическом изображении динамических характеристик системы, поэтому нашли широкое применение при расчетах систем автоматического управления и позволили разработать ряд удобных инженерных методов анализа и синтеза систем.
Большую роль в пропаганде и развитии частотных методов сыграли работы В. В. Солодовникова. В них приведены метод оценки качества по вещественным частотным характеристикам, метод построения переходных процессов по вещественным трапецеидальным характеристикам при ступенчатых воздействиях, а также метод синтеза корректирующих устройств. Применение этих методов позволяет определить такие важные показатели качества, как быстродействие, перерегулирование, колебательность процесса.
10.3.1. Определение переходного процесса по вещественной частотной характеристике. При воздействии на замкнутую систему с передаточной функцией Ф(p) единичной, ступенчатой функции g(t) 1(t) выходная величина является переходной характеристикой системы x(t) h(t). Переходная характеристика системы не удовлетворяет условию абсолютной интегрируемости и, следовательно, не может быть получена помощью обратного преобразования Фурье по частотным характеристикам замкнутой системы.
Поэтому определим сначала ее первую производную – импульсную переходную функцию w(t) h(t) L 1{Ф(p)}, которая удовлетворяет условию абсолютной интегрируемости, так как
230
