
Сборник задач
.pdf
Потерю напора на разветвленном участке L трубопровода мож- |
||||||||||||||
но подсчитать по формуле |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
L |
|
|
|
Q2 |
|
|
|||||
hп = 0, 0827λ |
|
|
Qт2 + |
|
п |
|
+ QпQт |
= |
||||||
d5 |
3 |
|||||||||||||
|
|
L |
|
q |
2L2 |
|
|
|||||||
|
= 0, 0827λ |
|
Qт2 + |
|
|
|
+ qLQт |
. |
(10.17) |
|||||
|
d5 |
|
3 |
|
|
|||||||||
4. Трубопроводы с кольцевыми участками |
|
|
||||||||||||
Кольцевой |
разветвленный |
уча- |
|
|
|
|
|
|
|
|||||
сток представляет собой в простей- |
|
|
|
|
|
|
|
|||||||
шем случае две параллельные трубы |
|
|
|
|
|
|
|
|||||||
между узлами |
A и В с одной или не- |
|
|
|
|
|
|
|
||||||
сколькими перемычками, соединяю- |
|
|
|
|
Рис. 10.13 |
|||||||||
щими промежуточные сечения этих |
|
|
|
|
||||||||||
труб (рис. 10.13). По перемычкам некоторое количество жидко- |
||||||||||||||
сти перетекает из одной трубы в другую. Направление потока в |
||||||||||||||
перемычке определяется величинами напоров в соединяемых пе- |
||||||||||||||
ремычкой сечениях. |
|
|
|
|
|
|
|
|
|
|||||
Жидкость может подаваться в кольцевой разветвленный уча- |
||||||||||||||
сток или отбираться из него через узлы |
А и В смыкания участка с |
|||||||||||||
подводящей и отводящей трубами или через узлы К |
и S на концах |
|||||||||||||
перемычек. При аналитическом расчете трубопровода с кольцевы- |
||||||||||||||
ми участками применяют метод последовательных приближений. |
||||||||||||||
Например, если при заданных размерах труб кольцевого участка |
||||||||||||||
известны величины притока и отбора жидкости в узлах и требуется |
||||||||||||||
определить расходы в трубах, |
то в качестве первого приближе- |
|||||||||||||
ния эти расходы задают удовлетворяющими условиям баланса расходов в узлахQ1Затемi выбирают первое замкнутое кольцо раз ветвленного участка. и для всех входящих в него труб вычисляют- потери напора Расходы считаются заданными правильно если ал гебраическая сумма. потерь напора в кольце равна нулю В, против- ном случае следует повторить выкладки при измененных. расходах- в трубах:
Q2i = Q1i ± Q1.
291
Поправка Q должна удовлетворять уравнению
|
|
|
|
|
λi |
Li |
Q2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Xi |
|
|
di5 |
1i |
|
|
|||||
|
Q1 = |
|
|
|
|
|
. |
|
|
||||||
|
|
2 Xi |
λi |
L1 |
|
|
|
|
|||||||
|
|
|
|
Q1i |
|
|
|||||||||
|
|
|
|
di5 |
|
|
|||||||||
Подбор расходов следует продолжать до тех пор, пока алгебра- |
|||||||||||||||
ическая сумма потерь напора в трубах рассматриваемого кольца не |
|||||||||||||||
станет равной нулю. |
Затем аналогичные вычисления повторяют по- |
||||||||||||||
следовательно для каждого из замкнутых контуров разветвленного |
|||||||||||||||
участка. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Расчет кольцевых трубопроводов с заданными размерами в |
|||||||||||||||
простых случаях можно проводить графическим способом. Рас- |
|||||||||||||||
смотрим такой способ применительно к схеме кольцевого участка |
|||||||||||||||
на рис. 10.13, предполагая, что жидкость подается в кольцо через |
|||||||||||||||
узел A и отбирается из кольца через узел В. |
|
|
|||||||||||||
При графическом решении задачи первоначально предполага- |
|||||||||||||||
ем, что перемычка KS перекрыта. В этом предположении Q1 = Q3 |
|||||||||||||||
и Q2 = Q4; кроме того, Q1 + Q2 |
= Q3 + Q4. |
|
|
||||||||||||
Для определения направления потока в перемычке составляют |
|||||||||||||||
уравнения характеристик труб 1 – 4: |
|
|
|
|
|
|
|
|
|
||||||
y |
y |
h |
|
|
y |
|
|
|
y |
|
|
h |
|
||
yA − yK |
= hп1; |
yA |
− yS |
= hп2;, ) |
(10.18) |
||||||||||
K − B |
= |
п3; |
S |
− B |
= |
|
п4 |
|
|||||||
где уA, уK, yS и уB – |
напоры в узлах; hп – |
потери напора в трубах, |
|||||||||||||
подсчитываемые по уравнению (10.1). |
|
|
|
|
|
||||||||||
Построения выполняем в следующем порядке. |
|
||||||||||||||
Если известен перепад напоров H = yA − yB и требуется опре- |
|||||||||||||||
делить расходы в трубах, выбираем вертикальную ось |
и пересе- |
||||||||||||||
каем ее горизонтальными осями |
х |
и |
х0, |
расстояние между которы- |
|||||||||||
ми Н . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
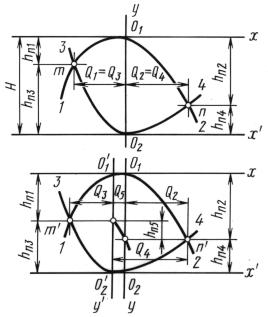
Точки пересечения обозначаем O1 и O2. |
из точек O1 |
и O2, как |
|||||||||||||
Строим кривые потерь в трубах 1, 2, 3 |
и 4 |
||||||||||||||
показано на рис. 10.14. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Абсцисса точки т пересечения кривых 1 и 3 дает при этом рас- |
|||||||||||||||
ход в ветви АKВ (Q1 = Q3), |
|
а абсцисса точки п пересечения кри- |
|||||||||||||
292 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
Рис. 10.14 |
|
= Q4) (см. рис. 10.13). Ор- |
||||||
вых 2 и 4 |
дает расход в ветви ASB (Q2 |
|||||||||||
динаты точек т и п (см. |
рис. 10.14), |
отсчитанные соответственно |
||||||||||
от осей х |
и х0, дают напоры, |
потерянные на участках 1, 2, 3 и |
4. |
|||||||||
По соотношению напоров, потерянных на участках 1 |
и 2, можно |
|||||||||||
установить направление потока в перемычке после ее открытия. |
В |
|||||||||||
случае, который показан на рис. 10.14, |
поток направлен от К |
к |
S |
|||||||||
(см. рис. 10.13). Расход |
Q5 и потеря напора hп5 в перемычке долж- |
|||||||||||
ны удовлетворять следующим уравнениям: |
|
|
|
|
||||||||
|
Q1 = Q3 + Q5; Q4 = Q2 + Q5; |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hп1 + hп5 = hп2; |
|
|
|
|
(10.19) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
hп5 + hп4 = hп3. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
При этом равенства |
|
1 + |
|
2 |
3 |
|
4 и п1 |
п3 = п2 + п4 |
||||
остаются в силе. |
Q Q = Q + Q h + h |
h h |
|
|||||||||
|
|
|
||||||||||
Для отыскания величин Q5 |
и hп5 на чертеж накладывается лист |
|||||||||||
кальки, на который наносятся оси |
x0 |
и y, а также кривые hп3 |
и |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
293 |
|
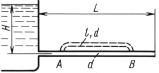
hп4. Калька передвигается влево, если hп1 < hп2, или вправо, если
hп1 > hп2. |
|
|
|
и n0 и |
|
Сдвинув кальку влево (см. рис. 10.14), отметим точки m0 |
|||||
проведем через них горизонтальные прямые. Эти прямые образу- |
|||||
ют с осями |
и y0 |
прямоугольник. На отдельном листе кальки по- |
|||
строим кривую hп5 = f (Qп5) для перемычки. Наложим эту кальку |
|||||
на чертеж так, чтобы начало кривой h 5 совпало с левым верхним |
|||||
углом прямоугольника. Кальки переместим до положения, |
при ко- |
||||
тором кривая hп5 |
пройдет через правый нижний угол прямоуголь- |
||||
ника. |
|
|
|
|
|
При этом расстояние между осями у и y0 показывает расход в пе- |
|||||
ремычке, а расстояние между горизонталями, проходящими через |
|||||
точки m0 |
и |
п, соответствует потере напора в перемычке. Абсциссы |
|||
точек m0 |
и n0, отсчитанные от оси y0, выражают расходы на участ- |
||||
ках, а ординаты, отсчитанные от осей х и х0, выражают потерянные |
|||||
на участках напоры. При этом уравнения (10.19) удовлетворяются. |
|||||
При отыскании напора Н , необходимого для пропуска через |
|||||
данную систему заданного расхода Q, кальку с кривыми |
3 |
и 4 и |
|||
осью у накладывают на чертеж с нанесенными кривыми 1 |
и |
2 так, |
|||
чтобы оси |
у и y0 |
совпали, а затем передвигают вверх или вниз, |
|||
пока сумма абсцисс точек пересечения кривых 1 и 3 и кривых 2 |
|||||
и 4 не будет изображать заданного расхода Q. После этого кальку |
|||||
с кривыми |
3 и 4 передвигают вправо или влево в зависимости от |
||||
получающегося направления потока в перемычке. |
|
|
|||
Накладывая кривую потерь в перемычке hп5 = f(Q5) на обра- |
|||||
зовавшийся на чертеже прямоугольник так, чтобы начало распола- |
|||||
галось в левом верхнем углу, перемещают кальки по вертикали до |
|||||
тех пор, пока hп5 не станет равной hп2 − h 1 или hп1 − h 2. |
|
||||
Рассмотренные выше методы расчета трубопроводов проиллю- |
|||||
стрируем некоторыми примерами. |
|
|
|||
|
|
|
Пример 1 (рис. 10.15). Для увели- |
||
|
|
|
чения при заданном напоре Н пропуск- |
||
|
|
|
ной способности трубопровода к нему |
||
|
|
|
между сечениями А и В присоединяют |
||
Рис. 10.15 |
параллельную ветвь. |
|
|
||
Определить, во сколько раз изме- |
|||||
нится расход в трубопроводе длиной диаметром если к нему присоединена параллельная ветвь тогоLже, диаметра dдлиной, l.
294
Считая трубопроводы длинными и предполагая наличие в них |
||||||||||||||||||||||||||||||||
турбулентных потоков, имеем для случая работы одного трубопро- |
||||||||||||||||||||||||||||||||
вода |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H = 0,0827λ1 |
|
Q12. |
|
|
|
|
|
|
|
|
(10.20) |
||||||||||||
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
||||||||||||||||
Для трубопровода с параллельнойdветвью |
|
|
|
|
||||||||||||||||||||||||||||
|
H = 0,0827λ2 |
L − l |
Q2 + 0,0827λ |
l |
|
Q22 |
. |
(10.21) |
||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
d5 |
2 |
|
|
|
|
|
|
d3 |
4 |
|
|
|
|||||||||
Сравнивая уравнения (10.20) и |
(10.21), получаем |
|||||||||||||||||||||||||||||||
|
|
|
|
λ1LQ12 = λ2(L − 1)Q22 + |
λlQ2 |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
, |
|
|||||||||||||||||||||
откуда |
|
4 |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q2 |
|
= v |
|
λ1L |
|
|
. |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
Q1 |
|
|
|
|
|
λl |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u |
λ2(L |
− |
1) + |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u |
|
4 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Поскольку при неизвестных расходах вычислить точные значе- |
||||||||||||||||||||||||||||||||
ния λ нельзя, задачу решим приближенно. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Принимая в первом приближении вели- |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
чины λ для всех труб одинаковыми, |
полу- |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
чаем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q2 |
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
= v |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Q1 |
|
|
3l |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
uL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
− 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В частном случае при L = l имеем |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
Q2 |
|
= 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Q1 |
|
|
|
|
|
|
как рас- |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
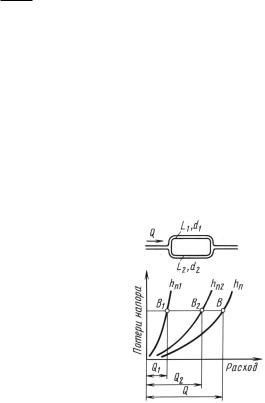
Пример 2 (рис. 10.16). Найти, |
|
|
|
|
|
|
|
|
Рис. 10.16 |
|||||||||||||||||||||||
пределится расход |
Q жидкости между дву- |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
мя параллельными трубами диаметрами d1 |
и d2, длинами (приве- |
|||||||||||||||||||||||||||||||
денными) L1 и L2 |
при значениях абсолютной шероховатости труб |
|||||||||||||||||||||||||||||||
1 и |
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Поскольку искомыми величинами в задаче являются расходы,
целесообразно избрать графический метод решения.
295
Построим характеристику первой трубы согласно уравнению
|
|
|
|
hп1 |
= 0,0827λ1 |
L1 |
Q2, |
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
d5 |
1 |
|
|
||
задавая ряд значений Q1 |
1 |
|
соответствующие вели- |
|||||||||
и вычисляя hп1; |
||||||||||||
чины λ1 определяются по заданной относительной шероховатости |
||||||||||||
|
d1 |
и значениям числа Рейнольдса (см. гл. 9): |
|
|
||||||||
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
4Q1 |
|
|
|
|||
|
|
|
|
|
Re1 = |
|
. |
|
|
|
||
|
|
|
|
|
πd1 ν |
|
|
|
||||
|
|
В тех же осях аналогично построим характеристику второй |
||||||||||
трубы |
|
|
|
|
L2 |
|
|
|
|
|||
|
|
|
|
hп2 |
= 0,0827λ2 |
Q2. |
|
|
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
d5 |
2 |
|
|
||
|
|
Складывая построенные кривые по2правилу суммирования ха- |
||||||||||
рактеристик параллельных труб, получим характеристику развет- |
||||||||||||
вленного участка. |
|
|
Далее на оси расходов находим |
|||||||||
|
|
|
|
|
точку, соответствующую суммарно- |
|||||||
|
|
|
|
|
му расходу Q, и проводим через нее |
|||||||
|
|
|
|
|
вертикаль до пересечения с харак- |
|||||||
|
|
|
|
|
теристикой |
разветвленного |
участ- |
|||||
|
|
|
|
|
ка. Через полученную точку |
В про- |
||||||
|
|
|
|
|
водим горизонталь до пересечения |
|||||||
|
|
|
|
|
с характеристиками первой |
(точка |
||||||
|
|
|
|
|
B1) и второй (точка B2) труб. |
Аб- |
||||||
|
|
|
|
|
сциссы полученных точек пересе- |
|||||||
|
|
Рис |
. 10.17 |
|
чения выражают искомые расходы |
|||||||
|
|
|
|
Q1 в первой и Q2 во второй трубах. |
||||||||
|
|
Пример 3 (рис. 10.17). Вода поступает из магистрали по трубам |
||||||||||
заданных размеров (l1 |
, d1 |
; l2, d2; l3, d3) и шероховатостей ( |
1, |
2, |
||||||||
|
3) в два резервуара, |
уровни в которых расположены на отметках |
||||||||||
A и B выше уровня оси магистральной трубы. |
|
|
||||||||||
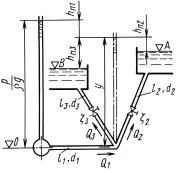
Определить при каком давлении р в магистрали в верхний ре зервуар будет поступать, расход Q2. -
296
По заданному расходу Q2 и шероховатости |
и |
2 трубы опреде- |
||||||||||||||||
ляем коэффициент сопротивления трения |
(λ2) |
эквивалентную |
||||||||||||||||
длину местных сопротивлений, установленных на второй трубе |
||||||||||||||||||
l2э = |
λ2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ζ2d2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Затем |
вычисляем напор у в узловой точке трубопровода: |
|
|
|||||||||||||||
|
|
|
y = A + 0,0827λ2L2 |
Q2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
2 |
, |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
d25 |
|
|
|
|
|
|||||
где L2 = l2 + l2э – приведенная длина второй трубы. |
|
|
||||||||||||||||
Расход Q3 определяем методом последовательных приближе- |
||||||||||||||||||
ний из уравнения Бернулли для третьей трубы: |
|
|
|
|
|
|||||||||||||
|
|
|
y − B = 0,0827λ3L3 |
Q2 |
|
|
|
|
|
|||||||||
|
|
|
3 |
, |
|
|
|
|
|
|||||||||
|
|
d5 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
. |
где L3 = l3 +l3э – приведенная длина третьей трубы l3э = |
λ3 |
|||||||||||||||||
Очевидно, |
|
|
|
|
|
|
|
|
|
|
|
ζ3d3 |
|
|||||
Q1 = Q2 + Q3. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Напор в магистрали |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
p |
= y + 0,0827λ1L1 |
Q2 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
1 |
, |
|
|
|
|
|
||||||
|
|
|
ρg |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
d15 |
|
|
|
|
|
|||||
где величина λ1 определяется по вычисленному расходу Q1 и за- |
||||||||||||||||||
данной шероховатости |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ЗАДАЧИ |
как распределяет- |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задача 10.1. Найти, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ся расход Q = 25 л/с между двумя парал- |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
лельными трубами, одна из которых име- |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ет длину l1 = 30 м и диаметр d1 = 50 мм, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
а другая (с задвижкой, |
коэффициент со- |
|
|
|
|
|
|
|
К задаче 10.1 |
|
|
|||||||
противления которой ζ = 3) |
имеет длину |
|
|
|
|
|
|
|
|
|
||||||||
l2 = 50 |
м и диаметр d2 = 100 |
мм. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Какова будет потеря напора hп в разветвленном участке? |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
297 |
|
Значения коэффициентов сопротивления трения труб принять |
|||
соответственно равными λ1 = 0,04 и λ2 = 0,03. Потери напора в |
|||
тройниках не учитывать. |
|
|
|
Ответ. Q1 = 4,45 л/с и Q2 = 20,55 л/с; hп = 6,3 м. |
|||
Задача 10.2. Смазочное масло (относительная плотность δ = |
|||
= 0,8, ν = 6 сСт) подводится к подшипникам коленчатого вала по |
|||
системе трубок, состоящей из пяти одинаковых участков, каждый |
|||
длиной l = 500 мм и диаметром d = 4 мм. |
|
||
1. Сколько смазки нужно подать к узлу А системы, чтобы ка- |
|||
ждый подшипник получил ее не менее |
8 см3 |
/с? |
|
2. Как изменится потребное количество смазки, если участки |
|||
АВ заменить трубой диаметром |
D = 8 |
мм? |
|
Давление на выходе из трубок в подшипники считать одинако- |
|||
вым, местными потерями и скоростными напорами пренебречь. |
|||
Ответ. 1. Q = 64 см3/с. 2. Q = 26 см3/с. |
|
||
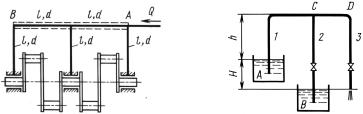
Задача 10.3. Сифонный трубопровод составлен из трех труб, |
|||
приведенные длины которых L1 |
= 50 |
м, L2 |
= 100 м, L3 = 150 м |
и диаметры d1 = 75 мм, d2 = 50 |
мм, d3 |
= 75 |
мм. |
Определить напор Н , необходимый для того, чтобы из резерву- |
|||
ара A в резервуар В поступала вода в количестве Q2 = 3 л/с. |
|||
Найти при этом напоре наименьшее давление pmin в трубопро- |
|||
воде, если h = 2 м и длина участка CD |
трубы 3 равна 20 м. |
||
Задачу решить в предположении квадратичной области сопро тивления труб приняв λ λ λ -
Скоростными, напорами1 =пренебречь0,025, 2 = 0,028, 3 = 0,025. Атмосферное давление принять равным. кПа
Ответ. Н = 11 м; рmin = 27,8 кПа. 100 .
К задаче 10.2 К задаче 10.3
Задача Резервуары и В с постоянными и одинаковыми уровнями воды10.4.соединены системойA труб, приведенные длины ко-
298
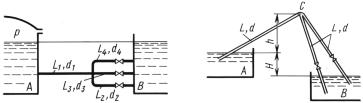
торых L1 = 400, L2 = 180, L3 |
= 50 и L4 = 400 м и диаметры |
d1 = d2 = d3 = 100 мм, d4 = 200 |
мм. |
При каком избыточном давлении р над поверхностью воды в резервуаре1. расход в трубе будет л с
КаковAпри этом суммарный4 расходQ4 = 40воды/ ? из резервуара в резервуар2. Q1 A
ЗадачуBрешить? в предположении квадратичной области сопро тивления приняв λ = λ = λ = 0,025 λ = 0,02 -
Ответ, . 1. р = 31,7 МПа2. 2. Q3 = 67,3 л/;с. 4 .
1 1
К задаче 10.4 |
К задаче 10.5 |
Ст), посту- |
|
Задача 10.5. |
Определить расход Q воды (ν = 0,01 |
||
пающей под напором Н = 5 м из резервуара A в резервуар В по |
|||
сифонному трубопроводу, состоящему из стальных ( |
= 0,2 мм) |
||
труб диаметрами d = 100 |
мм и приведенными длинами L = 100 м. |
||
Какова максимально возможная высота h расположения узла С |
|||
сифона, если предельно допустимая в этом узле вакуумметрическая |
|||
высота равна 10 |
м. |
|
|
Ответ. Q = 14,2 л/с; h = 6 м. |
|
||
Задача 10.6. |
Соляровое масло подается самотеком из резервуара |
||
A в резервуар В |
по трубопроводу, состоящему из трех одинаковых |
||
труб длинами L = 50 м и диаметрами d = 25 мм. |
|
||
1. Каким должен быть напор Н трубопровода, чтобы при темпе- |
|||
ратуре масла t = 10oС в резервуар В поступало масло в количестве |
|||
2. Как изменится расход при том же напоре, если температура |
|||
Q = 0,2 л/с? |
|
|
|
масла повысится до 20◦С? |
|
Местные потери напора в каждой трубе составляют 20 % от по- |
|
терь по длине. |
|
Зависимость кинематической вязкости масла от температуры |
|
задана графиком. |
л/с. |
Ответ. 1. H = 5,75 м. 2. Q = 0,3 |
|
|
299 |

|
|
|
|
|
К задаче 10.6 |
|
|
Задача 10.7. Два резервуара с постоянными и одинаковыми |
|||||
уровнями воды |
(ν = 0,01 Ст) соединены стальными (шерохова- |
|||||
тость |
= 0,2 |
мм) трубами, приведенные длины которых L1 |
= |
|||
= L3 |
= 50 |
м, L2 |
= 200 м и диаметры d = 100 мм. |
|
||
|
1. |
При каком напоре Н суммарный расход из баков Q = 12 л/с? |
||||
|
2. |
Какова максимально возможная высота h расположения узла |
||||
С при этом напоре. Предельную вакуумметрическую высоту в этом |
||||||
узле принять равной 10 м. |
|
|||||
|
Ответ. |
1. Н = 2,05 м. 2. h = 11,4 м. |
|
|||
|
Задача |
10.8. Определить магистральный расход воды в си- |
||||
стеме труб, |
соединяющих два резервуара с разностью уровней |
|||||
Н = 24 м, |
если размеры труб L1 = L2 = L3 = L4 = 100 |
м; |
||||
d1 |
= d2 = d4 = 100 мм; d3 = 200 мм. |
|
||||
|
Значения коэффициентов сопротивления трения в трубах λ1 |
= |
||||
= |
λ2 |
= λ4 |
= 0,025, λ3 = 0,02 и коэффициента сопротивления |
|||
задвижки ζ |
= 30. Потерями напора в остальных местных сопроти- |
|||||
влениях пренебречь. |
|
|||||
К задаче 10.7 |
К задаче 10.8 |
300
