2. Обработка данных опроса с помощью метода наименьших квадратов

Рассмотренная ранее функция спроса построена на использовании тех значений цены, которые были названы при опросе. Пока мы не знаем, какой будет спрос при других значениях цены. Может быть, и оптимальная цена будет находиться вне названных при опросе значений.

Поэтому целесообразно восстановить функцию спроса при всех возможных значениях цены, а затем использовать эту восстановленную зависимость для расчета оптимальной цены при различных значениях издержек.

Восстановить зависимость можно с помощью метода наименьших квадратов.

Метод наименьших квадратов относится к важному разделу организационно-экономического моделирования и прикладной статистики - многомерному статистическому анализу. В многомерном статистическом анализе исходные данные - это как минимум пара чисел (t_i, X_i) (а не одно число).

Предполагается, что переменная X линейно зависит от переменной t, т.е.

X(t) = a (t – t_ср.) + b

Это - теоретическая модель, а практически известны исходные данные – набор пар чисел (t_i, X_i), i = 1, 2, 3, …, n, где:

t_i – независимая переменная (например, время, а в случае определения выборочной функции спроса - цена p_i),

X_i – зависимая переменная (например, индекс инфляции, курс доллара, а в случае определения выборочной функции спроса это будет спрос D(p_i)).

Предполагается, что переменные связаны линейной зависимостью:

X_i = a(t_i – t_ср.) + b +e_i , i = 1, 2, 3, …, n.

Это - реальная зависимость, учитывающая погрешности (e_i), искажающие зависимость, параметры a и b нам неизвестны и подлежат оцениванию, а

t_ср. = .

Обычно параметры a и b оценивают методом наименьших квадратов.

Согласно этому методу для расчета наилучшей функции, приближающей линейным образом зависимость X от t, следует рассмотреть функцию двух переменных:

f(a,b) = -a(t_i – t_ср) – b]².

Фактически – это есть сумма квадратов разностей между реальными значениями функции и теоретически определенными значениями функции от независимой переменной.

Оценки метода наименьших квадратов – это такие значения a и b, при которых функция f(a,b) достигает минимума по всем значениям аргументов. Чтобы найти эти оценки, надо вычислить частные производные от функции f(a,b) по аргументам a и b, т.е. и, и приравнять их к 0.

Из полученных уравнений путем внутриматематических преобразований получим оценки:

_,

Следовательно, восстановленная функция, с помощью которой можно прогнозировать, имеет вид:

_.

Это - теоретическая функция, в которой вместо параметров подставлены их оценки, что позволяет проводить прогнозирование на какой-то интервал независимой переменной t вперед, а также интерполировать эти данные на моменты между наблюдениями.

Если взять другие обозначения, то линейная зависимость может выглядеть так:

i = 1, 2, 3, …. , n. (1)

Сравнивая выражения:

X_i = a(t_i – t_ср.) + b +e_i = at_i – at_ср. + b +e_i

и (1), легко перейти от одного к другому:

c =a, d = b – at_ср.

Аналогичные соотношения справедливы и для оценок:

c^* = a^*, d^* = b^* -a^*t_ср,

X_i^* = c^*t_i + d^*.

Оценкой погрешности (невязки) e_i является кажущаяся невязка

X_i - X_i^*.

Возникает вопрос, насколько точно оценивается зависимость. Чтобы ответить на него, надо ввести модель порождения данных:

,

где e_1, e₂……e_n - независимые, одинаково распределенные случайные величины с математическим ожиданием 0 и дисперсией .

Таким образом, модель описывается тремя параметрами: c, d и . Параметрыc и d мы умеем оценивать, а для оценки ² используется следующая формула:

=,

где SS - так называемая остаточная сумма квадратов, - оценка дисперсии.

Доверительные интервалы для прогностической функции записываются следующим образом (см. п.3.1 главы 3 настоящего учебника):

,

где ,

U() –квантиль стандартного нормального распределения порядка.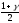

При доверительной вероятности = 0,95 находим из таблицU() = 1,96, при= 0,99 имеемU() = 2,58, иU() = 1,64 при= 0,9.

Теперь перейдем к обработке данных опроса с помощью метода наименьших квадратов. Для начала необходимо составить таблицу исходных данных – пар чисел (p, D(p)) также в порядке возрастания значений параметра p (см. табл. 3 на следующей странице). Далее рассчитаем прогностическую функцию и оптимальную цену при различных уровнях оптовой цены.

i	Цена pi	Ni	piNi	Спрос D(pi)	D(pi)Ni	(pi^2)Ni	D(pi)PiNi		D*(pi)	Ni[D(pi)-D*(pi)]
1	3000	5		50	250	45000000		750000	27,65
2	5000	4		45	180	100000000		900000	27.59
3	8000	7		41	287	448000000		2296000	27,49
4	10000	6		34	204	600000000		2040000	27,43
5	15000	3		28	84	675000000		1260000	27,27
6	20000	2		25	50	800000000		1000000	27.11
7	25000	1		23	23	625000000		575000	26,95
8	30000	4		22	88	3600000000		264000	26,79
9	34000	1		18	18	1156000000		612000	26,66
10	42000	1		17	17	1764000000		714000	26,41
11	50000	3		16	48	7500000000		2400000	26,15
12	80000	2		13	26	12800000000		2080000	25,19
13	90000	5		11	55	40500000000		4950000	24,87
14	100000	4		6	24	40000000000		2400000	24.55
15	150000	1		2	2	22500000000		300000	22,95
16	300000	1		1	1	90000000000		300000	18.15
Сумма		50	170300		1357	223113000000		22841000
Сумма/n	19240		3406		27,14

Таблица 3.

ценивание функции спроса методом наименьших квадратов.

участников опроса.

	Ni[D(pi)-D*(pi)]^2	pi^2
		9000000
		25000000
		64000000
		100000000
		225000000
		400000000
		625000000
		900000000
		1156000000
		1764000000
		2500000000
		6400000000
		8100000000
		10000000000
		22500000000
		900000000000
Сумма	2137,48	954768000000
Сумма/n	SS	19095360000

Теоретическая функция спроса:

D^*(p_i) = a(p - p_ср.) + b;

Перейдем к расчету восстановленной функции спроса:

D^*(p_i) = a*(p - p_ср.) + b*.

Необходимо найти оценки параметров a* и b*:

-0.000032

b* = 27,14; d* = b* - a*p_ср.= 27,14– (- 0,000032)*19240 = 27.75

Таким образом, восстановленная функция спроса имеет вид:

D*(p) = (-0,000032)p + 27.75

Из табл.2 видно, что остаточная сумма квадратов SS = 2137,48. Исходя из этого, найдем оценку среднего квадратического отклонения:

== 6,53.

Затем найдем доверительные границы для функции спроса:

D^*(p)_{верхн.\нижн.} = a^* p + d^*1,96

D^*(p)_{верхн.\нижн.} = (-0,009)p + 62,11,96=

= (-0,009)p_i +62,1.

Из табл.3 видно, что остаточная сумма квадратов SS = 2795,81. Исходя из этого, найдем оценку среднего квадратического отклонения:

Затем найдем доверительные границы для функции спроса:

Например, при p = 8000

D^*(8000) _верхн. = 34,32 + 2,31 = 36,63,

D^*(8000)_нижн. = 34,32 – 2,31 = 32,01.

Таким образом, при цене 8000 руб. товар купят 33-37 человек.

Рис.2. Выборочная и восстановленная функции спроса

Теперь перейдем к расчету оптимальной цены при различных уровнях издержек p₀. Для этого мы должны максимизировать прибыль:

(p - p_0.) D^*(p) = (p_. – p_0.)(a*p + d*).

Продифференцируем это выражение по p и приравняем 0 производную:

,

2a*p_опт. – а*р₀ +d* = 0,

p_опт. = .

Поскольку a* = -0,0012, a d* = 43,92 ,то

Как видно из последней формулы, при возрастании издержек оптимальная розничная цена также возрастает, но вдвое медленнее.

Сравним (табл.4) оптимальные цены, найденные с помощью метода наименьших квадратов (p_опт.2) и рассчитанные ранее с помощью первого метода (p_опт.1).

Таблица 4.

Сравнение методов расчета оптимальной цены.

p0	pопт.2	pопт.1
2000	19148,76	15000
5000	20648,76	15000
8000	22148,76	15000
13000	24648,76	40000
21000	28648,76	50000

Проанализируем результаты, представленные в табл. 3 и 4.

Согласно табл.3, при расчете восстановленной функции D*(p) при p = 40000 получаем отрицательную величину (-4,38), что не имеет смысла, т.к. спрос не может быть отрицательным. Рассмотри ситуацию подробнее. Функция спроса убывает, коэффициент a* отрицателен, поэтому рано или поздно прямая уйдет в отрицательную область. Это значит, что приближение функции спроса линейной зависимостью может быть корректно лишь на некотором отрезке, а не на всей прямой. Выясним, при какой цене спрос достигает 0:

D*(p) = (-0,0012)p +43,92 = 0,

Т.е. корректное приближение функции спроса линейной зависимостью может быть при цене p меньшей, чем 36600 рублей.

Общепринятых простых методов, позволяющих избежать отрицательных оценок функции спроса, нет. Если получаем отрицательные величины, то должны указать область, в которой линейная зависимость дает корректную оценку, что и сделали выше, когда D*(p) приравняли к 0.

Рассмотрим теперь табл.4. Здесь видим разницу между расчетной оптимальной ценой p_опт.2, полученной с помощью метода наименьших квадратов, и расчетной ценой p_опт.1, найденной исходя только из данных опроса. Это связано с тем, что потребитель всегда склонен к круглым числам (например, большинство назовет 19000 руб., а не 19148 руб. 76 коп.). Мы же при применении метода наименьших квадратов ищем максимум не только среди названных опрощенными значений, а по более обширному множеству.