
студ ивт 22 материалы к курсу физики / kingsep_as_lokshin_gr_olkhov_oa_kurs_obshchei_fiziki_osnovy
.pdf
7.6 ] |
Связь функции когерентности и распределения энергии |
551 |
пустимую (для наблюдения интерференционной картины) разность хода можно оценить из условия: 2 $, здесь — значение , при котором функция «огибающей» (выражение в квадратных скобках) обращается в нуль:
27 |
(7.39) |
|
Максимальный порядок интерференции есть |
|
|
|
27 |
(7.40) |
0 |
0 |
|
Сопоставляя выражения для максимально допустимой разности хода, полученные при временном ( >0) и спектральном (формула (7.39)) подходах, находим связь между шириной спектра и временем корреляции >0
>0 2$ |
(7.41) |
Сужение спектра приводит, согласно (7.41), к увеличению времени когерентности >0, т. е. к увеличению длительности цу-
гов; наоборот, чем короче цуги, тем шире спектр — таков смысл соотношения (7.41), называемого соотношением неопределенностей.
Выражая ширину спектрального интервала в длинах волн, имеем для и следующие соотношения:
|
0 |
; |
2 |
|
(7.42) |
||
|
|
0 |
|
||||
|
|
|
|||||
|
|
|
|
|
|
||
Приведем числовые |
оценки |
и |
для некоторых |
||||
реальных источников. |
|
|
|
1. |
Дуговой фонарь без фильтра, визуальное наблюдение |
||
|
2,5–3 10 5 см, |
0 5 10 5 см; |
|
|
2; 10 4 см |
||
2. |
То же со стеклянным светофильтром |
||
|
Æ |
|
0 5 10 5 см; |
|
300 А 3 10 6 см, |
|
|
|
20, 10 3 см |
||
3. |
Узкая спектральная линия |
|
|
|
Æ |
|
2,5 м |
|
10 3 А, 5 106; |
||
4. Излучение стабилизированного газового лазера
1010; 5 км
Соотношение неопределенностей (7.41) получилось не случайно. Оно является следствием общей связи, существующей
552 |
Интерференция волн |
[ Гл. 7 |
между функцией когерентности > и спектральной интенсивностью . К нахождению этой связи мы и перейдем.
Вернемся к соотношению (7.37), представив правую часть равенства в виде
: 2 2
7
Интеграл в первом слагаемом представляет собой суммарную интенсивность света в каждой из интерферирующих волн:
:0,
(т. е. первое слагаемое 2:0 — это сумма интенсивностей слагаемых волн). Второе слагаемое перепишем в виде
2 2 Re D # %
7
Таким образом, вместо (7.37) имеем
: 2:0 1 |
Re < # |
|
|
||
+0 |
|
|
Сравнивая полученное выражение с (7.33), найдем
D # % :05 > >
Итак, функция — распределение энергии по спектру — является преобразованием Фурье функции когерентности >
> D # |
(7.43) |
Понятно, что соотношение неопределенностей (7.41), связывающее ширину спектра со временем когерентности, являет-
ся следствием общей связи (7.43).
Замечание. Качественно ясно, почему с ростом ширины спектра излучения контраст интерференционных полос уменьшается. Это связано с тем, что полосы, отвечающие разным частотам (разным длинам волн), имеют разную ширину ( *). Полосы, отвечающие б´ольшим длинам волн, более широкие, поэтому с ростом порядка полосы (т. е. с ростом разности хода) смещение полос одинакового порядка , отвечающее разным , постепенно нарастает. Наконец, наступает ситуация, когда на 1 -ю полосу длины волны налагается -я полоса длины волны , т. е.
1

7.7 ] Пространственная когерентность и интерференционные явления 553
При дальнейшем росте полосы практически исчезают: на минимум интенсивности одной длины волны налагается максимум какой-либо другой длины волны из спектрального диапазона излучения. Суммарная картина интенсивности усредняется. Из последнего равенства получаем уже знакомую нам оценку максимального порядка интерференции .
7.7. Пространственная когерентность и интерференционные явления при использовании протяженных источников
До сих пор речь шла о том, как на интерференционных явлениях сказывается отличие реальной волны от строго монохроматической. При этом источники света считались точечными (содержащими однако огромное число излучающих атомов).
Понятие «точечный источник» — идеализация, ничуть не меньшая, чем понятие «монохроматический источник». Все источники света имеют определенную протяженность, а это приводит к возникновению интерференционной картины меньшей контрастности, чем это следует из приведенных ранее расчетов. Как показывает опыт, при увеличении размеров источника видность интерференционной картины постепенно уменьшается и при достаточно больших размерах интерференционные полосы исчезают вовсе. Легко качественно понять характер изменения видности полос при изменении размеров источника, если исхо-
дить из представления о том, что протяженный источник света — это совокупность большого количества независимых источников
(рис. 7.18) (действительно, каждая малая |
Vi |
|||
площадка источника 9 состоит |
из ато- Si |
|||
мов, излучающих независимо от атомов |
|
|||
другой площадки, 9 ( |
")), |
и таким |
Vj |
|
образом волны, излучаемые этими площад- |
||||
|
||||
ками, 2 и 2 некогерентны: |
|
S j |
||
|
|
|
||
2 2 0 при |
" |
|
Рис. 7.18 |
|
Некогерентность излучения разных точек (малых элементов9) протяженного источника означает, что при расчете интерференционой картины необходимо найти распределение интенсивности, создаваемое каждой точкой, а затем сложить интенсивности.
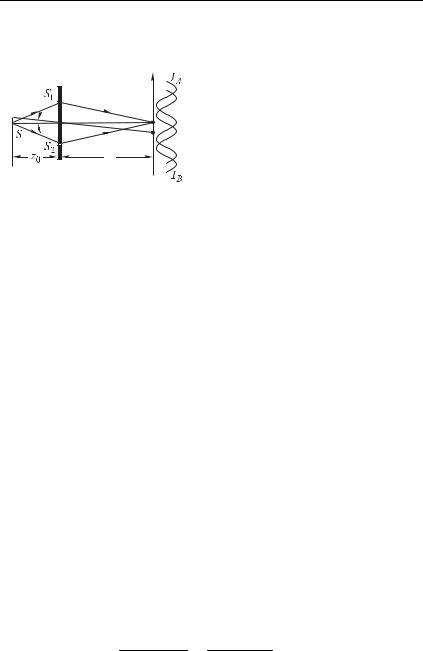
Пусть источник 9 и плоскость наблюдения в опыте английского физика Т. Юнга (1773–1829) удалены от экрана с отверстиями 91 и 92 настолько, что волны, приходящие от каждого малого элемента источника к этим отверстиям, а также волны, приходящие к плоскости наблюдения от этих отверстий,
554 |
Интерференция волн |
|
[ Гл. 7 |
||||
можно считать плоскими. Тогда, очевидно, интерференционная |
|||||||
картина, создаваемая крайней точкой источника (штриховая |
|||||||
кривая : на рис. 7.19), смещена относительно интерференци- |
|||||||
|
x |
онной картины |
от центральной |
||||
|
точки (сплошная кривая : ) |
||||||
|
|
на расстояние, равное #. Если |
|||||
B |
|
это смещение меньше ширины ин- |
|||||
A |
|
терференционной полосы * |
|||||
|
|
(* |
— угол схождения ин- |
||||
z |
|
терферирующих |
волн, |
— |
рас- |
||
|
|
стояние |
между |
отверстиями |
91 |
||
Рис. 7.19 |
|
и 92), то интерференционная кар- |
|||||
|
тина наблюдается. |
|
|
||||
|
|
|
|
||||
В противном случае (при # & ) интерференция не наблю- |
|||||||
дается: суммарная интенсивность уже не имеет чередующихся |
|||||||
максимумов и минимумов. Это связано с тем, что на темную |
|||||||
полосу (минимум интенсивности от одной точки источника) на- |
|||||||
кладывается светлая полоса (максимум интенсивности от другой |
|||||||
точки), и суммарная интенсивность оказывается константой — |
|||||||
получается равномерная освещенность плоскости наблюдения. |
|||||||
Итак, имеем оценку для максимально допустимой ширины ис- |
|||||||
точника : |
|
0 , |
|
|
(7.44) |
||
|
|
|
|
||||
или при заданной ширине источника, максимально допустимое |
|||||||
расстояние между отверстиями |
(которое определяет «апертуру |
||||||
интерференции» |
0) |
|
|
|
|
|
|
|
0 |
или |
|
(7.45) |
|||
|
) |
|
|
) |
|
|
|
Мы привели лишь качественные рассуждения, которые не |
|||||||
дают количественной оценки видности интерференционной кар- |
|||||||
тины. Такая количественная оценка тесно связана с важным |
|||||||
свойством волны, излучаемой протяженным источником света, |
|||||||
с пространственной когерентностью. |
|
|
|
|
|||
Если в опыте Юнга используется точечный источник света 9, |
|||||||
находящийся на одинаковом расстоянии от отверстий 91 и 92, |
|||||||
то волны от этого источника создают на отверстиях одинаковые |
|||||||
колебания: амплитуда и фаза колебаний 21 в точке 91 в любой |
|||||||
момент времени такие же, как и в колебании 22 (в точке 92): |
|||||||
21 22 2
Отметим, что при этом
21 22 2 2 :
Таким образом, колебания 21 и 22 полностью когерентны.
7.7] Пространственная когерентность и интерференционные явления 555
Вслучае протяженного источника колебания в точках 91 и 92 создаются всеми точками источника, причем лишь центральная точка источника создает на отверстиях одинаковые по амплитуде и фазе колебания. Любая другая точка посылает волну, создающую на отверстиях разные по фазе колебания (просто из-за того, что она находится на разных расстояниях
от 91 и 92). Ясно поэтому, что и суммарное колебание 21 в точке 91 отличается по фазе от колебания 22 в точке 92. Это приводит, как мы увидим, к уменьшению величины
|
12 0 21 22 |
|
|
|
|
|||
Как мы вскоре убедимся, 12 0 является функцией расстояния |
||||||||
между точками |
91 и 92 |
. Она называется функцией простран- |
||||||
ственной когерентности. |
|
|
|
|
|
|
||
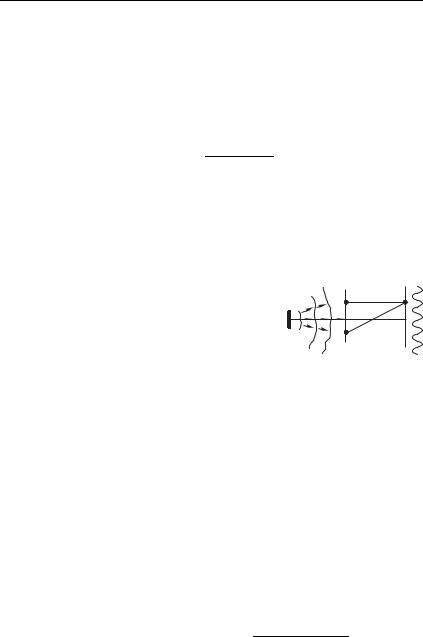
Пусть 21 и 22 — колебания, созданные протяжен- |
||||||||
ным квазимонохроматическим источником 9 в точках 91 и 92 |
||||||||
плоскости П1 (рис. 7.20). Чтобы экспериментально определить, |
||||||||
когерентны ли колебания 21 и 22 |
|
|
|
|
|
|||
установим в плоскости |
П1 |
непрозрач- |
|
|
S1 |
r1 |
P |
|
ный экран, проделав два малых отвер- |
|
|
|
|
||||
|
|
|
|
|
||||
стия в точках 91 и 92. |
|
|
S |
|
|
r2 |
|
|
|
|
|
|
|
|
|||
Волны света, проходя через отвер- |
|
|
S2 |
|
||||
|
|
|
|
|||||
стия, идут (из-за дифракции) в разных |
|
|
Ï1 |
Ï2 |
||||
направлениях и, перекрываясь, создают |
|
|
Рис. 7.20 |
|
||||
(или не создают) интерференционную |
|
|
|
|||||
|
|
|
|
|
||||
картину в плоскости наблюдения П2. Эта картина, как мы уви- |
||||||||
дим, даст нам информацию о функции когерентности 21 22 . |
||||||||
Колебание в точке наблюдения 6 есть результат наложения |
||||||||
волн, пришедших в эту точку от 91 и 92. |
|
|
|
|
||||
Колебания, созданные волной, пришедшей от отверстия 91, |
||||||||
запишем в виде #121 >1 , где константа #1 учитывает ослаб- |
||||||||
ление волны из-за расходимости, а >1 1 |
есть время рас- |
|||||||
пространения волны от |
91 |
до 6, т. е. колебание |
в точке 6 |
|||||
в момент такое же, как на отверстии 91 в момент >1, лишь |
||||||||
уменьшенной амплитуды. |
|
|
|
|
|
|
||
Аналогично |
волна |
от |
отверстия |
92 |
создает |
колебание |
||
#222 >2 , где >2 2 . Результирующее колебание, согласно |
||||||||
принципу суперпозиции, есть |
|
|
|
|
|
|||
2 #121 >1 #222 >2
Как и ранее, находим
: 2 2 :1 :2 2 Re 21 22 >
Будем считать, что для всей интересующей нас области наблюдения запаздывание одной волны относительно другой > ма-

556 |
Интерференция волн |
[ Гл. 7 |
ло по сравнению со временем когерентности >0 (но конечно, может быть много больше периода светового колебания 2$ 0), > >0.
Это означает, что за время > ( 1 2) амплитуда и фаза колебания 22 не успевает заметно измениться, т. е. колебание в момент времени > состоит из той же совокупности цугов, что и в момент времени .
Тогда
72 > 72 и 22 > 72 > D# 72 D#
Вспомнив определение функции пространственной когерент-
ности, получаем |
|
: :1 :2 2 Re 12 0 D#0 |
(7.46) |
Из (7.46) следует, что интенсивность света во всех максимумах интерференционной картины одна и та же (независимо от порядка интерференции), так как величина 12 0 не зависит от положения точки наблюдения (не зависит от > при условии что > >0), а определяется лишь апертурой интерференции (в опыте Юнга — угловым расстоянием между отверстиями 91 и 92) или, при заданном расстоянии, размерами источника. Таким образом, видность интерференционной картины одинакова во всех точках.
Вводя, как и ранее, нормированную функцию
512 0 12 0 ,
+1+2
называемую степенью пространственной когерентности, получим из (7.46)
: > :1 :2 2 :1:2 Re 512 0 D#0 |
(7.47) |
Или, при равных интенсивностях :1 :2 :0 |
|
: > 2:0 1 Re 512 0 D#0 |
(7.48) |
Полученные выражения (7.47) и (7.48), определяющие интерференционную картину при использовании протяженного источника, справедливы для любой двухлучевой интерференционной схемы. Формулу (7.48) можно записать в виде
: > 2:0 1 512 0 0> , |
(7.49) |
где — аргумент комплексной функции 512. Видность 2 выражается через 512 0 равенством
2 512 0
Пока мы имеем лишь качественную оценку (7.45) влияния размеров источника на видность интерференционной картины. Теперь необходимо найти количественную связь функции 512 0 с размером источника.
7.7 ] Пространственная когерентность и интерференционные явления 557 |
||||||
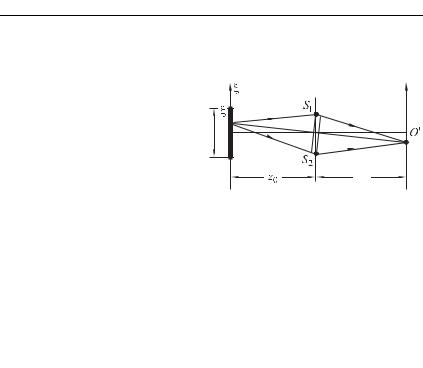
Для этого рассмотрим интерференционную картину, создава- |
||||||
емую протяженным источником, как сумму интерференционных |
||||||
картин от отдельных точек источника. В качестве примера вновь |
||||||
обратимся к |
опыту |
Юнга |
|
|
x |
|
(рис. 7.21). |
|
|
|
|
|
|
|
|
|
|
|
|
|
Протяженный |
источ- |
|
|
|
||
ник — светящаяся полоска |
b O |
|
|
|||
шириной — и плоскость |
|
x |
||||
|
|
|||||
наблюдения |
П |
находятся |
|
|
|
|
на расстояниях 0 и от |
|
z |
|
|||
экрана с отверстиями 91 |
|
|
Ï |
|||
и 92, расстояние между |
|
Рис. 7.21 |
|
|||
отверстиями . |
|
|
|
|
|
|
Еще раз подчеркнем, что степень монохроматичности ис- |
||||||
точника достаточно велика (т. е. для всей интересующей нас |
||||||
области наблюдения в плоскости П разность хода волн много |
||||||
меньше длины |
цуга |
>0). Поэтому |
можно при |
расчете |
||
картины интерференции, созданной какой-либо точкой источни- |
||||||
ка, пользоваться приближением строго монохроматических волн |
||||||
(формула (7.8)) заданной частоты. |
|
|
||||
Картина интерференции, созданная в плоскости наблюдения |
||||||
центральной точкой источника « » (точнее малым элементом |
||||||
источника) имеет вид |
|
|
|
|||
|
0 2 0 1 |
2 |
|
|
|
||
Здесь 0 |
— интенсивность волны, прошедшей через од- |
||
но из отверстий (и созданной в плоскости наблюдения малым элементом источника ), — ширина интерференционной полосы. Ясно, что нулевая полоса (соответствующая разности хода 0) находится на оси симметрии, в точке .
Из рис. 7.21 также ясно, что элемент источника, имеющий координату 0, создает картину интерференции, смещенную на расстояние 0 0 (в точку смещается нулевая полоса, соответствующая разности хода 0). Мы полагаем, что расстояния 0 и велики по сравнению с размером источника и
расстоянием между отверстиями |
|
, т. е. |
|
|
|
|
|
|
|
||||
2 0 |
1 |
2 |
|
|
|
|
|
0 |
|
(7.50) |
|||
|
|
|
|||||||||||
|
|
|
|
|
0 |
|
|||||||
Результирующую картину интерференции найдем суммирова- |
|||||||||||||
нием картин (7.50) по всем точкам источника. Получаем |
|
||||||||||||
/2 |
|
2 |
|
|
|
|
|
|
|
||||
: 2 0 |
1 |
|
|
|
|
|
(7.51) |
||||||
|
|
|
|
|
|
0 |
|
||||||
|
|
|
|
0 |
|||||||||
/2
558 Интерференция волн [ Гл. 7
Производя интегрирование (7.51), найдем
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
#" |
|
|||||
: 2:0 !1 |
|
0) |
|
(7.52) |
||||||||
|
|
|
|
|
|
|
|
|
$ |
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0) |
|
|
|
|
|
|
|||
Сравнивая (7.52) и (7.49), находим степень пространственной когерентности, которая определяет видность интерференционной
картины:
|
|
|
2 512 |
|
|
0) |
|
(7.53) |
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
0) |
|
|
||
|
|
|
|
|
|
|
|
|
|
||
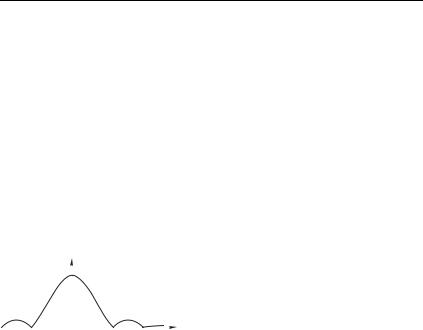
Функция 512 изображена на рис. 7.22 (аргументом является |
|||||||||||
расстояние |
между точками 91 и 92). Как следует из (7.53), |
||||||||||
|
|
|
|
|
степень когерентности |
колебаний |
|||||
|
|
12 |
|
|
в двух точках, разнесенных на |
||||||
|
|
|
|
|
расстояние |
уменьшается от 1 |
|||||
|
|
|
|
|
при |
|
0 до нуля при |
30 |
|||
|
|
|
d |
2$ . |
|
||||||
|
|
|
|
|
|
Таким образом, если расстоя- |
|||||
0 |
|
|
0 |
|
|
||||||
|
|
|
ние между точками 91 и 92 мень- |
||||||||
|
|
|
|
|
|||||||
Рис. 7.22 |
ше , то колебания в этих точ- |
||||||||||
ках частично когерентны: при этом |
|||||||||||
|
|
|
|
|
|||||||
512 0. При |
512 0, т. е. колебания в точках 91 и |
||||||||||
92 некогерентны.
Величину 30 называют радиусом пространственной когерентности, а площадку с линейным размером называют площадкой когерентности. Вводя угловой размер источника
B 0, можно записать
30 |
|
|
(7.54) |
|
F |
|
|
Итак, колебания в любых двух точках, лежащих внутри площадки размером 30 частично когерентны, а в точках, расстояние между которыми больше 30 — некогерентны.
Возвращаясь к опыту Юнга, можно иначе, чем это сделано выше, сформулировать условия, при которых можно наблюдать интерференционную картину. Если расстояние между отверстиями 91 и 92 меньше радиуса когерентности, то интерференция наблюдается. Аналогичное условие можно сформулировать для любой интерференционной схемы: апертура интерференции должна быть меньше углового размера площадки когерентности.
Если зафиксировать расстояние между точками 91 и 92 и приближать плоскость , в которой они находятся, к источнику, то, как следует из (7.53), степень когерентности колебаний
7.8 ] |
Интерферометры и интерферометрия |
559 |
в этих точках уменьшается. При стремлении 0 к нулю (плоскость придвинута вплотную к источнику) колебания в любых двух точках, как угодно близко расположенных, некогерентны (ведь любые две точки источника излучают некогерентно). Наоборот, с удалением плоскости колебания в точках 91 и 92 становятся все более когерентными и при достаточном удалении когерентность колебаний становится полной. Размер площадок когерентности по мере удаления от источника постепенно (пропорционально ) увеличивается. Мы видим, таким образом, что первоначально некогерентное поле излучения в процессе распространения приобретает частичную когерентность. В этом и состоит смысл соотношения (7.53).
7.8. Интерферометры и интерферометрия
Явление интерференции находит широкое применение при решении самых разнообразных физических и технических про-
блем. Используемые для этого оптические устройства называются интерферометрами (например, интерферометры Майкельсо-
на на рис. 7.13), а область оптики, исследующую возможности использования интерферометров называют интерферометрией.
Мы убедились ранее, что интерференционная картина позволяет получить информацию о временн´ой степени когерентности 5 > , а следовательно и о спектральном составе излучения . Это, в свою очередь, дает информацию о физических процессах в источнике (энергетических уровнях атомов, процессах их взаимодействия, температуре и т. д.).
С другой стороны, измерения видности интерференционной картины, созданной каким-либо протяженным источником, дают возможность определить его угловой размер. Интерференционный метод определения угловых размеров звездных объектов (либо измерения углового расстояния между компонентами двойных звезд) был предложен и реализован американским физиком А. Майкельсоном (1852–1931).
Видность интерференционной картины в фокальной плоскости объектива « » в схеме звездного интерферометра Майкельсона (рис. 7.13 е) зависит от степени когерентности колебаний на зеркалах 1 и 2 (эти колебания созданы излучением какой-либо удаленной звезды — протяженного источника света).
Расстояние E между зеркалами 1 и 2 называется базой интерферометра и может изменяться. Пока это расстояние
мало (меньше радиуса когерентности) степень когерентности колебаний в точках 1 и 2 достаточно велика и интерференционная картина в фокальной плоскости Э объектива достаточно четкая. По мере увеличения E видность картины постепенно

560 |
|
|
|
|
Интерференция волн |
[ Гл. 7 |
||
уменьшается и при E 30 (30 — радиус когерентности, опреде- |
||||||||
ляемый формулой (7.54)) интерференционная картина полностью |
||||||||
исчезает. Определяемый угловой размер звезды равен |
|
|
||||||
|
|
|
|
|
B |
(7.55) |
||
|
|
|
|
|
%0 |
= |
|
|
|
Таким образом Майкельсону удалось определить угловой |
|||||||
размер красного гиганта в созвездии Ориона — звезды Бе- |
||||||||
тельгейзе. Измеренный экспериментально радиус когерентности |
||||||||
оказался равным 6 м, а значение B, рассчитанное по формуле |
||||||||
(7.55), равным 0,0047 . Для сравнения, угловой размер Солнца |
||||||||
B 30 10 2 |
рад, а соответствующий радиус когерентности |
|||||||
30 0,06 мм. |
|
|
|
|
, |
|||
|
Вообще подавляющее большинство звезд имеет диаметр |
|||||||
мало отличающийся от диаметра Солнца, поэтому их угловой |
||||||||
размер B |
|
(в силу огромности расстояния ) чрезвычайно |
||||||
мал. Поэтому для измерений угловых размеров большинства |
||||||||
звезд требуются интерферометры с базой E в несколько де- |
||||||||
сятков метров. Создание оптических устройств с такой базой |
||||||||
чрезвычайно сложная техническая проблема: ведь нужно обес- |
||||||||
печить высокую стабильность расположения зеркал 1 и 2 |
||||||||
в процессе измерения («дрожания» одного зеркала относительно |
||||||||
другого порядка длины световой волны ( 5 10 7 м) приводят |
||||||||
к полному исчезновению картины интерференции). Серьезной |
||||||||
помехой является также атмосферная турбулентность. |
|
|
||||||
|
Проблему позволяют решить радиоинтерферометры. Роль |
|||||||
зеркал 1 и 2 играют в данном случае радиотелескопы (две |
||||||||
радиоантенны), принимающие сигнал с измеряемого источника |
||||||||
в диапазоне радиоволн ( 10 см). Эти две антенны могут рас- |
||||||||
полагаться даже на разных континентах, так что база интерфе- |
||||||||
рометра E может быть тысячи и десятки тысяч километров. Сиг- |
||||||||
налы с двух радиотелескопов подают на общий детектор, изме- |
||||||||
ряющий интенсивность суммарного сигнала. При использовании |
||||||||
радиоинтерферометров переход от коротких (оптических) длин |
||||||||
волн к длинным (радиоволнам) компенсируется увеличением ба- |
||||||||
зы интерферометра, поэтому угловой размер измеряемого объек- |
||||||||
|
|
|
|
|
та B E может быть чрезвычайно |
|||
|
|
|
|
|
малым (примерно в 100 раз меньше, |
|||
|
S1 |
Ê |
|
чем при использовании «оптического» |
||||
|
|
|
1 |
|
интерферометра Майкельсона). |
|
|
|
S |
S |
|
Ê2 |
|
|
|
||
2 |
|
Широкое применение находят ин- |
||||||
|
|
|
|
|||||
|
Ë1 |
|
|
Ë2 |
||||
|
|
|
терферометры для высокоточных из- |
|||||
|
Рис. 7.23 |
|
мерений расстояний, углов, показате- |
|||||
|
|
лей преломления сред или их измене- |
||||||
|
|
|
|
|
||||
ний и т. д. На рис. 7.23 показана схема интерферометра Рэлея, |
||||||||
предназначенного для измерения показателей преломления жид- |
||||||||
