
3323
.pdf
|
Вопросы для самопроверки |
|
|
1. |
Сформулируйте определение предела |
функции при |
|
x a |
и при x |
. Дайте геометрическую |
иллюстрацию |
определений этих пределов.
2.Что такое бесконечно малая и бесконечно большая величины? Какова связь между бесконечно большой и бесконечно малой величиной?
3.Каковы основные свойства бесконечно малых
величин?
4.Сформулируйте основные теоремы о пределах.
5.О чем говорится в первом замечательном пределе?
6.Как записываются основные формулы второго замечательного предела?
7.Какие бесконечно малые величины называются бесконечно малыми величинами одинакового порядка малости?
8.Приведите примеры эквивалентных бесконечно малых величин.
9.Дайте три определения непрерывности функции в
точке.
10.Перечислите типы точек разрыва функции и опишите каждый из них.
11.Каковы основные теоремы о непрерывных в точке функциях?
12.Сформулируйте свойства функций, непрерывных на
отрезке.
13.Какова геометрическая интерпретация теоремы о нуле непрерывной функции?
Задачи для самостоятельного решения
Вычислить пределы функций
31

1. |
lim |
|
x 2 |
|
5 |
(Ответ: |
9 |
). |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x |
2 x 2 |
|
4 |
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|||
2. lim |
|
x3 |
3x 2 |
|
2x |
(Ответ: |
|
|
2 |
). |
||||||||||||
|
|
x 2 |
|
x |
|
6 |
|
|
|
|
5 |
|||||||||||
|
x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
3. lim |
4x3 |
2x |
2 |
1 |
|
(Ответ: |
4 |
|
). |
|
|
|||||||||||
|
|
3x3 |
|
5 |
|
|
|
|
3 |
|
|
|
||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
4. |
lim |
4x3 |
2x |
2 |
|
x |
|
(Ответ: |
|
1 |
|
). |
|
|||||||||
|
|
3x 2 |
|
2x |
|
2 |
|
|
||||||||||||||
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
5. lim |
|
|
|
x 2 |
|
x |
|
(Ответ: 0). |
|
|
||||||||||||
|
|
|
3x 2 |
|
|
|
|
|||||||||||||||
|
x x 4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2x |
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||
6. lim |
|
|
|
|
|
|
|
|
|
(Ответ: |
2 2 |
). |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
x 4 |
|
|
x |
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
3 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7. lim |
|
|
|
|
1 |
x2 |
1 |
(Ответ: 0). |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
8. lim |
|
|
sin2 (x / 3) |
|
|
(Ответ: |
1 |
|
). |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
9 |
|
|
|
|
||||||||||||
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
9. lim |
|
tg2x |
|
(Ответ: |
2 |
). |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
x 0 sin 5x |
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|||||||||||
10. lim |
|
|
|
x |
|
|
1 |
|
|
2 x 1 |
(Ответ: e6 ). |
|||||||||||||||||||
|
|
|
x |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
11. lim |
|
|
|
2x |
3 |
|
x |
1 |
(Ответ: е). |
|||||||||||||||||||||
|
|
|
2x |
1 |
|
|
|
|
|
|
|
|||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
12. Найти точки разрыва функции y 1 21/ x |
||||||||||||||||||||||||||||||
график функции (Ответ: Разрыв второго рода при
( |
lim |
y |
, |
lim |
y 1)). |
x |
0 |
0 |
x |
0 |
-0 |
ипостроить
x0
32

|
-2 sin 2x, |
если |
|
x |
|
|
|
; |
|
|
|
||
|
2 |
|
|
||||||||||
13. Пусть f x |
Asin x B, |
если |
|
|
|
x |
|
|
; |
|
|
||
2 |
|
|
2 |
|
|
||||||||
|
cos x, |
если x |
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подобрать числа |
A и B так , чтобы функция |
f |
x была |
||||||||||
непрерывной ; построить еѐ график (Ответ: A |
1, |
B |
1). |
||||||||||
33

3. ПРОИЗВОДНАЯ ФУНКЦИИ И ЕЕ ПРИЛОЖЕНИЯ
3. 1. Дифференцируемость функции
Пусть |
имеется |
функция |
y |
f |
x , |
определенная |
и |
||||||||||
непрерывная в точке |
a |
и ее окрестности. Тогда некоторому |
|||||||||||||||
приращению аргумента |
x будет соответствовать приращение |
||||||||||||||||
функции |
y |
|
f a |
|
x |
f |
a . |
|
|
|
|
|
|
|
|
||
Функция |
y |
f |
x |
называется |
дифференцируемой |
в |
|||||||||||
точке |
|
a , |
если |
|
приращение |
функции |
y |
имеет |
вид |
||||||||
y A |
x |
|
x , |
где |
A является |
только функцией a |
и не |
||||||||||
зависит |
от |
|
x , |
а |
|
x -бесконечно малая величина более |
|||||||||||
высокого порядка |
малости |
по |
сравнению |
с |
приращением |
||||||||||||
аргумента |
x , т.е. lim |
|
x |
0 . |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
x |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|||
Главная |
линейная |
по |
x |
часть |
приращения функции |
||||||||||||
называется дифференциалом функции и обозначается
символом |
|
dy |
или |
df |
a . |
Дифференциалом |
независимой |
|||||||||||||||
переменной |
|
величины |
x является |
ее |
приращение |
x , |
т.е. |
|||||||||||||||
условно полагается , что dx |
x . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Рассмотрим предел отношения приращения функции |
y |
||||||||||||||||||||
к |
приращению |
аргумента |
x |
|
|
при |
x |
|
a |
|
|
для |
||||||||||
дифференцируемой функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
lim |
y |
lim |
A |
x |
x |
lim A |
|
x |
|
|
A |
lim |
|
|
x |
A . |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x |
|
x |
|
|
|
|
x |
|
x |
|||||||||||||
x a |
x a |
|
|
|
|
x a |
|
|
|
|
x a |
|
|
|||||||||
|
Величина |
A , |
определенная |
как |
|
предел |
отношения |
|||||||||||||||
приращения |
|
функции к |
приращению |
аргумента |
при |
|
x |
a |
||||||||||||||
( x |
0 ), играет очень важную роль, называется производной |
|||||||||||||||||||||
функции y |
|
f |
x по независимой переменной x при данном ее |
|||||||||||||||||||
значении |
x |
|
a |
и обозначается y , f |
a |
, |
|
dy |
или |
df a |
. Тогда |
|||||||||||
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
dx |
|
|
|
||
дифференциал |
dy |
записывается |
|
следующим |
|
образом: |
||||||||||||||||
34

dy = y dx . Операцию нахождения производной называют
дифференцированием.
Легко выяснить геометрический смысл производной и дифференциала функции. Введем сначала общее определение касательной к кривой. Возьмем на непрерывной кривой L две
точки M и M1 (рис. 12). |
|
|
|
|
|
|
|
|
|
|
|||
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dy |
M1 |
|
|
L |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
|
|
|
y |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
x |
x |
|
x |
|
|
|
||
|
|
|
Рис. 12. |
|
|
|
|
|
|
|
|||
Прямую |
MM1 , проходящую через эти точки, |
называют |
|||||||||||
секущей. Пусть точка M1 |
двигаясь |
вдоль кривой L , |
|||||||||||
неограниченно |
приближается |
к точке M . Тогда |
секущая, |
||||||||||
поворачиваясь |
около точки |
|
M , |
стремиться к |
некоторому |
||||||||
предельному положению . |
|
|
|
|
|
|
|
|
|
|
|||
Касательной к данной кривой в данной точке М |
|||||||||||||
называется предельное положение секущей MM1 , |
проходящей |
||||||||||||
через точку М, когда вторая точка пересечения |
M1 |
||||||||||||
неограниченно приближается по кривой к |
точке |
M . |
|||||||||||
Касательная к графику функции образует угол |
с осью Ох. |
||||||||||||
Секущая |
MM1 образует с |
осью |
Ox |
угол |
. |
Угловой |
|||||||
коэффициент секущей kсек = tg |
= |
|
y |
|
. При приближении точки |
||||||||
|
x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
M1 к точке |
M |
секущая, |
поворачиваясь около |
точки |
M , |
||||||||
переходит в касательную. Угол наклона касательной |
|
||||||||||||
стремится |
к углу |
наклона |
касательной |
, т.е. |
|
lim |
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
x a |
|
35

Поэтому угловой коэффициент касательной равен производной от ординаты y по абсциссе x
kкас |
tg |
limtg |
lim |
y |
|
y . |
|
x |
|||||||
|
|
x a |
x a |
|
|||
Из рисунка |
12 |
становится |
понятным |
геометрический |
|||
смысл дифференциала dy , представляющего приращение
ординаты касательной при переходе от точки a к точке a |
x . |
||||
Для выяснения физического смысла производной |
|||||
рассмотрим |
движение материальной точки |
по |
оси |
Oy . |
|
Координата |
материальной |
точки |
y |
является |
|
дифференцируемой функцией времени t . В момент времени t0 материальная точка имеет координату y t0 . В момент времени t0  t материальная точка приобрела координату y t0
t материальная точка приобрела координату y t0  t . Посчитаем среднюю скорость перемещения материальной
t . Посчитаем среднюю скорость перемещения материальной
точки за промежуток времени |
t |
|
|
|
|
|
|
Vср |
y t0 |
t |
y t |
|
|
y |
. |
|
t |
|
|
|
t |
||
|
|
|
|
|
|
||
Если устремить t к |
нулю |
и |
рассмотреть lim Vср , |
||||
|
|
|
|
|
|
|
t 0 |
равный мгновенной скорости материальной точки Vмгн , то
можно заметить, что lim V |
|
= lim |
y |
= |
dy |
, т.е. предел |
|
ср |
|
|
|||||
t 0 |
t 0 |
t dt |
|||||
|
|||||||
отношения приращения координаты материальной точки к приращению времени и есть с одной стороны производная координаты по времени, а с другой стороны - мгновенная скорость материальной точки.
Связь непрерывности и дифференцируемости функции устанавливается следующей теоремой.
Теорема. Если функция y f x дифференцируема в некоторой точке x0 , то она непрерывна в этой точке.
дифференцируема в некоторой точке x0 , то она непрерывна в этой точке.
Обратное утверждение неверно. Из того, что функция непрерывна в точке, не следует, что она дифференцируема, т.е.
36

непрерывная функция может не иметь производную в этой точке.
Например, функция f(x) определена на промежутке 0,  следующим образом (рис. 13):
следующим образом (рис. 13):
f (x) |
x, |
0 |
x |
1, |
|
2x 1, |
1 |
x |
. |
||
|
|
При x=1 функция непрерывна, так как |
|
lim |
f (x) |
lim f (x) f (1) 1 , но не дифференцируема. |
x 1 0 |
x |
1 0 |
y
|
|
y |
2x |
1 |
|
|
|
y x |
|
|
|
|
0 |
1 |
|
x |
|
|
|
Рис. 13. |
|
|
|
|
3.2. Правила дифференцирования |
|
|||
Теорема 1. Производная постоянной величины равна 0, |
|||||
т.е. если y c , где c |
const, то y |
0 . |
|
|
|
Теорема |
2. |
Производная |
суммы |
(разности) |
|
дифференцируемых функций равна сумме (разности) производных этих функций, т.е.
u x v x
v x u
u x
x v
v x .
x .
Теорема 3. Производная произведения двух дифференцируемых функций равна произведению производной первой функции на вторую плюс произведение производной второй функции на первую, т.е.
Теорема 4. Постоянный множитель можно выносить за знак производной, т.е.
cu x cu
cu x .
x .
37

Теорема 5. Производная частного двух дифференцируемых функций равна дроби, у которой знаменатель равен квадрату знаменателя, а числитель есть разность произведений производной числителя на знаменатель и производной знаменателя на числитель, т.е.
u x |
|
u x v x u x v x |
. |
|
|
||
v x |
|
v2 x |
|
3.3.Производная степенной, показательной
итригонометрических функций
|
|
|
1. Степенная функция y |
|
xn , n |
R . |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Найдем приращение функции |
|
y , придав аргументу x |
||||||||||||||||||||||||||||
приращение |
x : |
y |
|
x |
|
x n |
|
x n . Поэтому в соответствии с |
|||||||||||||||||||||||||
определением производной имеем: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x n |
|
x |
|
n |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|||||
|
x n |
|
|
|
|
y |
|
|
|
|
|
|
|
x |
x |
n |
x |
n |
|
|
x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
lim |
|
|
|
lim |
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|||||||||||||||
|
|
|
x |
0 |
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 |
|
|
|
x |
n |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
x |
n |
1 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x n |
|
|
|
|
|
x |
|
nxn 1 |
|
|
|
|
|
x |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
. |
|
||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||||||
|
|
|
x 0 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
x 0 |
|
|
|
|
n |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Покажем, что бесконечно малые величины |
|
|
|
|
||||||||||||||||||||||||||
1 |
x |
|
n |
1 |
|
|
и |
n |
|
x |
|
являются эквивалентными. Пусть |
|||||||||||||||||||||
x |
|
|
|
|
|
x |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x |
, а |
1 |
|
|
|
x |
n |
1 |
|
z , тогда |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
x |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
38

|
|
|
|
|
1 |
|
|
|
x |
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
1 |
|
|
n |
1 |
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
lim |
|
|
. |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x |
0 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
0 |
|
|
|
n |
|
|
|
|
|
|
0 n |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Поскольку |
|
|
|
|
1 |
n |
1 |
|
z , |
|
то |
|
z |
1 |
|
1 |
|
|
|
|
n , |
|
|
а |
||||||||||||||||||||||
ln 1 |
z |
|
n ln 1 |
|
|
|
|
. |
|
Так |
как |
|
бесконечно |
малая |
величина |
||||||||||||||||||||||||||||||||
ln 1 |
z |
|
эквивалентна |
величине |
z , |
а |
|
бесконечно |
|
малая |
|||||||||||||||||||||||||||||||||||||
величина ln 1 |
|
|
|
|
|
эквивалентна величине |
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
lim |
|
|
z |
|
|
|
|
lim |
|
ln 1 |
z |
|
lim |
n ln 1 |
|
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
0 n |
|
|
|
|
|
|
|
0 n ln 1 |
|
|
|
|
0 n ln 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Таким образом, производная степенной функции равна |
||||||||||||||||||||||||||||||||||||||||||||||
|
xn |
|
|
|
|
|
nxn 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
2. Показательная функция y |
|
a x , a |
|
0, a |
|
|
1. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
Найдем приращение функции |
y , придав аргументу x |
|||||||||||||||||||||||||||||||||||||||||||||
приращение |
|
x : |
|
y |
a x |
x |
a x . Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
a x |
|
|
|
|
|
|
lim |
|
|
|
y |
|
lim |
|
a x |
x |
a x |
|
a x lim |
|
|
a x |
1 |
. |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
В пределе перейдем к новой переменной |
y |
|
|
|
a x |
1 , |
||||||||||||||||||||||||||||||||||||||||
которая |
|
|
тоже |
|
|
|
является |
бесконечно |
|
малой |
величиной. |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
Используя |
|
второй |
замечательный |
предел |
lim 1 |
|
y |
|
|
|
e и |
||||||||||||||||||||||||||||||||||||
|
|
|
y |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
соотношение |
x |
|
|
log a 1 |
y , имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
a x |
lim |
|
a x |
|
1 |
a x lim |
|
|
|
|
y |
|
|
|
|
a x lim |
|
|
|
|
1 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||||
|
|
|
x |
0 |
|
|
|
|
|
x |
|
|
|
|
y |
0 log |
|
|
1 |
y |
|
|
|
|
y |
0 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
loga |
1 |
|
|
|
y |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
a x lim |
|
|
1 |
|
|
|
a x ln a . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
y |
|
|
|
0 log |
a |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
39
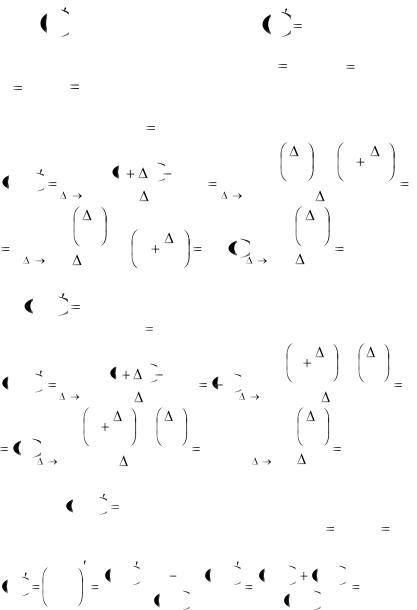
Таким образом, производная показательной функции равна
|
|
a x = ax ln a . При a = e имеем: e x |
|
|
|
|
|
e x . |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
3. Тригонометрические функции y |
|
sin x, |
y cos x , |
||||||||||||||||||||||||||||||||||||||||||||
y |
tgx, y |
|
ctgx. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Для функции y |
sin x имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 sin |
|
|
|
x |
|
|
cos x |
|
|
x |
|
||||||||||||
sin x |
|
|
lim |
sin x |
x |
|
|
|
sin x |
lim |
2 |
|
|
2 |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
sin |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
|
|
x |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 lim |
2 |
|
|
cos x |
|
|
|
cos x |
lim |
|
2 |
|
|
cos x , |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
x |
|
||||||||||||||||||||||||||||
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
т.е |
sin x |
|
cos x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
Для функции y |
cos x имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
|
x |
|
|
|
x |
|
sin |
|
|
x |
|
|||||||||
cos x |
|
|
lim |
cos x |
x |
|
|
cos x |
2 |
lim |
|
2 |
|
2 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
sin x |
|
|
|
x |
|
sin |
|
x |
|
|
|
|
|
|
|
sin |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
- 2 |
lim |
2 |
|
|
2 |
|
|
|
|
- sin x lim |
2 |
|
|
|
- sin x , |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
||||||||||||||||||||||||
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
т.е. cos x |
|
|
|
- sin x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Для нахождения производных функций y |
tgx, |
|
|
y ctgx |
|||||||||||||||||||||||||||||||||||||||||||
воспользуемся формулой производной частного: |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
tgx |
|
|
sin x |
|
|
|
|
|
sin x |
cosx |
sin x cosx |
|
|
cosx 2 |
|
|
sin x 2 |
1 |
|
|
. |
||||||||||||||||||||||||||||
|
|
cosx |
|
|
|
|
|
|
|
|
|
|
cosx 2 |
|
|
|
|
|
|
|
cosx 2 |
|
|
cos2 x |
|||||||||||||||||||||||||
40
