
3323
.pdf
2.ПРЕДЕЛ. НЕПРЕРЫВНОСТЬ ФУНКЦИИ
2.1Предел функции
Число A называется пределом функции y f x при x ,
при x ,
стремящемся к а ( x a ), если для любого сколь угодно малого положительного ε > 0 найдется такое δ(ε) > 0, что для всех х,
удовлетворяющих |
|
|
неравенству |
|
x |
a |
|
|
|
|
имеет |
место |
|||||||||||||||||
неравенство |
|
|
f |
x |
|
A |
|
. |
Если |
A |
есть |
предел |
функции |
||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||
y |
f |
x при x |
a , то пишут |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim f |
|
x |
A . |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение |
|
предела |
|
функции |
|
y |
f |
x |
графически |
||||||||||||||||||
иллюстрируется следующим образом (рис. 1). |
|
|
|
||||||||||||||||||||||||||
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
А+ |
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
А- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а- |
|
а |
|
а+ |
|
|
|
|
|
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1. |
|
|
|
|
|
|
|
|
||||
|
|
Для сколь угодно малой |
|
-окрестности около ординаты |
|||||||||||||||||||||||||
A найдется такая |
|
|
|
окрестность точки a , что для всех точек |
|||||||||||||||||||||||||
x |
из |
|
окрестности точки a |
точки графика функции y f x |
|||||||||||||||||||||||||
будут лежать внутри полосы шириной |
2 |
, |
ограниченной |
||||||||||||||||||||||||||
прямыми y |
A |
ε, |
|
y |
|
A ε . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Число |
A называется пределом функции |
y |
f x |
при x , |
|||||||||||||||||||||||
стремящемся к бесконечности, если для любого сколь угодно малого положительного ε > 0 найдется такое N , что для всех
11

x |
N будет выполняться |
неравенство |
|
f x |
A |
|
, что |
||||
|
|
||||||||||
записывается следующим образом |
|
|
|
|
|
|
|
||||
|
|
lim |
f |
x |
A . |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
Определение |
предела |
функции |
y |
f x |
при |
x |
||||
графически иллюстрируется следующим образом (рис. 2). |
|||||||||||
|
y |
|
|
|
|
|
|
|
|
|
|
|
А A+ |
|
|
|
|
|
|
|
|
|
|
|
A- |
|
|
|
|
|
|
|
|
|
|
|
О |
|
|
N |
|
|
|
x |
|
|
|
|
|
Рис. 2. |
|
|
|
|
|
|
|
||
|
Для сколь угодно малой |
-окрестности около ординаты |
|||||||||
A |
найдется такое |
значение |
|
N , |
что |
для |
всех |
x N график |
|||
функции не будет выходить за пределы полосы шириной 2 .
2.2.Бесконечно малые и их основные свойства |
||||
Функция |
y |
(x) |
называется |
бесконечно малой |
величиной при |
x |
a , если |
lim (x) 0 , |
т.е. для любого сколь |
|
|
|
x a |
|
угодно малого ε > 0 найдется такое δ(ε) > 0, что для всех x ,
удовлетворяющих |
неравенству |
x a |
, |
имеет место |
||
|
|
|
|
|
|
|
неравенство |
x |
|
. |
|
|
|
Любая константа, какой бы малой она ни была, не является бесконечно малой величиной.
12

|
Пример 2.1. Функция |
1 |
будет бесконечно малой при |
||||
|
|
x |
|||||
|
|
|
|
|
|
||
x |
, так как lim |
1 |
0 . |
Действительно, из определения |
|||
x |
|||||||
|
x |
|
|
|
|
||
предела следует, что для любого наперед заданного произвольно малого положительного найдется такое число N, что для всех значений х, удовлетворяющих неравенству |x| > N,
|
1 |
0 |
. Имеем |
1 |
|
, |
| x | |
1 |
, тогда N |
|
1 |
, |
| x | |
N |
|
|
1 |
. |
|
|||||
|
x |
|
x |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Теорема |
1. |
|
|
Если |
lim |
f x A , |
то |
( f |
x |
|
A ) |
|
есть |
|||||||||
|
|
|
|
|
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
бесконечно малая величина, и наоборот, |
если |
f x |
|
|
A |
|
x , |
|||||||||||||||||
где |
x - бесконечно малая величина, то lim f |
x |
A . |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
a |
|
|
|
|
|
|
|
|
|
|
|
Теорема 2. Сумма конечного числа бесконечно малых |
||||||||||||||||||||||
величин есть величина бесконечно малая. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
Теорема 3. Произведение любого числа бесконечно |
|||||||||||||||||||||
малых величин есть бесконечно малая величина. |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Теорема 4. Произведение бесконечно малой величины и |
|||||||||||||||||||||
ограниченной функции есть бесконечно малая величина. |
|
|
||||||||||||||||||||||
|
|
|
Следствие 2. Произведение бесконечно малой величины |
|||||||||||||||||||||
на константу есть бесконечно малая величина. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Функция |
y |
|
|
f |
x |
называется |
бесконечно |
|
большой |
||||||||||||
величиной при |
x |
|
|
a , если для любого сколь угодно большого |
||||||||||||||||||||
числа M найдется такое |
0, зависящее от |
M , что для всех |
||||||||||||||||||||||
|
x |
из |
- окрестности будет выполняться условие |
|
f x |
|
M , |
|||||||||||||||||
|
|
|
||||||||||||||||||||||
что записывается следующим образом |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
lim |
f x |
. |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Теорема |
4. |
|
Если |
x |
является |
|
бесконечно |
малой |
|||||||||||||
величиной, то |
1 |
|
есть бесконечно большая величина. |
|
|
|||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
x |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13

|
|
|
|
2.3. Основные теоремы о пределах |
|
|||||||||
Рассмотрим пределы функций при |
x a , полагая, |
что |
||||||||||||
результаты не изменятся и при x |
|
. |
|
|
|
|||||||||
Теорема 1. Предел алгебраической суммы функций u x |
||||||||||||||
и v x |
равен алгебраической сумме пределов этих функций. |
|
||||||||||||
lim u x |
v x |
|
lim u x |
lim v x . |
|
|
||||||||
x |
|
a |
|
|
|
x a |
|
x |
a |
|
|
|
||
Пример 2.2. |
|
|
|
|
|
|
|
|
|
|||||
lim |
|
5x2 |
6x |
lim |
5 |
6 |
lim 5 |
lim |
6 |
5 . |
|
|||
|
x2 |
|
|
x |
x |
|
||||||||
x |
|
|
|
|
x |
|
x |
|
x |
|
|
|||
Теорема |
2. |
Предел |
|
произведения |
|
функций u x |
и |
|||||||
v x равен произведению пределов этих функций.
|
lim u x |
v x |
|
|
lim u x |
lim v x . |
||||||
|
x |
a |
|
|
|
x a |
|
|
x |
a |
|
|
|
Следствие. Постоянный множитель можно выносить за |
|||||||||||
знак предела: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
cv x |
c lim v x . |
|||||||
|
|
|
x a |
|
|
|
|
|
x |
a |
|
|
|
Теорема 3. Предел частного от деления двух функций |
|||||||||||
u x |
и v x равен частному от деления пределов этих функций |
|||||||||||
|
|
|
|
|
u x |
|
|
lim u x |
|
|||
|
|
|
lim |
|
|
|
x a |
|
. |
|||
|
|
|
|
v x |
|
lim v x |
||||||
|
|
|
x a |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
x a |
|
|
|
Теорема 4. |
Если |
lim |
f |
x |
A , |
а функция y принимает |
|||||
|
|
|
x a |
|
|
|
|
|
|
|
|
|
неотрицательные значения |
y |
0 , |
то |
A есть неотрицательное |
||||||||
число A 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 5. Если между соответствующими значениями |
|||||||||||
двух |
функций u |
u(x) и |
v=v(x) |
|
выполняется неравенство |
|||||||
u(x) |
v(x) и lim u(x) |
u0 , |
|
lim v(x) |
v0 , |
|
то имеет место |
|||||
|
x a |
|
|
|
x |
a |
|
|
|
|
|
|
неравенство u0 |
v0 . |
|
|
|
|
|
|
|
|
|
|
|
14

Теорема |
6. |
|
Если |
lim |
u(x) |
|
u0 , |
lim v(x) |
u0 |
и |
|||||||||||
|
|
|
|
|
|
|
x |
a |
|
|
|
x |
a |
|
|
|
|
|
|||
u(x) z x |
v(x) , то |
lim z(x) |
u0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
x a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема 7. Если функция |
y |
f |
x |
|
при |
x |
|
a |
|
является |
|||||||||||
неубывающей и ограничена сверху числом M , т.е. |
|
f |
x |
|
M , |
||||||||||||||||
|
|
||||||||||||||||||||
то функция y |
f x |
|
имеет предел при x |
|
a . |
|
|
|
|
|
|
|
|
|
|||||||
Пример 2.3. Вычислить предел lim |
7x2 |
2x |
. |
|
|
|
|
|
|
||||||||||||
|
3x 4 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
x |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
7x |
2 |
2x |
|
|
lim 7x2 |
2x |
|
7 lim |
x2 |
2 lim |
x |
|
9 |
|
|
|
||||
lim |
|
|
x 1 |
|
|
x 1 |
|
|
x 1 |
|
|
. |
|
|
|||||||
3x4 |
1 |
|
|
lim 3x4 |
1 |
|
3lim x |
4 lim 1 |
2 |
|
|
||||||||||
x 1 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
x 1 |
|
|
x 1 |
|
|
x |
1 |
|
|
|
|
|
|
|
|
Если при вычислении пределов алгебраической суммы, произведения или частного от деления функций сами функции стремятся к некоторым константам, не равным одновременно нулю в случае деления функций, то вычисление пределов как в предыдущем примере не вызывает затруднения. Пределы отношения бесконечно малых величин, отношения бесконечно больших величин, произведения бесконечно малой и бесконечно большой величины в зависимости от частного закона изменения рассматриваемых величин могут принимать различные значения или даже не существовать. Выражения
вида |
|
0 |
, |
|
|
|
, 0 |
, |
, 1 |
|
|
называются |
||
0 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
неопределенностями. |
|
|
|
|
|
|
|
|
||||||
2.4. Предел функции |
|
sin x |
при x |
0 |
|
|||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
(первый замечательный предел) |
|
|
|||||||||||
Функция |
y |
|
sin x |
не |
определена при |
x |
0 . Найдем |
|||||||
|
|
|
|
|
||||||||||
|
|
x |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
предел этой |
функции |
|
при |
x |
0 . Рассмотрим |
окружность |
||||||||
радиуса R . Пусть острый центральный угол MOA равен x .
15

|
|
|
|
|
|
|
|
|
|
|
|
|
|
М |
|
|
|
|
|
С |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
х |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
О |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
Рис. 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Из рис. 3 следует, |
|
что |
|
площадь |
треугольника |
MOA |
|||||||||||||||||||||||||||
S MOA, площадь сектора |
|
MOA Ssekt , |
|
площадь |
треугольника |
||||||||||||||||||||||||||||
COA S COA связаны неравенством |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
S MOA |
Ssekt |
|
S COA. |
|
|
|
|
|
|
|
||||||||||||||||||
Поскольку |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
S MOA |
AO MB |
|
|
R R sin x |
|
R2 sin x |
|
, Ssekt |
|
R2 x |
|
, |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
S COA |
OA CA |
|
R |
R |
tgx R 2tgx |
, |
|
|
|
|
|
|
||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
то имеем |
|
|
R 2 sin x |
|
|
R 2 x |
|
|
|
R |
2tgx |
|
. |
|
|
|
|
|
|
|
|||||||||||||
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Разделим все члены на выражение |
|
R 2 sin x |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
x |
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
sin x |
|
|
|
cos x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Перейдем к обратным величинам, воспользовавшись |
|||||||||||||||||||||||||||||||||
свойствами неравенств, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
1 |
|
sin x |
|
|
|
cos x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Так как |
lim cos x |
|
1, lim 1 |
1, а переменная величина |
sin x |
|
|||||||||||||||||||||||||||
x |
|||||||||||||||||||||||||||||||||
|
x 0 |
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
заключена между двумя величинами, имеющими предел равный 1, то на основании теоремы 6 предыдущего параграфа
16

|
|
|
|
|
|
|
|
|
lim |
sin x |
1. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример 2.4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
lim |
sin 3x |
lim |
sin 3x |
3 |
5x |
|
|
3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x 0 sin 5x |
x 0 |
3x 5 |
sin 5x |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Пример 2.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin |
2 3x |
|
|
|
|
|
|
|
|
|
|
|
|||
lim |
1 cos3x |
lim |
2sin2 3x 2 |
|
2 lim |
|
|
2 |
|
|
|
4x2 |
|
|
|
9 4 x2 |
9 |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
sin2 2x |
|
|
9 4 x2 |
|
|
sin2 2x |
|
|
|
4x2 |
|
|
|||||||||||||
x 0 sin2 2x |
x 0 |
|
|
x 0 |
|
|
|
|
|
|
8 |
|
|||||||||||||||||
|
2.5. Число e. Второй замечательный предел |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
||
|
Рассмотрим |
|
переменную |
|
величину |
1 |
|
|
|
. Можно |
|||||||||||||||||||
|
|
|
|
x |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
показать, что эта переменная величина возрастает и ограничена. Следовательно, она должна иметь предел. Действительно,
|
1 |
x |
|
|
lim 1 |
|
|
e , |
|
|
x |
|
||
x |
|
|
|
|
где e - иррациональное число (e |
2,71828 ...) . |
|
||
Если в равенстве положить 1/x = , то при x |
имеем |
|||
0 и получаем |
|
|
|
|
lim 1 |
1/ |
=е. |
|
|
|
|
|
||
0 |
|
|
|
|
При решении конкретных задач на пределы могут быть полезны модифицированные варианты записи второго замечательного предела:
|
1 |
x |
|
|
|
1 |
|
x |
|
|
lim 1 |
e |
, |
lim |
1 |
|
|
e , |
|
||
|
|
|
|
|
||||||
x |
x |
|
|
|||||||
x |
|
|
x 0 |
|
|
|
|
|||
где x является бесконечно большой величиной, |
а |
x - |
||||||||
бесконечно малой величиной при x |
a , или при x |
|
. |
|
||||||
17

Пример 2.6.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
1 |
6 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
lim |
1 |
|
|
|
|
|
|
|
= lim |
1 |
|
|
|
|
1 |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
1 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= |
|
lim |
1 |
|
|
|
|
|
|
|
|
|
|
lim |
|
1 |
|
|
|
|
|
|
|
|
= е 1=е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
Пример 2.7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
lim |
1 |
|
1 |
|
3x |
|
= lim |
|
1 |
|
1 |
|
x |
1 |
|
1 |
x |
1 |
|
1 x |
= |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|
x |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= lim |
|
|
1 |
1 |
|
|
x |
lim |
|
|
1 |
|
1 |
|
|
|
x |
lim |
|
|
|
1 |
1 |
|
x |
|
= е |
е е = |
e3. |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
x |
|
|
|||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
Пример 2.8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
x 3 x 3 |
|
|
|
|
|
|
|
|
|
|
x 1 4 x 3 |
|
|
|
|
|
|
|
|
4 |
|
|
|
x 3 |
|
|||||||||||||||||||||||||
lim |
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
x |
|
1 |
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
|||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
x |
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
4 |
|
4 |
|||
= lim |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
1 |
|
|
|
|
|
|
|
|
|
|
lim |
1 |
|
= |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
x |
|
1 |
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
x 1 |
||||||||||||||||||||||||||||||||||||
|
4 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
0 |
|
|
|
|
|
|
|
|
4 |
|
0 |
|
|
|
|
|
||||||||||||||||||
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= lim |
1 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
1= e 4 |
1 |
|
e 4 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
x |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
4 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2.6. Раскрытие некоторых неопределенностей |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Рассмотрим |
предел |
|
функции lim |
|
f (x) |
|
|
(или |
при x |
), |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
a |
|
g(x) |
|
|
|
|
|
|
|
|
|||||||
который при непосредственной подстановке x |
= a |
приходит к |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
одному из случаев неопределенности. Укажем приемы для решения таких примеров, приемы «раскрытия неопределенности».
18
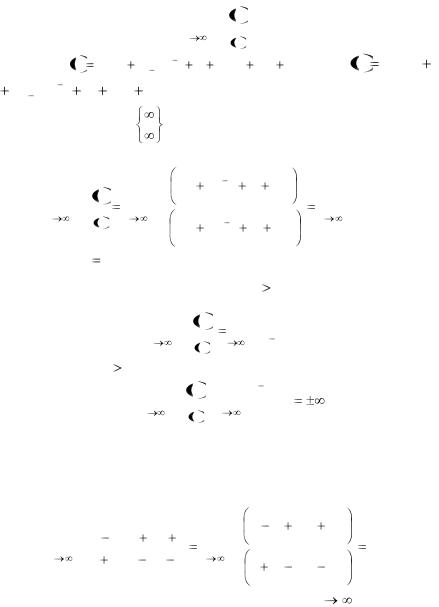
1.Рассмотрим предел отношения многочленов при x 
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
Pn x |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qm x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
где |
|
|
P |
|
x |
a |
n |
xn |
|
a |
n 1 |
xn 1 ... |
|
|
a |
2 |
x |
2 |
|
|
|
a x a |
0 |
, |
|
|
Q x |
|
|
|
b x m |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
||||||||||||
|
|
b |
|
x m 1 ... |
|
|
b x |
|
b . |
|
|
|
Для |
|
|
|
|
раскрытия |
|
получающейся |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
m 1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
неопределенности |
|
|
|
|
|
|
|
|
|
|
необходимо |
вынести |
|
x в |
|
старшей |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
степени в числителе и знаменателе |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
n |
an |
|
an 1 |
|
|
|
|
... |
|
|
a0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
lim |
|
|
Pn |
x |
|
|
|
|
lim |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
xn |
|
|
|
|
lim |
|
xn an |
|
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
Qm x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
bm 1 |
|
|
|
|
|
|
|
b0 |
|
|
|
|
|
x mb |
|
||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
x |
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
bm |
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Если m |
|
|
n , |
то предел равен отношению коэффициентов |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
при старших степенях |
an |
. Если же m |
|
n , то |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
bm |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
Pn |
x |
|
|
|
|
|
lim |
|
an |
|
|
=0. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qm x |
|
|
x |
|
x m |
|
|
nb |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
В случае n |
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
x |
|
|
|
|
|
|
|
|
|
xn m a |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
n |
|
|
= lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qm x |
|
|
|
|
bm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где |
|
|
знак |
|
|
|
|
|
бесконечности |
|
|
|
|
|
|
|
|
определяется |
|
|
|
знаком |
||||||||||||||||||||||||||||||||||||||||
коэффициента |
an |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
bm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Пример 2.9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
7 |
4 |
|
|
|
|
|
2 |
|
1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
lim |
|
7x3 |
|
|
4x 2 |
|
|
2x 1 |
|
lim |
|
|
|
|
|
|
x |
|
|
|
|
x2 |
|
x3 |
|
|
|
7 |
. |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3x |
3 |
|
|
|
4x |
2 |
|
6x |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
6 |
|
8 |
|
|
|
|
3 |
|||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x 2 |
|
x3 |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
Здесь было |
|
использовано, |
|
|
что |
|
при x |
|
|
|
|
|
величины |
|||||||||||||||||||||||||||||||||||||||||||||
|
1 |
, |
1 |
, |
1 |
|
стремятся к нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
x |
x2 |
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
19

2. Если в пределе многочлены в числителе и знаменателе
стремятся к нулю, то получается неопределенность вида |
0 |
, |
|
0 |
|||
|
|
для раскрытия которой надо разложить числитель и знаменатель на множители и сократить одинаковые бесконечно малые величины.
Пусть a является действительным корнем кратности многочлена, стоящего в числителе, т.е.
|
Pn x |
x a Pn x , где Pn a 0 . |
Кроме |
того, |
a является действительным корнем |
кратности |
многочлена знаменателя, т.е. |
|
Qm x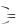 x a
x a Qm
Qm x , где Qm
x , где Qm a
a 0 .
0 .
Если |
= |
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
lim |
|
Pn |
x |
lim |
x a Pn |
x |
|
|
|
|
|
Pn |
a |
. |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x a Qm x x a x a Q |
x |
|
|
|
|
|
Qm |
a |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
|
|
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
lim |
|
Pn x |
|
|
lim |
|
x a Pn |
|
x |
|
|
|
Pn |
|
a |
lim |
x a |
0 . |
||||||||||||||||
|
Qm x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Qm |
|
a |
||||||||||||||||
x a |
|
x a x a Q |
|
x |
|
|
|
|
x a |
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
|
|
|
, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
lim |
Pn x |
|
lim |
|
x a Pn |
|
x |
|
|
|
Pn |
a |
|
|
lim |
|
|
1 |
|
. |
||||||||||||||
Qm x |
|
|
|
|
|
|
|
|
|
|
|
|
Qm |
a |
|
|
|
|
|
|
||||||||||||||
x a |
x a x a Q |
m |
|
x |
|
|
|
|
x a x a |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2.10. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
lim |
|
|
x3 |
|
2x2 |
|
x |
|
lim |
|
x(x2 |
2x 1) 1 |
. |
|
|
|
|
|
||||||||||||||||
|
|
|
x2 |
|
|
|
|
|
|
|
x(x 2) |
|
|
2 |
|
|
|
|
|
|
||||||||||||||
x 0 |
|
2x |
|
|
|
x 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Пример 2.11. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
lim |
|
x3 |
|
4x2 |
5x 2 |
lim |
|
|
|
x 1 2 (x 2) |
0 . |
|
|
|||||||||||||||||||||
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x 1 |
|
2x 3 |
|
|
|
x 0 x 1 (x2 |
x 3) |
|
|
|
||||||||||||||||||||||||
20
