3323

x sin xdx

u

x,

du

dx

x cos x

cos x dx

dv

sin xdx, v

cos x

0

0

0

sin x

0

.

Вычислить

определенный

интеграл

Пример

8.5.

e

x ln xdx.

1

Решение:

u

ln x,

du

dx

e

x

x2 ln x

e

e x2 dx

x ln xdx

x2

1

2

2x

1

dv

xdx,

v

1

2

e

2

x

2

e

e

2

e

2

1

e

2

1

.

2

4

1

2

4

4

4

4

8.8. Замена переменной в определѐнном интеграле

b

Пусть

для

вычисления

интеграла

f ( x)dx ,

где

f(x) –

a

некоторая

непрерывная функция,

требуется

сделать

замену

x

(t) .

1)

функция x

t и

ее

производная

x

t

непрерывны на отрезке

,

,

2)

множеством

значений

функции x

t

при

t

, является отрезок

a, b ,

b

f (x)dx

f (t) (t)dt .

a

При

вычислении

определенного

интеграла,

Пример

8.6.

Вычислить

определенный

интеграл

1

x 2

1

x 2 dx.

0

Решение:

x

sin t

1

dx

costdt

2

x 2

1

x 2 dx

x1

0, t1

0

sin2 t

1

sin2 t cost dt

0

0

x2

1, t2

2

2

sin2 t cos2 t dt

1

2

sin2 2t dt

1

2

1

cos4t

dt

4

8

0

0

0

1

t

/ 2

1

sin 4t

/ 2

0

.

0

0

8

4

16

16

8

dx

Пример 8.7. Вычислить определенный интеграл

.

3

0

1

x

Решение:

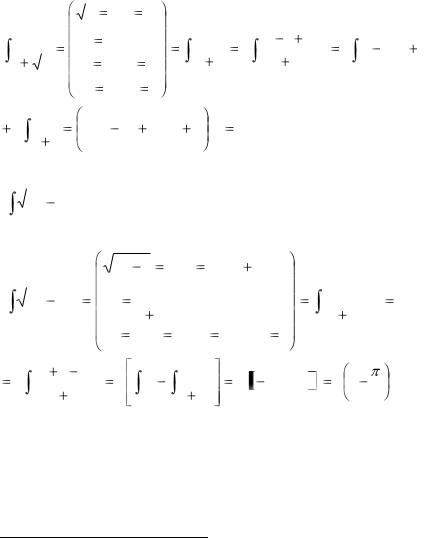
t 3

3 x

t, x

8

dx

dx 3t 2 dt

2 3t 2 dt

2 t 2

1 1

2

3

dt 3

(t 1)dt

0 1

3 x

x1

0, t1

0

0 1 t

t 1

0

0

x2

8, t2

2

2 dt

3t 2

2

30

3t

3ln

t

1

0

3ln 3.

t

1

2

Пример8.8.

Вычислить

определенный

интеграл

ln 2

e x

1dx.

0

Решение:

e x

1

t,

x

ln(t 2 1)

ln 2

2t

1

2t

e x

1dx

dx

dt,

t

dt

1 t 2

1 t 2

0

0

x1

0, t1

0, x2

ln 2, t2

1

1

t 2

1

1

1

1

dt

1

2

dt 2

dt

2 t

arctgt

2 1

.

t 2

1

1 t

2

0

4

0

0

0

a, , и выделим отрезок a, N .

Несобственным

интегралом

от функции f x по

бесконечному промежутку a,

называют предел интеграла

по промежутку a, N

при N

:

N

f (x)dx

lim

f (x)dx .

a

N

a

Пример 8.9. Вычислить несобственный интеграл

dx

.

1

x 2

xdx

N

xdx

1

N

lim

lim

ln

x 2

1

1 x

2

1

x

2

1

2

N

N

1

1

1

lim

ln N 2

1

ln 2

.

2 N

O a

x

a

a

f ( x)dx

lim

f ( x)dx .

N

N

Если f(x) непрерывна на всей числовой оси, то

a

f (x)dx

f (x)dx

f (x)dx .

a

В этом случае интеграл

f (x)dx сходится, если сходятся

поэтому

используются

признаки

сходимости

для

несобственных интегралов первого рода.

Теорема. (Признак сравнения) Если на промежутке a,

непрерывные функции

x

и

f x

подчиняются неравенству

0

x

f x , то из сходимости интеграла

f (x)dx

следует

a

сходимость интеграла

(x)dx , а из расходимости интеграла

a

(x)dx следует расходимость интеграла

f (x)dx .

a

a

Пример

8.11.

Исследовать на сходимость

интеграл

dx

.

1

x2 1

e x

Решение: Сравним данный интеграл с известным

сходящимся

интегралом

dx

.

Так

как

при

1

x 2

x

1

1

1

,

то

dx

dx

.

x2 1 e x

x2

1 x 2 1 e x

1 x 2

Следовательно, интеграл сходится.

Теорема.

Если

существует

предел

lim

f

x

k ,

x

x

0

k

f

x

0,

x

0 ,

то

интегралы

f (x)dx

и

a

x3

11

ln

dx .

1

x3

5

Решение: Рассмотрим для сравнения интеграл

dx

1

x3

N dx

1

1

1

lim

lim

1

.

Поскольку интеграл

x

1 x3

2 x

N 2

2

сравнения

сходится,

а

ln

x3

11

ln(1

6

)

6

lim

x3

5

lim

x3

5

lim

x3 5

6 , то сходится

1

x

x

1

x

1

x3

x3

x3

O a

b

x

b

Тогда, если существует конечный предел lim

f x dx ,

0

a

непрерывна на промежутке

a,b , а при x

a имеет разрыв II

рода, тогда

b

b

f (x)dx

lim

f (x)dx.

a

0 a

Если функция y

f x

испытывает разрыв второго рода

во внутренней точке c отрезка

a, b , то несобственный

интеграл второго рода определяется формулой

b

c

b

f

x dx

f x

dx

f

x dx .

a

a

c

Если

f x 0 , то несобственный интеграл второго рода

b

f x

dx

интерпретируется

геометрически

как площадь

a

бесконечно высокой криволинейной трапеции.

Для

несобственных

интегралов

второго

рода

используются признаки сходимости.

Теорема. Если на промежутке

a,b

функции

f x

и

x

непрерывны, а при

x

b испытывают разрыв второго

рода

и

удовлетворяют

условию

0 f

x

x ,

то

из

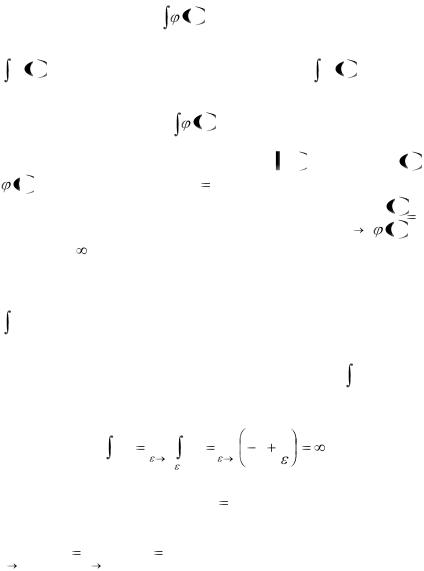
b

сходимости интеграла

x dx

следует сходимость интеграла

a

b

b