
3323
.pdf
6. КОМПЛЕКСНЫЕ ЧИСЛА
6.1. Основные понятия
Среди действительных чисел не существует решений алгебраических уравнений с отрицательными значениями дискриминанта. Возникшая в математике потребность дополнить множество действительных чисел так, чтобы содержались все решения алгебраических уравнений, была
удовлетворена введением мнимой единицы ί 
 1 . Математический символ ί обозначает одно из решений
1 . Математический символ ί обозначает одно из решений
уравнения x2 1 0 и определяется соответствующими правилами действия над ним. Числа вида bί , где b является действительным числом, называются чисто мнимыми. Однако, наиболее общими числами, составленными с помощью мнимой
единицы, являются комплексные числа z a |
ί b , где a |
и b - |
|||
действительные числа. |
|
|
|
|
|
Комплексными |
числами |
называются |
выражения |
||
z a ί b , где a и |
b -действительные |
числа, а |
ί – |
||
математический символ, который называется мнимой единицей: i2= 1.
Первая компонента a комплексного числа z a ί b
называется его действительной или вещественной частью и
обозначается a Re z . Вторая компонента b называется мнимой частью комплексного числа z a ί b и обозначается b Im z .
Комплексные числа имеют достаточно простой геометрический смысл. Выберем на плоскости декартову прямоугольную систему координат. Тогда каждой паре чисел (a,b) будет соответствовать на плоскости Oxy точка с
абсциссой a и ординатой b , рассматриваемая как геометрический образ комплексного числа z a ί b . Можно сказать, что каждому комплексному числу z a ί b будет соответствовать определѐнная точка (a,b) плоскости Oxy и,
91

наоборот, каждой точке (a,b) плоскости Oxy будет отвечать
определѐнное комплексное число z a ί b . Между множеством комплексных чисел и множеством точек плоскости Oxy существует взаимно однозначное соответствие.
Плоскость Oxy называется плоскостью комплексных чисел z . Действительные числа изображаются при этом точками оси Ox , которая называется действительной или
вещественной осью.
Чисто мнимые числа z  ί b изображаются точками на оси Oy , которая называется мнимой осью.
ί b изображаются точками на оси Oy , которая называется мнимой осью.
Комплексное число z a ί b можно отождествить и с радиус-вектором, начало которого совпадает с началом координат, а конец – с точкой (a,b) .
6.2. Три формы записи комплексного числа
Запись комплексного числа в виде z x iy называется алгебраической формой представления комплексного числа z .
|
Два |
комплексных |
числа z1 |
x1 |
ί y1 |
и |
z2 |
x2 |
ί y2 |
||||||||||
равны друг другу тогда и только тогда, когда x1 |
x2 и y1 |
y2 . |
|||||||||||||||||
|
Если |
|
x1 |
x2 , |
а |
y1 |
y2 , |
то |
комплексные |
числа |
|||||||||
z1 |
x1 |
ί y1 |
|
и |
z2 |
x1 |
ί y1 называются |
комплексно |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
сопряжѐнными: |
z |
x1 |
ί y1 , z |
x1 |
ί y1 . |
|
|
|
|
||||||||||
|
Точки, соответствующие комплексно сопряженным |
||||||||||||||||||
|
|
|
|
|
|
||||||||||||||
числам z |
и z , симметричны относительно действительной оси |
||||||||||||||||||
Ox . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тригонометрическая форма записи комплексных чисел |
||||||||||||||||||
появляется |
|
в |
результате |
представления |
радиус-вектора |
||||||||||||||
r |
OM |
x, y , |
соответствующего |
|
|
|
комплексному |
числу |
|||||||||||
z |
x |
ί y |
в полярной системе координат. Длина вектора r , |
||||||||||||||||
изображающего |
комплексное |
число |
|
z , называется |
модулем |
||||||||||||||
комплексного числа и обозначается |
|
z |
|
или r . Величина угла |
|||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
92

между положительным направлением действительной оси и
радиус-вектором |
r |
называется |
аргументом |
этого |
|||||
комплексного числа, и обозначается Arg z или |
. Аргумент |
||||||||
комплексного |
числа |
z |
0 |
не |
определен. |
Аргумент |
|||
комплексного |
числа |
Arg z |
- величина |
многозначная, |
|||||
определяется с точностью до слагаемого 2k |
(k |
1,0,1,2,3...) : |
|||||||
Arg z =arg z + 2k |
, |
|
|
|
|
|
|
|
|
где arg z -главное |
значение |
аргумента, |
заключенное в |
||||||
промежутке |
, . |
|
|
|
|
|
|
|
|
Проекции |
|
радиус-вектора |
r , |
изображающего |
|||||
комплексное число |
z |
x |
ί y , |
равны |
x r cos |
и y |
r sin |
||
(рис.24). Следовательно, комплексное число z |
можно записать |
||||||||
в виде, называемом тригонометрической формой записи
комплексного числа
z r cos |
|
ir sin |
|
r(cos |
i sin |
) . |
|
|
|||
|
y |
|
|
|
|
|
M |
|
|||
|
|
|
|
|
|
|
|
|
|||
|
y |
|
|
|
r |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ |
|
|
|
|
||
|
O |
|
|
|
|
|
x |
x |
|||
|
|
|
|
|
Рис.24. |
|
|
|
|||
Модуль комплексного числа определяется однозначно |
|||||||||||
формулой |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
|
z |
|
x 2 |
y 2 . |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
Например, |
|
i |
|
02 |
12 1. Аргумент |
определяется из |
|||||
|
|
||||||||||
формул |
|
|
|
|
|
|
|
|
|
|
|
cos rx , sin
rx , sin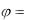 ry , tg
ry , tg xy .
xy .
93

Так как |
< argz < , то из соотношения |
tg |
y |
|
|
||||
x |
||||
|
|
|
||
следует, что |
|
|
|
arctg xy , для I, IV четвертей, argz arctg xy  , для II четверти, arctg xy
, для II четверти, arctg xy  , для III четверти.
, для III четверти.
Если точка z расположена на действительной или мнимой оси, то argz находится непосредственно. Например,
для z 5 argz 0 , а для z |
3 ί |
argz |
|
|
. |
2 |
|||||
Два комплексных числа |
z1 |
и z2 |
равны тогда и только |
||
тогда, когда равны их модули, а аргументы равны или отличаются на 2кπ:
|
|
|
z1 |
|
|
z2 |
, 1 |
2 |
|
2k |
k 0, |
1, |
2,... . |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 6.1. Записать комплексное число |
z |
1 |
|
3 ί в |
||||||||||||||||||||||||
тригонометрическом виде. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
1 2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||
Решение: |
z |
|
r |
|
3 |
2, |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
argz arctg |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
2 |
|
|
|
2 |
. |
|
|
|
|
|
|
|||||||||||
Поэтому z |
1 |
|
|
3 ί= 2 cos |
|
i sin |
|
|
|
|
|
|
||||||||||||||||
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Использование |
формулы |
|
|
|
Эйлера |
ei |
= cos |
|
i sin |
|||||||||||||||||||
позволяет перейти от тригонометрической формы записи комплексного числа к показательной или экспоненциальной форме:
94

|
|
|
|
|
z |
r ei , |
где r = |
z |
|
- |
модуль |
комплексного числа, а угол |
|
Argz |
|
argz |
2k ( k |
0, 1, |
2... ). В силу формулы Эйлера |
|
функция |
ei |
является периодической с основным периодом |
||||
2 . |
|
|
|
|
|
|
Пример 6.2. Записать комплексное число z  1 ί в показательном виде.
1 ί в показательном виде.
|
|
|
|
|
|
|
|
1 2 |
1 2 |
|
|
|
|
|
Решение: |
|
z |
r |
|
2, |
|||||||
argz |
arctg |
1 |
|
|
|
|
|
|
3 |
. Поэтому |
|||
1 |
|
|
4 |
|
4 |
||||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
ei . |
|
|
|
|
|
|
|||
z |
1 ί= |
2 |
|
|
|
|
|
|
|
||||
6.3. Действия над комплексными числами
На множестве комплексных чисел определены действия, аналогичные действиям, определенным на множестве действительных чисел.
Суммой двух комплексных чисел z1 x1 iy1 и
z2 x2 iy2
называется число, определяемое равенством
z1 z2 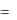 x1 x2 i y1 y2 ,
x1 x2 i y1 y2 ,
т.е. при сложении комплексных чисел их действительные и мнимые части складываются. Сложение комплексных чисел
обладает |
переместительным |
(коммутативным) |
и |
||
сочетательным (ассоциативным) свойствами: |
|
||||
|
z1 |
z2 |
z2 |
z1, |
|
|
z1 z2 |
z3 |
z1 |
z2 z3 . |
|
Из вышеприведенного определения следует, что сложение комплексных чисел производится подобно сложению векторов (рис.25).
95

y |
z1 z2 |
z2
z1
O |
x |
Рис.25
Вычитание комплексных чисел определяется как действие, обратное сложению. Разностью двух комплексных
чисел z1 |
x1 |
iy1 |
и z2 |
x2 |
iy2 |
называется число z1 |
z2 , |
|||||
определяемое равенством |
|
|
|
|
|
|
|
|||||
|
|
|
|
z1 z2 = x1 |
x2 |
|
i y1 |
y2 . |
|
|
|
|
|
Геометрически комплексные числа вычитаются как |
|
||||||||||
векторы, т.е. при вычитании комплексных чисел их |
|
|
||||||||||
действительные и мнимые части вычитаются. |
|
|
|
|||||||||
|
Пример 6.3. Вычислить z |
z1 |
z2 |
z3 , если z1 |
3 |
4i , |
||||||
z2 |
2 6i , z3 |
1 5i . |
|
|
|
|
|
|
|
|
||
|
Решение: |
z |
3 |
2 1 |
4 |
6 5 i = 4 3i . |
|
|
|
|||
|
Произведением двух комплексных чисел z1 |
x1 |
iy1 |
и |
||||||||
z2 |
x2 |
iy2 называется комплексное число, определяемое |
||||||||||
равенством |
|
|
|
|
|
|
|
|
|
|
||
|
z1z2 |
x1 |
iy1 x2 |
iy2 |
x1x2 |
y1 y2 |
i x1 y2 |
x2 y1 . |
|
|||
Произведение комплексных чисел в алгебраическом представлении производится по обычным правилам перемножения алгебраических многочленов с учетом того, что
i 2 |
1, i3 i 2i |
i и т.д. |
Пример.6.4. Вычислить произведение 4 7i 3 5i .
96

Решение: |
|
|
|
|
|
|
|
|
|
|
4 7i 3 |
5i 1`2 20i |
21i |
35i 2 |
12 |
35 |
i |
47 |
i . |
||
Следует |
отметить, |
что |
|
|
|
|
|
|
|
x2 y2 |
z z |
x |
iy |
x |
iy |
||||||
является действительным числом, равным квадрату модуля
комплексного числа. |
|
|
|
Умножение |
комплексных |
чисел |
подчиняется |
переместительному, сочетательному и распределительному законам
|
|
z1z2 |
|
z2 z1, |
|
|
|
|
|
|
|
z1 z2 z3 |
|
z1 z2 z3 , |
|
|
|
|
|
||
|
z1 z2 |
z3 |
|
z1 z2 |
z1 z3 . |
|
|
|
|
|
Если комплексные числа заданы в тригонометрической |
|
|||||||||
форме: |
|
|
|
|
|
|
|
|
|
|
z1 |
r1 cos 1 |
i sin 1 |
и z2 |
r2 |
cos |
2 |
isin |
2 , |
||
то произведение комплексных чисел равно |
|
|
|
|
|
|||||
z1 z2 |
r1 cos 1 |
i sin |
1 r2 |
cos |
2 |
isin |
2 |
|
||
r1r2 cos 1 cos 2 |
sin |
1 sin |
2 |
i sin 1 cos 2 |
cos 1 sin |
2 |
||||
r1r2 |
cos |
1 |
2 |
i sin |
1 |
2 . |
|
|
|
|
Отсюда вытекает правило, что при перемножении комплексных чисел модули их перемножаются, а аргументы складываются.
При перемножении комплексных чисел в показательной форме вышеуказанное правило сохраняется, т.е.
|
|
|
|
|
z z |
2 |
r r ei |
1 |
2 . |
|
|
||
|
|
|
|
1 |
|
1 2 |
|
|
|
|
|
||
Пример 6.5. Найти произведение комплексных чисел |
|||||||||||||
z1 1 i и z2 |
|
|
i , предварительно перейдя к |
|
|
||||||||
3 |
|
|
|
||||||||||
тригонометрическому представлению. |
|
|
|
|
|||||||||
Решение: z1 |
|
|
|
|
|
|
|
|
|
, z2 |
|
|
|
1 |
i |
2 cos |
|
|
i sin |
|
|
3 i |
|||||
|
|
|
|
||||||||||
|
|
|
|
|
|
4 |
4 |
|
|
|
|
||
97

2 cos |
|
|
|
|
i sin |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
6 |
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
z1 z2 |
2 2 |
|
cos |
|
|
|
|
|
i sin |
|
|
|
2 2 cos |
|
|
i sin |
|
|
||||||
|
|
6 |
|
|
6 |
|
|
|||||||||||||||||
|
|
|
|
|
4 |
|
|
|
4 |
12 |
|
12 |
||||||||||||
Деление комплексных |
чисел определяется как операция, |
|||||||||||||||||||||||
обратная операции умножения. Частным от деления двух комплексных чисел z1 и z2 0 называется комплексное число z , которое, будучи умноженным на z2 , дает число z1 , т.е.
z1 |
z , если z z2 |
z1 . |
|
z2 |
|||
|
|
Практически деление комплексных чисел в алгебраическом представлении производится посредством умножения числителя и знаменателя на число, комплексно сопряженное знаменателю:
z1 |
|
|
x1 |
|
iy1 |
|
x1 |
iy1 x2 |
iy2 |
|
|
x1x2 |
y1 y2 |
|
i y1x2 x1 y2 |
|
||||||||
z2 |
|
|
x2 |
|
iy2 |
|
x2 |
iy2 x2 |
iy2 |
|
|
|
|
|
x22 |
|
y22 |
|||||||
|
Пример 6.6. Выполнить деление |
1 |
|
i |
. |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3i |
|
|
|
|
|
||
|
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 i |
|
|
|
1 i 2 3i |
2 3i |
|
2i |
3 |
|
|
1 |
|
5i |
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 3i |
2 3i 2 3i |
4 9 |
|
|
13 13 |
|
||||||||||||||||
|
При |
делении |
комплексных |
чисел |
z1 и |
z2, заданных в |
||||||||||||||||||
тригонометрической форме, модули комплексных чисел делятся, а аргументы вычитаются. По определению:
z |
zz |
2 |
|
z |
|
z |
|
z |
2 |
|
z |
|
|
|
z1 |
|
, |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
z2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Arg z1 Arg z |
|
Arg z2 |
|
Arg z |
Arg z1 |
|
Arg z2 . |
||||||||||
Модуль частного двух комплексных чисел равен частному модулей этих чисел, а аргумент частного равен разности аргументов делимого и делителя.
98

z1 |
|
r1 |
cos |
|
|
i sin |
|
|
. |
z2 |
|
r2 |
1 |
2 |
1 |
2 |
|||
|
|
|
|
||||||
|
|
|
|
|
|
|
|
В показательном представлении операции с модулями и аргументами комплексных чисел при делении совпадают с таковыми при делении в тригонометрическом виде:
z1 |
|
r1 |
ei 1 2 . |
z2 |
|
r2 |
|
|
|
Возведение комплексного числа в целую положительную степень является распространением правила умножения комплексных чисел на случай, когда все n множителей одинаковы. В алгебраическом представлении возведение комплексного числа в n -ую степень производится по алгебраическим правилам перемножения многочленов с учетом того, что
i2 |
1, i3 |
i2i |
i, i4 |
i3i 1. |
В тригонометрическом представлении модуль n -ой степени комплексного числа равен n - ой степени модуля исходного комплексного числа, а аргумент n -ой степени комплексного числа получается посредством умножения на n аргумента исходного комплексного числа. В итоге получается
формула Муавра:
|
z n r n cosn |
i sin n . |
|
|
|
|
||
В показательном представлении имеем: |
|
|
|
|
||||
|
z n |
r n ein . |
|
|
|
|
||
|
|
|
i 12 . |
|
|
|
|
|
Пример 6.7. Вычислить ( |
3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Решение: |
Запишем |
|
|
число |
z |
3 i |
в |
|
тригонометрическом |
виде, |
учтя |
|
при |
|
этом, |
|
что |
||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
12 2 , |
arctg |
|
|
|
|
|
|
|
|
|
|
|||
r |
3 |
|
|
, |
z |
2 cos |
|
i sin |
|
. |
||||||||
|
|
|
|
6 |
6 |
6 |
||||||||||||
|
3 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Произведя по указанным правилам возведение в двенадцатую степень комплексного числа, имеем
99

|
|
|
|
|
|
|
12 |
12 |
|
12 |
|
|
|
|
|
|
|
212 cos |
|
212. |
|||||
( |
3 |
i 12 |
2 cos |
|
i sin |
|
i sin |
|||||
|
|
|
|
|
||||||||
|
|
|
6 |
6 |
|
6 |
|
6 |
|
|||
Извлечение корня n - степени определяется как действие, обратное возведению в натуральную степень. Корнем n-ой степени из комплексного числа z называется такое
комплексное число w , что выполняется равенство wn z . Если комплексные числа z и w представлены в
тригонометрической форме |
|
z r cos i sin и w |
cos i sin , |
то, по определению корня и формуле Муавра, получаем z wn  n cosn
n cosn i sin n
i sin n r cos
r cos i sin .
i sin .
Согласно определению два комплексных числа равны, если равны их модули, а аргументы равны или отличаются на
|
|
n r |
|
|
|
|
|
|
||
четное число , поэтому |
или |
n r , а n |
2k |
, |
||||||
k 0, |
1, 2,... или |
|
2k |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
n |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
В |
результате определению |
корня |
n ой |
степени |
из |
|||||
комплексного числа удовлетворяю n комплексных чисел, описываемых формулой
|
|
|
|
|
n |
|
|
|
|
|
2k |
|
|
|
2k |
|
|
|
n r cos |
i sin |
|
r cos |
|
|
i sin |
. |
|
||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
n |
|
n |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Операция |
извлечения |
корней |
|
n |
ой |
степени |
из |
|||||||||||
комплексного |
числа |
оказывается |
многозначной, т.е. |
n |
||||||||||||||
значениям |
параметра |
k |
|
|
k |
0,1,2,..., n 1 |
соответствуют |
n |
||||||||||
различных значений аргумента |
k , а поэтому и |
n значений |
||||||||||||||||
самого корня |
n ой |
|
степени |
из |
|
комплексного числа. |
||||||||||||
Остальным |
целым |
k |
|
|
|
соответствуют |
|
значения |
k , |
|||||||||
отличающиеся от одного из указанных значений на величину, кратную 2π и не дающие новых значений корня.
Таким образом, комплексное число z 0 имеет ровно n корней степени n, получаемых из вышеприведенной формулы. Следует отметить, что все значения корня лежат на
100
