
Методы оптимизации в примерах и задачах. Медведь Н.А., Фокин А.А
.pdf
Н.А. Медведь А.А. Фокин
МЕТОДЫ ОПТИМИЗАЦИИ В ПРИМЕРАХ И ЗАДАЧАХ
x2
1
x*
x1
Воронеж 2003
3
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Воронежский государственный технический университет
Международный университет высоких технологий
Н.А. Медведь А.А. Фокин
МЕТОДЫ ОПТИМИЗАЦИИ В ПРИМЕРАХ И ЗАДАЧАХ
Утверждено редакционно-издательким советом университета в качестве учебного пособия
Воронеж 2003
4
УДК 517.8
Медведь Н.А., Фокин А.А. Методы оптимизации в примерах и задачах: Учеб. пособие. Воронеж: Воронеж. гос. техн. ун-т, 2003
152с.
В учебном пособии содержится краткий теоретический материал и указания по использованию методов оптимизации в решении задач математического программирования. Пособие предназначено для индивидуальных занятий студентов специальностей 220300 “Системы автоматизированного проектирования” и 190500 “Биотехнические и медицинские аппараты и системы” по дисциплинам “Оптимизация в САПР”, “Методы оптимизации” всех форм обучения.
Учебное пособие подготовлено на магнитном носителе в текстовом редакторе Microsoft Word и содержится в файле doс.
Табл.: 43, Ил.: 24, Библиогр.: 18 назв.
Научный редактор д-р техн. наук, проф. Я.Е. Львович
Рецензенты: кафедра дифференциальных уравнений Воронежского государственного университета; д-р техн. наук, проф. Г.И. Лозгачев
© Медведь Н.А., Фокин А.А., 2003 © Оформление. Воронежский
государственный технический университет, 2003
5
ВВЕДЕНИЕ
Поиск оптимального, а не любого допустимого решения характеризует современный уровень проектирования в САПР. Методы и средства решения оптимизационных задач приобретают исключительно важное значение в качестве механизма организации и математического обеспечения процесса проектирования. В связи с этим для студентов технических специальностей необходимы знания возможностей применения математических методов и ЭВМ, а также понимания проблем, возникающих при их использовании.
Данное учебное пособие ориентировано на тех, кто хочет использовать методы оптимизации как инструмент решения конкретных прикладных задач, не имеет практически никаких знаний в области математического программирования, однако имеет представление о функциях n переменных и знаком с правилами и приемами программирования.
Пособие дает довольно полное представление о подходе к решению задач оптимизации с ограничениями и без ограничений. В начале каждого параграфа пособия приводятся определения, формулы и другие краткие теоретические сведения и методические сведения, необходимые для решения приведенных задач. Кроме того, в книге можно найти подробное описание алгоритмов небольшого числа ставших уже классическими методов математического программирования. Все описанные методы проиллюстрированы большим числом примеров с краткими пояснениями теоретических положений. В каждом параграфе приводятся задачи для самостоятельного решения и ответы к ним. Большинство задач носит условный характер, а числовые параметры подобраны так, чтобы при решении задач можно было обойтись наиболее простыми вычислениями.
В учебное пособие вошли далеко не все алгоритмы оптимизации. Для тех, кто захочет расширить знания по теории оптимизации, познакомиться с другими типами задач математического программирования, кроме изложенных в настоящей книге, ниже приводится список дополнительной литературы.
6

I. ЭКСТРЕМУМЫ ФУНКЦИИ
1.1. Условия экстремума функции одной переменной
Пусть |
функция |
y f (x) |
определена на |
некотором |
|
множестве |
X |
R и |
обладает |
некоторыми |
свойствами |
дифференцируемости (гладкости). |
|
|
|||
Точка |
x0 |
X доставляет локальный максимум |
(минимум) |
||
функции f (x) , если существует такая δ-окрестность точки x0 , что
для всякой точки x x0 |
этой окрестности выполняется неравенство |
|||||||||||||
|
|
f (x) f (x0 ) ( f (x) f (x0 )). |
|
|
|
|
|
|
|
|||||
Напомним, что δ-окрестностью |
U (x0 ) точки |
|
х0 |
|
называется |
|||||||||
открытый промежуток ] x0 |
, x0 |
[ с центром в точке x0 . Точки |
||||||||||||
максимума и минимума называются точками экстремума. |
|
|
|
|||||||||||
|
Необходимое условие локального экстремума. |
Если |
x0 |
– |
||||||||||
точка локального экстремума функции |
f (x) |
и |
f |
' (x ) |
существует, |
|||||||||
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f ' (x) 0. |
|
|
|
|
|
|
|
|
|
|
|
||
|
Точки, в которых производная равна нулю, называются |
|||||||||||||
стационарными точками функции. |
|
|
|
|
|
|
|
|
|
|
||||
|
Достаточные условия локального экстремума. |
|
|
|
|
|||||||||
|
Первый |
достаточный признак. |
Если |
|
f (x) |
имеет |
||||||||
производную на каждом из интервалов ]x0 |
, x0[ |
и ]x0 , x0 |
[ , где |
|||||||||||
- |
некоторое |
положительное |
число, |
и |
f ' (x) |
|
0 ( |
0) при |
||||||
x ]x |
, x [ , |
f ' (x) |
0 (>0) при |
x |
]x , x |
|
[ , |
то |
x |
-точка |
||||
0 |
0 |
|
|
|
|
0 |
0 |
|
|
|
|
0 |
|
|
максимума (минимума). |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Второй достаточный признак. Пусть функция y |
|
f (x) |
|
||||||||||
|
а) дифференцируема в точке |
х0 |
и |
в |
некоторой |
еѐ |
||||||||
окрестности; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7
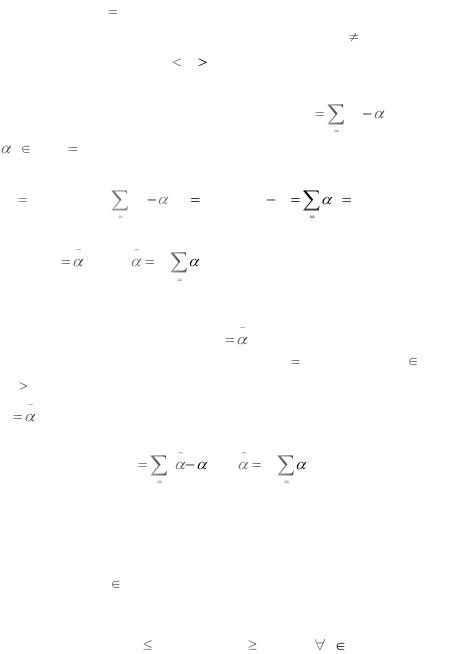
|
б) |
f ' (x ) |
0 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в) имеет вторую производную f '' (x ) и |
f |
'' (x ) |
|
0 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
Тогда, если |
f |
'' (x ) |
0( 0) , то точка х0 – точка максимума |
|||||||||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
(минимума). |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
Пример 1. Найти экстремумы функции |
y |
|
(x |
k |
)2 |
, где |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k 1 |
|
|
|
|
k |
R, k |
1, 2,..., n. |
|
|
|
|
|
|
|
|
|
|
|
||
|
Решение. Найдем стационарные точки. Из условия |
|
|
||||||||||||
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
y' |
0 следует |
2 |
(x |
|
|
k |
)2 0 или nx y |
|
k |
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
k |
1 |
|
|
|
|
|
k |
1 |
|
|
|
|
|
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
1 |
|
n |
|
|
|
|
|
|
|
|
, |
где |
|
|
|
|
k . |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
n k 1 |
|
|
|
|
|
|
||
Так как функция дифференцируема на всей оси, то экстремальные точки следует искать лишь в стационарных точках, т.е. в нашем
случае в ”подозрительной” точке x |
. |
|
|
|
|
||||
|
Вычислим вторую производную |
|
y'' |
2n . Для всех x R |
|||||
y'' |
0 . Поэтому по второму достаточному признаку заключаем, что |
||||||||
x |
является точкой минимума рассматриваемой функции и |
||||||||
|
n |
|
|
)2 |
|
1 n |
|
|
|
|
y |
( |
k |
, |
|
|
k |
. |
|
|
|
|
|||||||
|
min |
|
|
|
n k |
|
|||
|
k |
1 |
|
|
|
1 |
|
||
Замечание. Этот результат используется в математической статистике при отыскании оценок по методу наибольшего правдоподобия.
Точка |
x0 R доставляет глобальный максимум (минимум) |
функции f (x) |
на множестве X , если |
|
f (x) f (x0 ) , ( f (x) f (x0 )), x X. |
8
Если f (x) непрерывна на некотором замкнутом промежутке
[a,b] и дифференцируема на ]a,b[ ,то для отыскания глобальных экстремумов необходимо найти все локальные экстремумы на ]a,b[ , вычислить граничные значения f(a) и f(b) и выбрать среди этих чисел наибольшее и наименьшее. Это и есть глобальный максимум и глобальный минимум функции f(x) на [a,b].
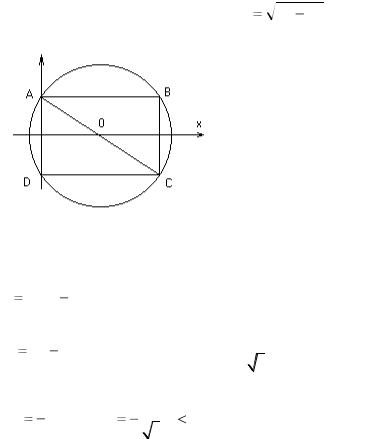
Пример 2. Из бревна с круглым сечением диаметра d требуется изготовить балку прямоугольного сечения. Подобрать ширину b и высоту h этого сечения так, чтобы балка оказывала наибольшее сопротивление при работе на изгиб.
Указание. В сопротивлении материалов установлено, что при
работе на изгиб прочность прямоугольной балки пропорциональна bh2.
Решение. Введем обозначения АВ=х, АС=d, AD 
 d 2 x2
d 2 x2
(рис. 1.1.1).
Рисунок 1.1.1
По условию задачи необходимо найти глобальный максимум функции
y x(d 2 x2 )
на [0, d] . Найдем стационарные точки:
y' |
d 2 3x2 ; так как |
|
y' =0, то x |
|
= |
1 |
|
d. |
||
0 |
|
|
|
|||||||
|
||||||||||
|
|
|
|
|
3 |
|
|
|||
|
|
|
|
|
|
|
|
|||
Вычислим вторую производную в точке x0 : |
|
|
|
|
|
|
||||
y'' |
6x , y'' (x ) |
6 |
d 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
0 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9

d
Итак, в точке x0  искомая функция имеет максимум.
искомая функция имеет максимум.
 3
3
Этот максимум глобальный, так как y(0) = y(d) = 0.
Ответ: b |
1 |
|
|
d, h |
|
2 |
|
d . |
|||
|
|
|
|
|
3 |
||||||
3 |
|||||||||||
|
|
|
|
|
|
||||||
Замечание. |
В |
строительном деле обычно предписывается |
|||||||||
отношение h : b = 7 : 5. Это и есть приближенное значение 
 2 1, 4.
2 1, 4.
Задачи для самостоятельного решения
Найти глобальные экстремумы следующих функций:
1.1.1. |
y |
ax2 |
|
bx |
|
c, |
|
(a |
0), |
x |
R ; |
||||||||
1.1.2. |
y |
|
x |
, |
|
x |
|
R ; |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
|
x2 |
|
|
|
||||||||||||||
1.1.3. |
|
y |
|
3x4 |
|
6x2 , x |
[ |
2, 2]; |
|||||||||||
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
1.1.4. |
|
y |
xe |
2 |
|
, |
|
x |
|
R ; |
|
|
|
||||||
|
|
|
|
|
1 |
|
|
|
|
|
( x |
a )2 |
|
|
|
|
|||
1.1.5. |
|
y |
|
|
|
e |
|
|
2 |
, |
x |
R , a |
const . |
||||||
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
1.1.6. Определить размеры открытого бассейна с квадратным дном объемом 32 м3 так, чтобы на облицовку его стен и дна пошло наименьшее количество материала.
1.1.7.Для хранения и охраны военного имущества требуется огородить забором прямоугольный участок площадью S=1,5 га и затем таким же забором разделить этот участок на две равные части. Определить размеры участка, при которых расход материалов будет наименьшим.
1.1.8.Штаб инженерной части планирует строительство тоннеля с сечением в форме правильной трапеции площадью 5 м2 и
сострым углом при нижнем основании, равным α. Определить размеры сечения тоннеля, при которых расход материалов на боковые стенки и потолок был бы минимальным.
1.1.9.Два самолета летят в одной плоскости и прямолинейно
под углом 1200 с одинаковой скоростью км/час. В некоторый момент один самолет пришел в точку пересечения линий движения,
10
а второй не дошел до неѐ d км. Через сколько времени расстояние между самолетами будет наименьшим? Чему равно это расстояние?
1.1.10.Из трех досок одинаковой ширины сколачивается желоб. При каком угле наклона боковых стенок площадь поперечного сечения желоба будет наибольшей?
1.1.11.На параболе y = x2 найти точку, наименее удаленную от прямой y = 2x - 4.
1.1.12.Балка прямоугольного сечения со свободно опертыми концами равномерно нагружена по всей длине. Стрела ее прогиба обратно пропорциональна моменту инерции сечения балки
I |
|
1 |
xy3 , |
|
12 |
||||
|
|
|||
где x и y – размеры балки. Определить размеры балки при наименьшей стреле прогиба, если балка вырезана из круглого бревна
сдиаметром D.
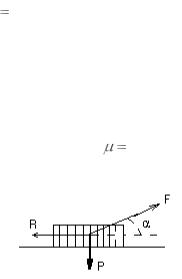
1.1.13.Груз весом Р, лежащий на горизонтальной плоскости, нужно сдвинуть приложенной к нему силой F (рис. 1.1.2). Под каким углом α к горизонту нужно направить силу F, чтобы она была
наименьшей. Коэффициент трения |
0, 25. |
Рисунок 1.1.2
1.1.14.Сечение тоннеля имеет форму прямоугольника, завершенного полукругом. Периметр сечения 18 м. При каком радиусе полукруга площадь сечения будет наибольшей?
1.1.15.В данный шар вписать цилиндр с наибольшим
объемом.
1.1.16.Из круглого листа вырезать такой сектор, чтобы, свернув его, получить воронку наибольшей вместимости.
1.1.17.Однородный стержень АВ, который может вращаться около точки А (рис. 1.1.3), несет груз Q кг на расстоянии d см от точки А и удерживается в равновесии вертикальной силой Р,
11

приложенной к свободному концу В стержня. Погонный сантиметр стержня висит q кг. Определить длину стержня х так, чтобы сила Р была наименьшей и найти Pmin.
Рисунок 1.1.3
1.1.18. Каноническая воронка, радиус основания которой R, а высота H, наполнена водой. В воронку погружается шар. Каким должен быть радиус шара r, чтобы объем воды, вытесненной из воронки погруженной частью шара, был наибольшим?
1.2. Экстремум функции многих переменных. Условный экстремум. Метод Лагранжа
Пусть на множестве D Rn , где Rn - арифметическое n – мерное пространство, задана числовая функция
u=f(P).
Здесь Р(х1,х2,…xn) – точка Rn , принадлежащая D.
Функция u f (P) имеет локальный максимум (минимум) в точке P0 (x10 , x20 ,..., xn0 ) , если существует такая окрестность точки Р0,
для всех точек Р(х1,х2,…xn) которой, не совпадающих с Р0, выполняется неравенство
f (P0 ) f (P) ( f (P0 ) f (P)) .
Необходимое условие локального безусловного экстремума.
Если дифференцируемая функция u f (P) имеет в точке P0 экстремум, то в этой точке
12
