Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3172

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

3.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1612 13 14 15 16 > Следующая >>>

задаче, и y0 , допустимый в двойственной задаче, такие, что

cT x0 bT y0 , то x0 - решение исходной, а y0 - решение

двойственной задачи.

Теорема 1. (Первая теорема двойственности) Если одна из задач (двойственная или исходная) имеет решение, то и двойственная к ней имеет решение, причем оптимальные значения целевых функций совпадают.

Теорема 2. (Вторая теорема двойственности) Для того,

чтобы допустимая в исходной задаче точка x0 и допустимая в двойственной задаче точка y0 являлись соответственно

решениями исходной и двойственной задач, необходимо и достаточно, чтобы выполнялись равенства (условия дополняющей нежесткости)

a y0

1, n

или (x0 )T (c

AT y0 )

0 ;

a y0

1, m

или ( y0 )T (b

Ax0 )

0 .

Замечание 1. B симплекс - процедуре осуществляется перебор базисов В (невырожденных) подматриц исходной матрицы А таким образом, что


1.		На каждой итерации метода вектор xB		x , где
			0
		B 1b , является допустимым в исходной задаче, т.е.
	x	B 1b , является допустимым в исходной задаче, т.е.
AxB b , xB 0 ;
2.		На заключительной итерации, кроме случая, когда

получена оптимальная точка, оценки всех векторов Aj неотрицательны:

cT B 1 A c 0 , j 1, n

j B j j

или

cBT B 1 A yT A AT y c ,

т.е. вектор cBT B 1 является допустимым в двойственной

113

задаче, кроме того, он является решением двойственной задачи. При этом часть ограничений двойственной задачи

выполняется в виде равенств ( AT y) j c j , j I , где I - множество базисных индексов (так как оценки базисных

векторов всегда равны нулю	j	0, j I ). Такие точки у
	j

называются базисными в двойственной задаче.

Пример 1. На основании графического анализа двойственной задачи исследовать разрешимость следующих задач, и в случае разрешимости найти оптимальное значение целевой функции.

à) 6x1	9x2 3x3				min		á) 2x1	x2	2x3		min
x1	2x2		x3	3,			x1	x2	x3	2,
3x1	x2	x3		1,			x1	3x2	2x3		1,
x1	0,	x2		0, x3		0.	x1	0,	x2	0,	x3 0.
â) 5x1	x2	x3	x4		max
4x1	x3	x4	16,
6x1	4x2	x3		x4	4,
x1	0, x2		0,	x3	0,	x4	0.

Решение.

а) Двойственная задача будет иметь вид:

3y1	y2		max
y1	3y2		6,
2 y1	y2		9,
y1	y2	3,
y1	0,	y2	0.

Графическое решение данной задачи (рис. 4.5.1) показывает,

что Y *	(4,1)	с z*	13.
max		max

114

x2	2
	2
	1
	3
	y*
	x1
Рисунок 4.5.1 – Графическое решение задачи

В силу первой теоремы двойственности исходная задача также имеет решение, причем оптимальное значение равно 13.

б) Двойственная задача будет иметь вид:

2 y1	y2	max
y1	y2	2,
y1	3y2	1,
y1	2 y2	2.

Графический анализ показывает (рис. 4.5.2), что двойственная задача неразрешима из-за неограниченности целевой функции, поэтому по свойству 3 исходная задача неразрешима из-за пустоты допустимого множества.

x2 1

Рисунок 4.5.2 – Неограниченная целевая функция

115

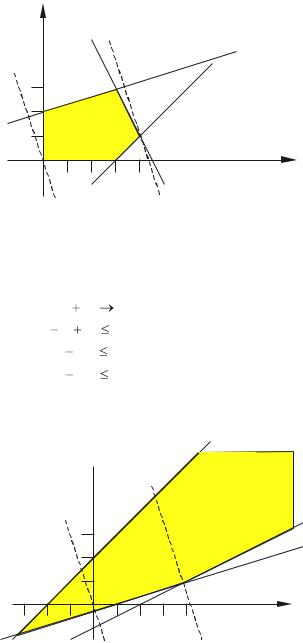
в) Двойственная задача запишется в виде:
16 y1		4 y2		min
4 y1		6 y2		5
4 y2		1
y1	y2		1
y1	y2		1
y1 , y2		0.
Графический анализ этой задачи показан на рис.4.5.3.
y2
				y1
				y*
Рисунок 4.5.3 – Графическое решение двойственной задачи

Оптимальным		решением	является вектор Y *		13	,	1	,

			min	8			4

zmin*	25 . На	основании	второй теоремы двойственности				для

вектора х*, являющегося решением исходной задачи, должны выполняться равенства

x1* (4 y1*		6 y2* 5) 0 ,	x3* ( y1*		y2*	1) 0,
x* ( 4 y*		1) 0 ,	x* ( y*		y*	1) 0 .
2	2		4	1	2

Подставляя координаты вектора Y *		, получаем, что переменные x
	min	3
и x4	исходной задачи должны обращаться в ноль. Тогда из исходной
системы получаем 4x1 16 , откуда		x1 4 , и 6x1 4x2 4 , откуда
x2	5 . Следовательно, решением исходной задачи является вектор
	116

Xmax*	(4,5,0,0) . При этом zmax*	5* 4 5 25 .
	Задачи для самостоятельного решения

Решить следующие задачи, используя решение двойственных задач симплекс – методом:

4.5.1 6 x1	+ 4 x2		min,	4.5.2	2 x1	+	3 x2	min,
2 x1	+	x2	3,		x1	+	5 x2	16,
x1 –		x2	1,		3 x1	+	2 x2	12,
– x1 + 2 x2			1;		2 x1	+	4 x2	16;
4.5.3 –6 x1 – 4 x2			max,	4.5.4	6 x1	+	4 x2	min,
2 x1 + x2			3,		2 x1 + x2			3,
x1 – 2 x2			2,		3 x1 + 2 x2			1,
3 x1 + 2 x2			1;		– x1 – x2			6;
4.5.5 7 x1	+	x2	min,	4.5.6	7 x1	+ 10 x2		min,
x1	+	x2	3,		2 x1	+	28 x2	17,
5 x1 + x2			5,		x1 + 2 x2			3;
x1	+ 5 x2		5;		x1	+ 17 x2		19;

4.5.7	x1 + x2 + 2 x3		min,
	2 x1 – x2 – 3 x3 + x4			= – 3,
	x1 – 3 x2 – 4 x3		+ x5 = – 1;
4.5.8 –15x1 – 33 x2			max,	4.5.9	x1	+ 2 x2	min,
	3 x1 +	2 x2	6,		2 x1	+ x2	18,
	6 x1 +	x2	6;		x1	+ 2 x2	14,
					x1 – 2 x2		10;

117

4.5.10 78 x1	+	52 x2	min, 4.5.11	5 x1	+ 4 x2		min,
6 x1 +		2 x2	9,	x1 + x2			6,
10 x1 + 14 x2			13,	2 x1	+	x2	9,
11 x1		x2	6;	3 x1	+	x2	11.

4.6. Задача линейного программирования транспортного цеха


			ЗЛП транспортного цеха формулируется следующим
образом: пусть имеется m пунктов отправления						A1 , A2 ,…, Am , в
которых сосредоточен однородный груз, и				n пунктов назначения
B1 ,		B2 ,…, Bn . Заданы количество груза ai , i
					1, m в каждом пункте
Ai	и размеры спроса каждого пункта bj , j
				1, n в одних и тех же

единицах измерения. Известна также матрица C						(cij ) , i 1, m ,

j	1, n расходов cij на перевозку единицы продукции из пункта Ai

в пункт Bj . Необходимо определить такой план перевозки, который

бы обеспечивал вывоз всех грузов из пунктов отправления, удовлетворение всех потребностей в пунктах назначения и имел бы минимальную стоимость.

В случае, если выполняется равенство

m	n
ai	bj (условие баланса),
i 1	j 1

задача называется закрытой транспортной задачей. В противном случае – открытой.

Для разрешимости транспортной задачи необходима и достаточна еѐ закрытость.

Математическая постановка закрытой транспортной задачи имеет следующий вид:

m n

cij xij min

(4.6.1)

i 1 j 1

при ограничениях

118

xij

ai ,

i 1, m ;

(4.6.2)

j 1

xij

bj ,

1, n ;

(4.6.3)

i 1

0 ,

1, m ,

1, n ,

(4.6.4)

где xij

- количество продукта, перевозимое из пункта Ai в пункт Bj ,

ai 0 ,

i 1, m и bj

0 ,

1, n . Любая допустимая точка задачи

может быть записана в виде матрицы

x11 ...

x1n

(xij )

... ... ... .

xm1

... xmn

Для приведения открытой задачи к закрытой необходимо

выполнить следующие действия:

1) если запасы больше потребностей:

bj ,

i 1

j 1

вводится фиктивый n+1 пункт назначения. Его

потребность bn

bj , а тарифы

Ci,n 1

1, m.

2) Если

, то вводится фиктивный (m+1)-й пункт

отправления, его запас am 1

Сm 1, j

1, m.

Рассмотрим два метода нахождения исходной базисной точки для транспортной задачи: метод "северо-западного угла" и метод минимального элемента.

4.6.1. Метод "северо-западного угла"

Алгоритм построения исходной базисной точки складывается из нескольких шагов, на каждом из которых

119

определяется верхний левый элемент матрицы X.
	1. Полагаем i			1	, j	0	1	,	a'		a ,	b'		b	j	, i	1, m , j	1, n .
			0			0			i		i	j			j
	2 Полагаем		x		min(a'			,b'		) . Если x						a' , то
			i0 j0				i0		j	0			i0 j0				i0
	переходим к шагу 3, в противном случае к шагу 5.
	3. Полагаем b'				b'		x	j0	. Индексу i					присваиваем
			j0		j0		i0	j0					0
	значение i0		1. Если i0					m , то переходим к шагу 4, в
	противном случае к шагу 2.
	4. Полагаем		x	j	b'	для всех					j	j	. Решение закончено.
			i0	j	j							0
	5. Полагаем		a'		a'		x	j0	. Индексу				j	присваиваем
			i0		i0		i0	j0					0
	значение	j0	1. Если				j0		n , то переходим к шагу 6, в
	противном случае переходим к шагу 2.
	6. Полагаем		x		a'	для всех i					i	. Решение закончено.
			ij0		i						0
	Рассмотрим пример использования данного алгоритма
Пример 1. Исходные данные:
bj	30		36				36						22				56
ai	30		36				36						22				56
ai
45	3				4						2					4		5
45	30		15
	30		15
70	3				1						4					2		4
70			21				36						13
			21				36						13
15	4				3						5					3		6
15													9				6
													9				6
50	2				4						3					6		8
50																	50
																	50
В	верхнем	правом				углу				в	каждой						ячейке	стоят
коэффициенты cij ,			i	1,4 ,		j 1,5 . Данная задача является закрытой
транспортной задачей, так как сумма потребностей в продукте равна
сумме имеющегося продукта
45+70+15+50=30+36+36+22+56.
							120

Результаты работы алгоритма записаны в нижнем левом углу ячейки. Получена исходная базисная точка

	30	15	0	0	0
X	0	21	36	13	0
X	0	0	0	9	6
	0	0	0	9	6
	0	0	0	0	50

со значением целевой функции, равным 804.

Метод "северо-западного угла" может оказаться очень "далеким" от оптимального, так как при построении начальной базисной точки этим методом мы совсем не реагируем на

коэффициенты целевой функции cij . Более близкие к оптимальным точки можно получить с помощью метода минимального элемента.

4.6.2.Алгоритм метода минимального элемента

1.Полагаем ai' ai , b'j bj , (i, j) , где

(i, j) : i 1, m, j 1, n .

Определяем пару индексов (i0 , j0 ) из условия

min cij ci0 j0 .

(i, j )

Полагаем x

min(a'

,b' ) . Если

, то переходим к

i0 j0

шагу 4, в противном случае - к шагу 7.

Полагаем b'

x .

i0 j

(i0 , j) : j 1, n .

Если множество

состоит из элементов одной строки ik , то

полагаем x

для всех (i , j)

. Решение закончено. В

ik j

противном случае переходим к шагу 2.

Полагаем a'

x .

i0 j0

(i, j0 ) : i 1, m .

Если множество

состоит из элементов одного столбца jk , то

полагаем x

для всех (i, j

)

. Решение закончено. В

ijk

противном случае переходим к шагу 2.

121

Данным методом найдем исходную базисную точку для примера 1.

Пример 2.

bj	30		36		36		22		56
ai	30		36		36		22		56
ai
45		3		4		2		4		5
45					36(2)				9(5)
					36(2)				9(5)
70		3		1		4		2		4
70			36(1)				22(3)		12(5)
			36(1)				22(3)		12(5)
15		4		3		5		3		6
15									15(5)
									15(5)
50		2		4		3		6		8
50	30(4)								20(5)
	30(4)								20(5)

Для наглядности каждый элемент снабжен индексом, равным номеру итерации, на которой был получен данный элемент. В результате получили следующую базисную точку

0 0 36 0 9

0 36 0 22 12

0 0 0 0 15

30 0 0 0 20

со значением целевой функции, равным 545. Данное значение явно меньше, чем значение целевой функции на базисной точке, полученной методом "северо-западного угла".

Замечание 1. Признаком вырожденности транспортной задачи является существование r m , s n , для которых выполняется равенство

r	s
a i	b j .
	k
k 1	l 1

В этом случае при использовании приведенных алгоритмов может оказаться, что среди n m 1 базисных координат есть нулевые.

122

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 1612 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20223.2 Mб13163.pdf
#
15.11.20223.21 Mб13165.pdf
#
15.11.20223.22 Mб13167.pdf
#
15.11.20223.22 Mб43168.pdf
#
15.11.20223.22 Mб33169.pdf
#
15.11.20223.23 Mб63172.pdf
#
15.11.20223.23 Mб13173.pdf
#
15.11.20223.23 Mб13174.pdf
#
15.11.20223.24 Mб23175.pdf
#
15.11.20223.25 Mб13177.pdf
#
15.11.20223.26 Mб03178.pdf