3172

В качестве критериев останова алгоритма применяются стандартные критерии:

143

Итерация 3

f (x2 ) ( 3, 3) .

Рассмотрим задачу

f (x2 )xT 3x1 3x2 min .

Решением этой ЗЛП является отрезок, соединяющий точки

(2,1) и (3,0) (рис.5.3.1).

Задачи для самостоятельного решения

Решить методом линеаризации следующие задачи:

146

ЗАКЛЮЧЕНИЕ

Знание математического аппарата, применяемого в инженерных исследованиях, умение пользоваться математическими моделями при оптимальном проектировании реальных объектов и систем с широким применением современных средств вычислительной техники должны позволить проектировщикам сложных систем и объектов ставить и решать задачи автоматизации проектирования в различных областях человеческой деятельности.

Изложенный в данном учебном пособии материал позволяет получить довольно полное представление о приемах математической постановки задач, их классификации и выборе методов решения. Подробные пояснения, сопровождающие поиск решения типовых задач, помогают легко справиться с заданиями, приведенными в каждом параграфе для самостоятельного решения. Ответы, которые можно найти в конце учебного пособия, дают возможность проверить правильность найденного решения.

Дополнительные теоретические сведения, а также задачи для самостоятельного решения можно получить из книг, приведенных в списке литературы.

147

ОТВЕТЫ

1.1.3.3; -24

1.1.4.1/0,61; -1/-0,61

1.1.6.4м×4м×2м

1.1.7.100м×150м

1.2.1.а) Umin (1;0) = -1; Umax = +

б) Zmin = 0, x* = 0, y* = 0; Zmax = 1e при х2 + y2 = 1

в) экстремумов нет

г) Zmax = 8e-2, х* = -4; y* = -2

д) экстремума нет

е) Zmin = 0, x* = 1, y* = - 12

ж) Zmin = 0, x* = 2, y* = 4 з) Zmin = 1, x* = -4, y* = 1

и) Zmax = 12, x* = y* = 4

1.2.3.Zmax = 5, x* = 1, y* = 2; Zmin = -5, x* = -1, y* = -2

1.2.4.fmax = 0,04; x* = 0,12; y* = 0,16; fmin = +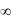

1.2.5.fmax = e1/4; x* = 0,5,; y* = 0,5; fmin = 0 не достигается

1.2.6.fmin = -25; x* = -0,5; y* = 1,5; fmax = +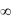

1.2.7.fmin = - ; Smax = +

148

1.2.8.a) fmin = - 2 /a; x* = -a/ 2 ; y* = -a/ 2 ; Smax = 2 /a; x* = a/ 2 ; y* = a/ 2

1.2.9.fmin = 9; x* = 3; y* = 3; fmax = +

fmin = 4 в точках (2,2,1), (2,1,2), (1,2,2)

1.2.13.fmin = e-1-1, x1* = 0; x2* = 0,5; fmin = e-1, x1* = 1; x2* = 0

1.2.14.fmin = 0, xi* = 0, i = 1, n ; fmax (±1,0,…,0) =…= Smax(0,…,0,±1) = 1

1.2.16.[d/ 3 ]3 или (d/ 3 )×( d/ 3 )×( d/ 3 )

1.2.17.(2R/ 3 )×(2R/ 3 )×(R/ 3 )

1.2.19.a = 4a · 4a · 4a · 4a

1.2.20.2a = 6, 2b = 2. Указание: x2+y2→extr; 5x2+8xy+5y2 = 9

1.2.21.Равнобедренный треугольник

1.2.22.L2(t) = t2-1/3

1.2.23.L3(t) = t3-3/5t

1.2.24.n1 , n1 ,..., n1

2.1.1.fmin = -1,1739, x* = 0,371

2.1.2.а) fmin = 1,910, x* = 1,038 б) fmin = 1,4653, x* = 0,6565

в) fmin = -22,5454, x* = 1,3713 г) fmin = -0,8385, x* = 0,6529 д) fmin = -8,9169, x* = 4

2.1.3.а) fmax = 1,1004, x* = 0,2016 б) fmax = 7,7290, x* = 2,3247 в) fmax = -0,0001, x* = -1,4916 г) fmax = 1,2524, x* = 0,5110 д) fmax = 3,6347, x* = -0,7549

149

е) fmax = 47,1449, x* = 3,3532

2.3.3.

1)fmin = 0; x* = (4; -3; -0,5);

2)fmin = 0; x* = (0,25; 0,75);

3)fmin = 0; x* = (1; 0);

4)fmin = 0; x* = (3; 2);

5)fmin = -1; x* = (1;1).

4.2.1.max=28, x1=6, x2=2.

4.2.2.max=14,8, x1=1,8, x2=2,8.

4.2.3.min=-4, x1=0, x2=2.

4.2.4.max=24, x1=6, x2=3.

4.2.5.max=2,67, x1=x2=0,67.

4.2.6.max=6,67, x1=x2=3,33.

4.2.7.max=7, x1=6, x2=1; min=3, x1=0, x2=3.

4.2.8.max=18, x1=3, x2=4.

4.2.9.max=14, x1=14, x2=0.

4.2.10.max=12, x1=4,8, x2=3,6.

4.3.1.min=7,1, x1=7,1, x2=x3=x5=0, x4=1,3, x6=0,4.

4.3.2.min=1,25, x1=0, x2=4,125, x3=0,25, x4=2,625.

4.3.3.min=0,75, x1=x2=0, x3=0,25.

4.3.4.max=24, x1=12, x2=0.

4.3.5.min=9,33, x1=1,33, x2=0,33.

4.3.6.min=-2,67, x1=0, x2=0,67.

4.3.7.max=210, x1=x2=17,5.

4.3.8.max=9, x1=3, x2=0.

4.3.9.max=67,21311, x1=10,16393, x2=x4=0, x3=2,95082.

4.3.10.min=1,25, x1=0, x2=4,125, x3=0,25, x4=2,625.

4.3.11.min=-4,5, x1=x2=0, x3=0,5, x4=1,5, x5=2.

4.3.12.max=10, x1=10, x2=x3=x4=0.

4.4.1.min=4, x1=5,11, x2=3,67, x3=x4=0, x5=2,56.

4.4.2.min=10, x1=1, x2=x3=x5=0, x4=7.

4.4.3.max=16,67, x1=0,67, x2=x5=0, x3=5,67, x4=4,67.

4.4.4.min=5, x1=1, x2=x4=0, x3=4, x5=7.

4.4.5.min=-2,375, x1=x4=0, x2=1,5, x3=0,625, x5=1,5.

4.4.6.max=7, x1=1, x2=x5=0, x3=4, x4=1.

4.4.7.min=1,25, x1=4,125, x2=0, x3=0,25, x4=2,625.

4.4.8.min=-2,33, x1=x4=x5=0, x2=1, x3=0,83, x6=2,167.

4.4.9.max=2, x1=x3=x4=x5=0, x2=1.

4.4.10.min=-2,4, x1=x4=x5=0, x2=5,6, x3=3,2.

150

4.5.1.min=10, x1=x2=1.

4.5.2.min=13, x1=2, x2=3.

4.5.3.max=-9, x1=1,5, x2=0.

4.5.4.min=9, x1=1,5, x2=0.

4.5.5.min=5, x1=0, x2=5.

4.5.6.min=15, x1=0, x2=1,5. 1

4.5.7.min=2, x1=x2=x4=0, x3=1, x5=3.

4.5.8.max=-30, x1=2, x2=0.

4.5.9.min=14, x1=7,33, x2=3,33.

4.5.10.min=159, x1=0,961538, x2=1,615385.

4.5.11.min=22,5, x1=4,5, x2=0.

151

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Акулич И. Л. Математическое программирование в примерах и задачах.-M: Высш. шк, 1986.-320 с.

2.Аттетков А.В., Галкин С.В., Зарубин В.С. Методы оптимизации: Учеб. для вузов. Под ред. В.С. Зарубина, А.П. Крищенко. – М.: Изд-во МПУ им. Баумана, 2001. – 440 с. (Сер. Математика в техническом университете; Вып. XIV)

3.Ашманов С.А. Линейное программирование. - M: Наука, 1981.-

304 с.

4.Ашманов С.А., Тимохов А.В. Теория оптимизации в задачах и упражнениях.- M.: Наука, 1991.- 448 с.

5.Банди Б. Основы линейного программирования. - M: Радио и связь, 1989.-176с.

6.Батищев Д.И., Шапошников Д.Е. Многокритериальный выбор с учетом индивидуальных предпочтений / ИПФ РАН. Н. Новгород,

1994. – 92 с.

7.Васильков Ю.В., Василькова Н.Н. Компьютерные технологии вычислений в математическом моделировании: Учеб. пособие. – М.: Финансы и статистика, 1999. – 256 с.: ил.

8.Гурия Л.С. Задачи и методы оптимального распределения ресурсов. – М.: Радио и связь, 1987. – 603 с.

9.Калихман И. Л. Сборник задач по математическому программированию.-M: Высш. шк, 1975.-261 с.

10.Курицкий Б.Я. Поиск оптимальных решений средствами Excel 7.0. – СПб.: ВHV – Санкт-Петербург, 1997. – 349 с.

11.Новиков Ф.А. Дискретная математика для программистов. – СПб.: Издательство “Питер”, 2001. – 304 с., ил.

12.Ногин В.Д., Протодьяконов И.О., Евлампиев И.И. Основы теории оптимизации.: Учеб. пособие для студентов втузов: - М.: Высш.

школа, 1986. – 384 с.

13.Таха Х. Введение в исследования операций. Т.1. – М.: Мир, 1985.

– 480 с.

14.Триус Е.Б. Задача математического программирования транспортного типа. – Киев: Вища школа, 1983. – 659 с.

15.Трифонов А.Г. Постановка задачи оптимизации и численные методы ее решения: Учебник. – М.: 2002. – 115 с.

16.Штойер Р. Многокритериальная оптимизация. Теория, вычисления и приложения: Пер. с англ. – М.: Радио и связь, 1992.

152