Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

3172

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

3.23 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 167 8 9 10 11 12 13 14 15 16 > Следующая >>>

d 2 (x*, y*) 0 ,

то точка x* является точкой минимума.

Ответ:	f	min	8,	x *	12, x *
		min		1	2
При	решении			большинства

задач проверка условия

(x* ), i

_____

линейной

независимости

векторов

1, m

затруднена,

так

как

точка

х*

заранее

неизвестна.

Однако это

требование

является существенным.

Пример 4. Найти условный экстремум в задаче

f0 (x)

min

f1 (x)

x13 x22

Решение.

1. Запишем функцию Лагранжа:

(x, y) x1 y1 (x13

x22 )

2. Выпишем необходимые условия экстремума :

а)

Ф(x, y)

3y x

Ф(x, y)

2 y1x2

б)

Ф(x, y)

x 3

Из второго равенства следует, что либо y1 =0, либо x2

0 .

При

первое

равенство

невозможно

(1=0),

значит

0. Но

из

третьего

равенства получаем

первое

равенство

снова

не выполняется

(1=0). В итоге

получаем, что

система несовместна и точек, подозрительных на экстремум, нет.

Однако,

проанализировав

исходную постановку

задачи,

нетрудно убедиться, что она разрешима. Из ограничения следует,


что	x	0 (так как x	( 3 x )2 ). Поэтому точка x*=(0,0) является
	1	1	2

решением данной задачи. Принцип Лагранжа не работает, потому

что в точке x* нарушено требование линейной независимости градиентов:

f1 (x*) ( 3(x1* )2 ,2x2* ) (0,0) .

Ответ: fmin 0, x1* x2* 0.

Чтобы избежать проверки линейной независимости градиентов в рассмотрение вводится так называемая расширенная функция Лагранжа:

~(x, y0 , y) y0 f0 (x) m yi (bi fi (x))

Те ор е м а 5 (расширенный принцип Лагранжа). Пусть х* -

точка	локального			экстремума		функции	f0 (x) ,	причем
		_____
fi (x), i		0, m	непрерывно дифференцируемы в окрестности точки
х.	Тогда		существует		такой	ненулевой		вектор
( y * , y* )		Rm 1, y*		( y * ,..., y * ), что для расширенной функции
0				1	m

Лагранжа

~(x, y0 , y) y0 f0 (x) m yi (bi fi (x))

выполняются следующие равенства:

1)	x	(x, y0 , y*) 0
2)	y	(x, y0 , y*) 0

В результате отыскание подозрительных на экстремум точек может осуществляться по следующему алгоритму:

Шаг 1. Составить расширенную функцию Лагранжа:

~ (x, y

, y)

(x)

(x))

Шаг 2. Записать необходимые условия экстремума:

1)	x	(x, y0	, y)	0
	x
2)	y	(x, y0	, y)	0
	y

Шаг 3. Решить систему для двух случаев:

1)y0=0;

2)y0=1.

Врезультате найти подозрительные на экстремум точки x*.

Возвратимся к примеру 4.

1. Составим расширенную функцию Лагранжа:

(x, y0 , y) y0 x1 y1 (x13 x22 )

2. Выпишем необходимые условия экстремума:

a)	(x, y)	y0	3 y1 x12 0,

	x1
	x1
	(x, y)	2 y1 x2		0,

	x2
	x2
b)	(x, y)	x13	x22	0

	y1
	y1

3. Положим y0=0.

Решая полученную систему, находим единственную точку (0,0). При y0=1, как мы уже выяснили, система несовместна.

Задачи для самостоятельного решения

3.1.1 Доказать, что всякая точка локального минимума в задаче выпуклого программирования является точкой глобального минимума.

3.1.2. Найти условный экстремум в задачах:

а) x 2	x 2	extr		б) x 2	x 2	extr
1	2			1	2
(x 1)2		x 2	4	x 2	x 2	1
1		2		1	2

3 . 1 . 3 . Д ок а з а т ь , ч т о ограничение вида fi (x) bi можно эквивалентно переписать как ограничение-равенство с помощью введения новой переменной ui :

fi (x) ui2 bi .

3.1.4. Получить необходимые условия экстремума для задач

а) f (x) extr	;	б) f0 (x)	extr
	;		,
x 0		f1 (x)	b

cведя их к задачам с ограничениями-равенствами.

3.2. Графическое решение задач нелинейного программирования

Если допустимое множество R , то задача оптимизации, как правило, может быть решена графически.

Определение. Кривые, задающиеся уравнениями

f (x1 , x2 ) C ,

называются линиями уровня функции f (x1, x2 ) .

Пример 1. Решить графически задачу нелинейного программирования

f (x , x )			(x	4)2 (x 2)2	min,
	1	2	1	2
x1	x2		3,		(1)
x1	2x2		4,		(2)

x1 , x2 0

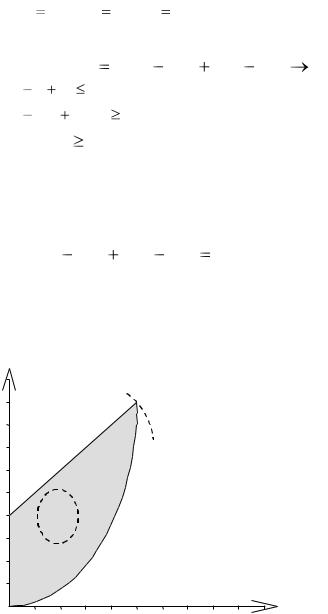
Решение: Допустимое множество задачи изображено на рис.3.2.1. Линиями уровня целевой функции являются концентрические окружности с центром в точке (4,2). Минимальному значению целевой функции соответствует окружность минимального радиуса, пересекающая допустимую область. Такая окружность будет касаться границы области на прямой (1). Дальнейшее уменьшение радиуса приводит к линиям уровня, не имеющим общих точек с областью.

Рисунок 3.2.1. Допустимое множество решений

Координаты точки касания можно найти, приравнивая значения производных (x2 )'x1 из уравнений прямой и окружности. Дифференцируя уравнение окружности

(x1	4)2 (x2			2)2		C,
и рассматривая x2 как неявную функцию от						x , получим
						1
'			2(x1	4)
(x2 ) x
(x2 ) x			2(x2	2) .
1			2(x2	2) .
1
Из уравнения прямой		находим (x )'			=1. В итоге выписывается
		2		x
				1

равенство:

12(x1 4)

2(x2 2) , т.е. x2 2 x1 4 .

Добавив уравнение прямой,		которой принадлежит точка касания,
получим систему:
x1	x2	3,
x2	x1	2 .

Ее решением является точка

X * ( 5 , 1 ) 2 2 .

Ответ: f		4.5; x *	5	;	x *	1	.
Ответ: f	min	4.5; x *		;	x *		.
	min	1	2		2	2
			2			2
Пример 2.

f (x1 , x2 )			2(x1 2)2 (x2 4)2	extr,
x1 x2	4,			(1)
9x 2	25x	2	0,	(2)
1	2
x1 , x2	0

Решение: Допустимое множество задачи изображено на рис.3.2.2. Линиями уровня целевой функции являются концентрические эллипсы с центром в точке (2,4) и задающиеся уравнением

2(x1 2)2 (x2 4)2 C .

Поскольку точка (2,4) принадлежит допустимому множеству, то она и будет являться точкой минимума задачи. Из графика видно, что максимальному значению функции соответствует эллипс, пересекающий границу области в точке

X max .

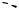
.Xmax

.Xmin

Рисунок 3.2.2.

Координаты этой точки находятся из условия пересечения

прямой и параболы:

9 x12

25x2

откуда

5, x2

max

43,

x *

Ответ:

0, x *

x *

min

Пример 3.

f (x1 , x2 )

extr

max{

}

2 .

Решение. Допустимое

множество

задачи

изображено на

рис.3.2.3. Линиями уровня целевой функции являются концентрические квадраты с центром в точке (2,0) и задающиеся уравнением

max{ x1 2 , x2 } C .

Минимальному значению целевой функции соответствует квадрат с минимальной стороной, пересекающий допустимую область.

1 .

1. x1

Рисунок 3.2.3

Из графика видно, что такой квадрат будет касаться границы допустимой области в двух точках. Координаты точек находятся из условий:

2 \| x1 \|	\| x2 \| 2
\| x1 2 \|	\| x2 \| .

Для той точки, которая лежит в первой четверти

0 x1 2, 0 x2 ,

поэтому система принимает вид:

2x1	x2	2
		,
2 x1		x2

откуда

x11 43 , x21 23 .

Вторая точка симметрична данной относительно оси Ох, поэтому ее координаты имеют вид

x11 43 , x21 23 .

При неограниченном увеличении стороны квадрата, линии уровня будут продолжать пересекать допустимую область, поэтому

sup f (x, y)

	Ответ:
X 1		4	,	2	, X 2	4	,	2	, sup f (x , x )	.
X 1			,		, X 2		,		, sup f (x , x )	.
min	3			3	min	3		3	1 2
	3			3		3		3

Пример 4.

f (x1, x2 ) (x1 5)x2 extr,

x12 x22 3

Решение: Допустимое множество задачи изображено на

рис.3.2.4. Линиями уровня целевой функции являются гиперболы с асимптотами x1 =5, x2 =0 и задающиеся уравнением

(x1 5)x2 C .

Минимум функции будет достигаться при С<0, максимум – при С>0. Обе точки являются точками касания окружности и гиперболы. Координаты точки касания находим, приравнивая

значения производных (x2 )'x1 нулю.

Рисунок 3.2.4

Дифференцируя уравнение гиперболы

(x1 5)x2 C ,

получим

(x2 ) x
(x2 ) x	x1	5 .
1	x1	5 .
1

Из уравнения окружности находим

					(x2 ) 'x									2x1
					(x2 ) 'x									2x2 .
										1				2x2 .
										1
В итоге выписывается равенство:
								x2				x1
						x				5		x	2		, т.е.		x 2						x 2		5x
								1					2		, т.е.	2							1		1 .
Добавив уравнение окружности, получим систему:
								x 2			x 2				5x ,
								2			1				1
								x 2			x 2				3	.
								1			2					.
С		учетом						условия x1							0 ,		ее решением являются точки

X min	(		1	,			11		),		X max				(		1		,				11	)
X min	(	2		,					),		X max				(	2			,					)
		2					2									2							2 .

						f					9.119, x *									1		,	x *		11	1.658;
						f		min			9.119, x *											,	x *			1.658;
								min							1	2							2		2
Ответ:																2									2
Ответ:
						f				9.119,					x *			1			,		x *		11	1.658.
						f		max		9.119,					x *						,		x *			1.658.
								max							1	2							2		2
																2									2

Задачи для самостоятельного решения

3.2.1. Решить графически задачи нелинейного программирования:

a) (x	1) 2	( y	1) 2	extr
(x	2)( y	1)	16,
x	0, y	0

<<< < Предыдущая 1 2 3 4 5 67 / 167 8 9 10 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20223.2 Mб13163.pdf
#
15.11.20223.21 Mб13165.pdf
#
15.11.20223.22 Mб13167.pdf
#
15.11.20223.22 Mб43168.pdf
#
15.11.20223.22 Mб33169.pdf
#
15.11.20223.23 Mб63172.pdf
#
15.11.20223.23 Mб13173.pdf
#
15.11.20223.23 Mб13174.pdf
#
15.11.20223.24 Mб23175.pdf
#
15.11.20223.25 Mб13177.pdf
#
15.11.20223.26 Mб03178.pdf

2 \| x1 \|	\| x2 \| 2
\| x1 2 \|	\| x2 \| .