
3172
.pdf
Теперь, когда нам известна исходная базисная точка, можно продолжить решение транспортной задачи методом потенциалов. Для этого построим задачу, двойственную к ТЗЛП:
m |
n |
|
aiui |
bj v j |
min |
i 1 |
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ui vj |
cij , i 1, m, j 1, n , |
|||||
|
ui , |
|
|
|
|
||||
где |
i 1, m |
- переменные двойственной задачи, |
|||||||
соответствующие ограничениям (4.6.2), a vj , j 1, n - переменные
двойственной задачи, отвечающие ограничениям (4.6.3). В соответствии с данным видом двойственной задачи, оценки в транспортной задаче будут иметь вид
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ij |
ui |
|
v j |
|
cij , i 1, m, j 1, n , |
|
|
|
|||||||||||||
причем переменные ui , i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1, m и vj |
, |
|
j |
1, n представляют собой |
||||||||||||||||||||
произвольное решение системы уравнений |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
ui |
vj |
cij , (i, j) |
|
|
B , |
|
|
|
|
|
|
|
(4.6.5) |
|||||||||
где B |
- множество базисных пар индексов. Заметим, |
что система |
||||||||||||||||||||||
(4.6.5) |
имеет |
n |
m |
переменных и |
|
m n 1 уравнение. Ранг |
||||||||||||||||||
системы равен m |
n |
1. Отсюда следует, |
что одну из переменных |
|||||||||||||||||||||
можно выбрать произвольно, например, |
u1 |
|
0 , а все остальные |
|||||||||||||||||||||
переменные найти по цепочке. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Сформулируем критерий оптимальности для транспортной |
|||||||||||||||||||||||
|
|
X |
|
(x0 ) , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
задачи. |
Пусть |
|
|
i |
1, m, j |
|
1, n |
- |
|
некоторое базисное |
||||||||||||||
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
решение транспортной задачи. |
B |
|
- множество базисных пар |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u0i , |
|
|
|
|
|
0 , j |
|
- |
|||||||||||||||
индексов данного базисного решения, |
|
i |
1, m и v j |
1, n |
||||||||||||||||||||
произвольное решение системы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
ui |
vj |
cij , (i, j) |
|
|
B . |
|
|
|
|
|
|
|
|
|
|
|||||||
Если существует пара индексов (i, j) |
|
|
|
B , для которой |
|
|
|
|||||||||||||||||
|
|
u |
0 |
v0 |
c , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
j |
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
то существует базисное решение X |
|
(xij ) , для которого |
|
|
|
|||||||||||||||||||
123

|
|
|
m |
|
|
|
m |
|
0 ; |
|
|
|
|
|
|
|
|
|
c x |
|
c x |
|
|
(4.5.6) |
|||
|
|
|
|
|
ij ij |
|
ij ij |
|
|
|
|
|
|
|
|
i 1 j |
1 |
|
i 1 j 1 |
|
|
|
|
|
|
||
если для всех пар индексов |
(i, j) |
B |
выполнено |
u0 |
v0 |
c |
, то |
||||||
|
|
|
|
|
|
|
|
|
i |
j |
ij |
|
|
X (x0 ) , |
|
|
|
|
|
|
|
|
|
|
|||
i 1, m, j |
1, n |
- решение |
задачи. Заметим, |
что |
для |
||||||||
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
транспортной задачи гарантируется построение новой базисной точки, так как эта задача при соблюдении баланса всегда разрешима. Отметим также, что неравенство (4.5.6) является нестрогим в связи с возможностью вырожденности базисных точек. Как следует из
алгоритма симплексного метода, если существует вектор Ai0 j0 с
положительной оценкой, то вектор Ai0 j0 должен быть введен в
базис. Для введения вектора в базис нужно знать его текущие координаты. В транспортной задаче для определения координат используется понятие цикла.
Определение. Говорят, что множество пар индексов (i, j) образует цикл, если их можно расположить, например, в следующей последовательности:
(i0 , j0 ) |
(i0 , j1 ) |
(i1, j1 ) |
... |
(ik , jk ) |
(ik , j0 ) |
(i0 , j0 ) |
Отметим, что каждые две рядом стоящие пары индексов должны иметь одинаковые номера строк или одинаковые номера столбцов. Сами пары, входящие в цикл, называются элементами цикла.
Пример цикла:
* |
* |
|
|
|
* |
|
* |
* |
|
* |
|
|
|
* |
* |
Цикл, который используется в алгоритме решения транспортной задачи, строится по следующему принципу:
ставятся (*) в клетках из множества B и в клетке (i0 , j0 ) , которая
будет вводиться в базис. Просматриваются все строки таблицы и вычеркиваются те строки, в которых имеется не более одной (*). Затем вычеркиваем те столбцы, в которых содержится не более одного элемента. Затем снова просматриваются строки и т.д.
124

Оставшиеся элементы образуют цикл.
Когда цикл построен, можно следующим образом найти коэффициенты вводимого вектора: перенумеровать все элементы цикла, присвоив вводимому элементу 0, следующему 1 и т.д.;
коэффициенты разложения вектора Ai0 j0 равны +1 по векторам из
цикла с нечетными номерами, -1 - по элементам цикла с четными номерами и 0 по векторам, не входящим в цикл. Обозначим через
 множество индексов (i, j) с четными номерами, через
множество индексов (i, j) с четными номерами, через  - множество индексов (i, j) с нечетными номерами .
- множество индексов (i, j) с нечетными номерами .
Зная координаты вектора Ai0 j0 , его можно ввести в базис по правилам симплексного метода. Поскольку координаты вводимого
вектора равны +1 или -1, то значение |
min x0 |
x0* * . Вектор с |
|||
|
|
(i, j ) |
ij |
i |
j |
|
|
|
|||
|
|
|
|
|
|
(i* , j* ) |
B , на котором достигается |
этот минимум, |
считается в |
||
дальнейшем небазисным. Остальные базисные координаты новой базисной точки пересчитываются по формулам:
|
|
xH |
x0 |
, (i, j) |
|
, |
|||
|
|
ij |
ij |
|
|
|
|
|
|
|
|
xH |
x0 |
, (i, j) |
|
, |
|||
|
|
ij |
ij |
|
|
|
|
|
|
где xH |
x |
по элементам, не входящим в цикл. Вычисление нового |
|||||||
ij |
ij |
|
|
|
|
|
|
|
|
значения функции цели может быть произведено по формуле |
|||||||||
|
|
LH |
L |
i |
0 |
j |
. |
|
|
|
|
|
|
|
|
0 |
|
|
|
Может |
оказаться, что |
|
min x0 |
достигается в нескольких |
|||||
|
|
|
|
(i, j ) |
ij |
|
|||
|
|
|
|
|
|
||||
нечетных элементах цикла. Тогда небазисным для новой базисной точки считается только один из них, например, тот, которому соответствует наибольшее значение функции цели. Остальные элементы считаются базисными со значением в новой базисной точке, равными нулю. В этом случае мы имеем вырожденную базисную точку.
4.6.3. Алгоритм метода потенциалов
Итерация 0.
0.1.Определить исходная базисная точка с помощью любого из алгоритмов построения начального базиса.
125

0.2. Вычислить значение целевой функции
z(x0 ) |
|
c x0 |
, |
B |
|
|
ij ij |
|
|
|
(i, j ) |
B |
|
|
- множество базисных индексов.
0.3.Положить k 0 .
Итерация k 1.
Пусть на k -той итерации получена базисная точка xk со значением целевой функции z(xk ) .
k+1. 1. Положить u1 |
0 и определить vj cij |
u1 , (i, j) |
B . |
|||||||||||
Если некоторое vs вычислено, то определить |
|
|||||||||||||
ui |
|
cis vs |
, |
|
|
|
|
|
|
|
||||
(i, s) |
. |
|
и т.д., пока не будут вычислены все ui |
, |
||||||||||
|
|
|
|
|
|
|
|
|
||||||
i 1, m и vj , |
j 1, n . |
|
|
|
||||||||||
k+1. 2. Вычисляют оценки небазисных векторов |
|
|
||||||||||||
ij |
|
|
ui |
vj |
|
cij . |
|
|
|
|
||||
k+1. 3. Выбрать |
i |
0 |
j |
0 |
max |
ij . |
|
|
|
|||||
|
|
|
|
|
|
|
i, j |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k+1. 4. Если |
i0 j0 |
|
|
0 , то СТОП, |
xk - решение задачи. |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k+1. 5. По правилу вычеркивания определить цикл, |
|
|||||||||||||
образованный парой (i0 , j0 ) вместе с базисными парами |
||||||||||||||
индексов. |
|
|
|
|
|
|
|
|
|
|
||||
Пусть |
- множество четных элементов цикла, |
- |
|
|||||||||||
множество нечетных элементов цикла без (i0 , j0 ) . |
|
|||||||||||||
k+1. 6. Определить |
|
|
min |
xk |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
(i, j ) |
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
k+1. 7. Положить |
|
|
|
|
xk |
1 |
, |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
i0 j0 |
|
|
|
|
xk 1 |
xk |
|
|
|
|
, (i, j) |
|
|
|
|
||||
ij |
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
xk 1 |
|
xk |
|
|
|
|
, (i, j) |
|
|
|
|
|||
ij |
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
126

k+1. |
8. |
Определить ci j |
|
|
max |
cij и элемент ci j |
считать |
|||
|
|
l |
l |
(i, j ) , xij |
0 |
|
|
l |
l |
|
|
|
|
|
|
|
|
|
|||
|
|
небазисным. |
|
|
|
|
|
|
|
|
k+1. |
9. |
Вычислить z(xk 1 ) |
z(xk ) |
i |
|
j |
. |
|
||
|
|
|
|
|
|
0 |
0 |
|
||
|
|
|
|
|
|
|
|
|
||
k+1. |
10. Положить k |
|
k |
1. |
|
|
|
|
|
|
Пример. 3
Итерация 0. Определяем начальный базис методом минимального элемента.:
bj |
12 |
|
8 |
|
7 |
|
7 |
|
6 |
|
ai |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
6 |
|
7 |
|
4 |
|
3 |
|
2 |
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
3 |
|
4 |
|
3 |
|
5 |
|
1 |
0 |
|
|
|
2 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|||
12 |
|
0 |
|
4 |
|
2 |
|
3 |
|
6 |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
7 |
|
1 |
|
8 |
|
4 |
|
5 |
|
|
8 |
|
5 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
L(x0 ) 0*12+1*8 +1*6 + 2*6 + 3* 0 + 3*2 + 8* 5 + 4*1 = 76
 {(1,4), (2,1), (2,3), (2,5), (3,1), (4,2), (4,3), (4,4)}
{(1,4), (2,1), (2,3), (2,5), (3,1), (4,2), (4,3), (4,4)}
Итерация 1.
1.1Помечаем звездочками места, занимаемые базисными элементами. Полагаем u1 0 .
v4 |
c14 |
u1 |
2 |
u4 |
c44 |
v4 |
2 |
v2 |
c42 |
u4 |
1 |
|
v3 |
c43 |
u4 |
6 u2 |
c23 |
v3 |
3 |
v1 |
c21 |
u2 |
6 |
||
v1 |
c21 |
u2 |
6 |
v5 |
c25 |
u2 |
4 |
u3 |
c31 |
v1 |
6 |
|
1.2 Оценки |
ij |
записываем на свободные места таблицы: |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
127

vj |
6 |
-1 |
6 |
|
2 |
4 |
ui |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
-1 |
-5 |
|
3 |
* |
-1 |
|
|
|
|
|
|
|
-3 |
* |
-8 |
* |
|
-6 |
* |
-6 |
* |
-11 |
-2 |
|
-7 |
-8 |
2 |
-3 |
* |
* |
|
* |
1 |
1.3(i0 , j0 ) (1,3) .
1.413 3 0 .
1.5Отмечаем звездочкой элемент (1,3) и по правилу вычеркивания определяем цикл.
|
|
|
|
|
|
|
|
|
* |
|
* |
|
|
|
|
* |
|
|
|
|
|
|
|
|
* |
|
|
|
|
* |
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
* |
|
* |
|
|
|
|
|
Цикл образуют элементы (1,3) |
(1,4) |
(4,4) |
(4,3) . |
|
||||||||||
|
|
{(4,4)} , |
|
{(1,4),(4,3)} . |
|
|
|
|
|
|
|||||
1.6 |
|
min(6,5) |
|
5 . |
|
|
|
|
|
|
|
|
|
||
1.7 |
x130 |
|
|
5 , x141 |
6 |
5 |
|
1 , x143 |
5 5 |
0 , x144 |
5 1 6 , |
|
|||
|
|
x210 |
0 , x123 |
2 , x125 |
6 , x311 |
12 , x142 8 . |
|
|
|
||||||
1.8 Имеется только один элемент (4,3) из |
, для которого x0 |
0 . |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
43 |
|
|
|
Поэтому он становится небазисным. Новая базисная точка имеет |
||||||||||||||
|
вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
5 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
x1 |
0 |
0 |
2 |
0 |
6 . |
|
|
|
|
|
|
|
||
|
|
12 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
0 |
8 |
0 |
6 |
0 |
|
|
|
|
|
|
|
|
|
1.9 L(x1) |
L(x0 ) |
x131 |
13 |
|
76 5*3 |
61 |
|
|
|
|
|||||
Итерация 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
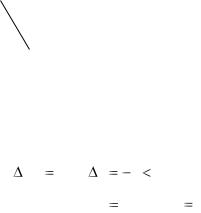
2.1, 2.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
128
vj |
3 |
-1 |
3 |
2 |
1 |
|
ui |
||||||
|
|
|
|
|
||
|
|
|
|
|
|
|
0 |
-4 |
-5 |
* |
* |
-4 |
|
|
|
|
|
|
|
|
0 |
* |
-5 |
* |
-3 |
* |
|
|
|
|
|
|
|
|
-3 |
* |
-8 |
-2 |
-4 |
-8 |
|
|
|
|
|
|
|
|
2 |
-2 |
* |
-3 |
* |
-2 |
|
|
|
|
|
|
|
2.3, 2.4. |
i0 |
max |
ij |
2 |
0 . |
|
j0 |
|
|
||
Решение закончено. |
x* x1 , |
L(x* ) 61. |
|||
Задачи для самостоятельного решения
Решить следующие задачи методами потенциалов, минимального элемента и “северо – западного угла”:
4.6.1 |
a\b |
25 |
40 |
50 |
35 |
45 |
|
20 |
7 |
3 |
4 |
8 |
6 |
|
60 |
5 |
7 |
2 |
3 |
5 |
|
45 |
1 |
4 |
5 |
2 |
6 |
|
70 |
3 |
4 |
2 |
7 |
8 |
|
|
|
|
|
|
|
4.6.2 |
a\b |
35 |
30 |
50 |
25 |
|
|
50 |
8 |
6 |
7 |
3 |
|
|
50 |
7 |
4 |
9 |
3 |
|
|
55 |
6 |
1 |
4 |
5 |
|
|
50 |
7 |
8 |
3 |
4 |
|
|
|
|
|
|
|
|
4.6.3 |
a\b |
10 |
40 |
20 |
60 |
20 |
|
30 |
5 |
1 |
5 |
2 |
4 |
|
70 |
5 |
7 |
6 |
3 |
2 |
|
25 |
1 |
5 |
4 |
2 |
6 |
|
25 |
1 |
6 |
3 |
3 |
5 |
129
4.6.4 |
a\b |
70 |
40 |
30 |
60 |
50 |
|
20 |
6 |
1 |
7 |
3 |
3 |
|
90 |
7 |
4 |
4 |
8 |
4 |
|
80 |
8 |
2 |
3 |
5 |
7 |
|
60 |
3 |
4 |
2 |
8 |
5 |
4.6.5 |
a\b |
30 |
90 |
80 |
20 |
30 |
|
95 |
2 |
8 |
4 |
6 |
3 |
|
55 |
3 |
2 |
5 |
2 |
6 |
|
40 |
6 |
5 |
8 |
7 |
4 |
|
60 |
3 |
4 |
4 |
2 |
1 |
|
|
|
|
|
|
|
4.6.6 |
a\b |
10 |
30 |
25 |
15 |
20 |
|
20 |
9 |
1 |
5 |
7 |
1 |
|
15 |
2 |
8 |
4 |
8 |
1 |
|
45 |
2 |
3 |
2 |
8 |
5 |
|
20 |
6 |
1 |
3 |
4 |
7 |
|
|
|
|
|
|
|
4.6.7 |
a\b |
13 |
13 |
13 |
13 |
28 |
|
28 |
8 |
4 |
6 |
3 |
1 |
|
13 |
9 |
3 |
8 |
5 |
7 |
|
19 |
7 |
3 |
5 |
9 |
8 |
|
20 |
2 |
1 |
4 |
5 |
7 |
|
|
|
|
|
|
|
4.6.8 |
a\b |
11 |
13 |
26 |
10 |
10 |
|
24 |
9 |
1 |
3 |
2 |
7 |
|
12 |
6 |
9 |
4 |
1 |
5 |
|
18 |
9 |
1 |
2 |
8 |
5 |
|
16 |
3 |
3 |
9 |
6 |
8 |
|
|
|
|
|
|
|
4.6.9 |
a\b |
10 |
35 |
15 |
25 |
35 |
|
30 |
7 |
3 |
1 |
5 |
4 |
|
25 |
7 |
5 |
8 |
3 |
2 |
|
45 |
6 |
4 |
8 |
3 |
2 |
|
20 |
3 |
1 |
7 |
6 |
2 |
130

4.6.10 |
a\b |
30 |
80 |
65 |
35 |
40 |
|
60 |
8 |
2 |
4 |
9 |
1 |
|
55 |
7 |
5 |
5 |
3 |
6 |
|
85 |
9 |
4 |
6 |
2 |
7 |
|
50 |
5 |
3 |
2 |
6 |
4 |
5. ЗАДАЧА КВАДРАТИЧНОГО ПРОГРАММИРОВАНИЯ
5.1.1. Постановка задачи квадратичного программирования
Задачей квадратичного программирования называется задача выпуклого программирования минимизации квадратичной
функции на допустимом множестве |
, заданном линейными |
ограничениями |
|
xT Qx bxT c min x ,
где Q (qij ) - симметричная положительно определенная матрица
размера n n , b - фиксированный вектор размера n , с - заданное число.
Рассмотрим задачу квадратичного программирования вида:
|
n |
|
|
|
_____ |
|
|
gi (x) |
|
|
|
ij x j |
i |
0, i=1,m , |
(5.1.1) |
|
j 1 |
|
|
|
|
|
|
|
1 |
|
n |
n |
|
n |
|
f (x) |
|
|
|
qij x j |
bj x j c |
min , |
|
2 i |
|
||||||
|
1 |
j 1 |
|
j 1 |
|
||
|
|
|
|
____ |
|
|
|
xj 0, j=1,n . |
|
|
|
||||
Для данной задачи условной оптимизации можно |
|||||||
рассмотреть функцию Лагранжа вида: |
|
||||||
|
|
|
|
|
n |
n |
|
L(x, , ) |
|
f (x) |
|
i gi (x) |
j ( x j ) |
||
|
|
|
|
|
i 1 |
j 1 |
|
|
|
|
|
131 |
|
|
|

1 n |
n |
n |
|
||
|
|
|
qij x j |
bj x j |
c |
2 i 1 |
|
||||
j |
1 |
j 1 |
|
||
n |
|
n |
|
n |
|
|
i ( |
|
ij x j |
i ) |
i ( x j ) . |
i 1 |
j |
1 |
j |
1 |
|
При этом условия Куна - Таккера запишутся в виде следующей системы равенств и неравенств:
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
x j |
0, |
|
j |
1, n |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
j |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
L |
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
q ij x i |
b j |
|
|
i |
ij |
|
|
j |
|
0, j 1, n |
|||||||||||||||
x j |
|
|
|
|
|
|||||||||||||||||||||
i 1 |
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
L |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
ij x j |
|
|
|
i |
0, i |
1, m |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
i |
|
|
|
j 1 |
|
|
|
|
|
|
|
|
|
|
(5.1.2) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i gi |
i |
|
|
ij x j |
i |
0, i 1, m |
||||||||||||||||||
|
|
|
|
|
|
|
j |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
j x j |
0, |
|
|
j |
|
1, n |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
i |
0, |
i |
1, m, |
|
|
j |
0, |
|
j 1, n. |
|||||||||||||||
5.1.2. Использование симплексного метода для решения задачи квадратичного программирования
По теореме Куна - Таккера решение системы (5.1.2) является
искомой точкой минимума функции |
f (x) |
(5.1.1) на множестве . |
|||||
|
|
|
|
|
_____ |
|
|
Введя дополнительные |
переменные |
xn |
1 , i=1,m, полученную |
||||
систему перепишем в виде системы равенств |
|||||||
n q ij x j |
n |
|
|
|
|
|
|
i |
ij |
j |
b j , j 1, n |
||||
i 1 |
i 1 |
|
|
|
|
|
|
132
