1784

Список литературы приводится в конце КР. Ссылка в тексте на литературный источник указывается порядковым номером по перечню литературы, выделенным двумя квадратными скобками (например [3]). В перечень литературы, составленный в порядке упоминания в тексте, включают только те источники, на которые имеются ссылки в тексте. Не допускается ставить ссылки на источники, использованные в заголовках разделов или подразделов.

Сведения о книгах (учебниках, справочниках и т. п.) должны включать: фамилию (фамилии) и инициалы автора (авторов), полное название книг, место издания, издательство, год издания и количество страниц.

Листы КР должны быть сброшюрованы в тетрадь. Выполненная КР после ее проверки руководителем

должна быть защищена в установленный им срок. Защита КР является формой проверки выполнения работы, она должна научить студента всестороннему обоснованию выполненного решения и прояснить глубину понимания им выполненной работы.

Защита КР проводится в форме собеседования со студентом по вопросам работы и решения студентом типовых задач на тему КР. Студент должен дать все необходимые объяснения по существу КР и решить предложенные ему задачи.

Задаваемые вопросы должны соответствовать теме КР и относиться к выяснению сущности и особенностей, применяемых в КР методов расчета, области их приложения, анализу полученных результатов. При необходимости более глубокой проверки знаний студента ему могут быть заданы вопросы по теоретическому курсу, связанные с содержанием КР.

Вариант задания на курсовую работу выбирается студентом в соответствии с его номером в журнале группы. Задание выдается на установочной лекции или на ежемесячных консультациях.

50

2.2. Основные понятия и зависимости [1]

При прямом изгибе балки ее ось, искривляясь, остается в силовой плоскости. Изогнутая ось балки, представляющая собой геометрическое место центров тяжести поперечных сечений деформированной балки, называется упругой линией. Деформация балки в плоскости yz характеризуется двумя перемещениями (рис. 2.2):

y Θ

y z

Θ

Рис. 2.2

1)прогибом (y) – линейным перемещением точек оси балки по нормали к ее первоначально прямой оси;

2)углом поворота сечения (Θ) – углом, на который поворачивается поперечное сечение балки относительно его первоначального положения (поперечное сечение остается плоским и перпендикулярным изогнутой оси балки).

2.2.1. Определение перемещений методом Мора. Порядок расчета

Метод Мора представляет собой универсальный метод определения линейных и угловых перемещений. Для того чтобы определить методом Мора перемещение i (прогиб или угол поворота) в некотором сечении бруса, необходимо:

54

1)рассмотреть «грузовое» состояние (“Р”), представляющее балку под действием заданных нагрузок;

2)рассмотреть «единичное» состояние (“i”), представляющее ту же балку, освобожденную от заданных нагрузок и нагруженную единичным силовым фактором (единичной силой, когда определяется прогиб, или единичным моментом, когда определяется угол поворота), приложенным в сечении, перемещение которого определяется, в направлении искомого перемещения;

3)«грузовое» и «единичное» состояния разбить на одинаковые участки;

4)на каждом k - м участке записать аналитические выражения изгибающих моментов, соответствующих «грузово-

му» состоянию Mxp(k) и «единичному» состоянию Mxi(k) ;

5) определить искомое перемещение, как сумму интегралов Мора по участкам балки

где m – число участков; k – номер участка; lk – длина участка;

EIx k – изгибная жесткость участка.

Если i > 0, то направление искомого перемещения совпадает с направлением единичного силового фактора, если

i < 0, то противоположно ему.

2.2.2.Определение перемещений способом Верещагина. Порядок расчета

Если стержневая система состоит из прямолинейных участков с постоянной в пределах каждого из них жесткостью, то интегралы Мора можно вычислять по способу Верещагина.

55

Определение способом Верещагина перемещения i

(прогиба или угла поворота) некоторого сечения балки ведут в следующей последовательности:

1) строят независимо друг от друга эпюру изгибающих моментов Mxp для «грузового» состояния и эпюру изгибаю-

щих моментов Mxi для «единичного» состояния, соответст-

вующего искомому перемещению;

2)обе эти эпюры разбивают на одинаковые участки, в пределах каждого из которых эпюра изгибающих моментов «единичного» состояния является регулярной функцией (непрерывной и не имеющей точек излома), а изгибная жесткость бруса постоянна;

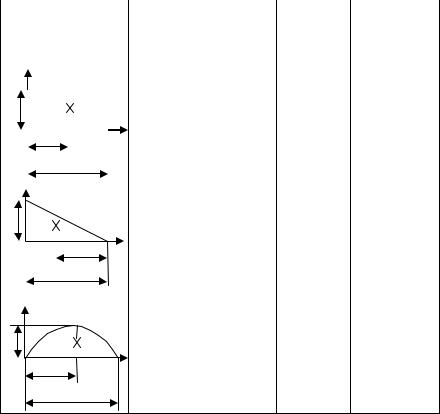
3)площадь эпюры изгибающих моментов «грузового» состояния разбивают на простые площади. При этом можно ограничиться тремя вариантами простых площадей – прямоугольник, прямоугольный треугольник и параболический сег-

мент. Далее определяют площадь k каждой простой фигуры

и показывают положение ее центра тяжести. Значения площадей и положения их центров тяжести для перечисленных простых фигур приведены в табл. 2.2;

4)под центром тяжести каждой площади ωk определяют ординату Mki на эпюре изгибающих моментов “единичного” состояния;

5)искомое перемещение определяют по формуле

где k – номер площади; m – число простых фигур, на которые разбита эпюра изгибающих моментов “грузового” состояния. Произведение ωkMki считается положительным, если часть эпюры изгибающих моментов “грузового” состояния, имеющая площадь ωk, и соответствующая ей ордината Mki расположены по одну сторону от нулевой линии.

56

Положительное значение перемещения δi получается в случае, если его направление совпадает с направлением единичного силового фактора (единичных силы или момента).

b

Заметим, что если интенсивность q распределённой нагрузки, действующей на балку, постоянна или распределённая нагрузка отсутствует, то эпюру Mxp “грузового” состояния всегда можно разбить на площади, представленные в табл. 2.2. Для доказательства рассмотрим, например, балку, изображённую на рис. 2.3, а, эпюра изгибающих моментов которой пред-

57

ставлена на рис. 2.3, б. Тогда выражение для изгибающего момента Mxp можно записать в виде

При этом высота h параболического сегмента (табл. 2.2) в случае равномерно распределённой нагрузки интенсивностью

q всегда равна qb2 . Таким образом, площадь ω эпюры изги- 8

бающего момента Mxp равна 1 2 3 (площадь 3 параболического сегмента отрицательна, если распределённая нагрузка направлена вверх (рис. 2.3, д) и положительна, если распределённая нагрузка направлена вниз).

2.2.3. Расчет на жесткость при изгибе

Расчет на жесткость при изгибе балок выполняют исходя из условий жесткости [3]:

ymax y ,max ,

58