
1499
.pdf
менив теорему Остроградского – Гаусса для вектора напряженности через цилиндр с радиусом r, расположенный коаксиально пучку, и уравнение (1.6), получим для радиальной силы выражение
|
|
|
|
|
|
|
|
Fre |
= −eEr |
= |
|
|
|
eI0 r |
|
|
|
|
. |
|
(1.11) |
|||
|
|
|
|
|
|
|
|
2π r02ε 0 |
2e |
Ua |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
||||
|
|
|
Здесь r0 – радиус пучка (определяется граничными траек- |
|||||||||||||||||||||
ториями). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Дифференцируя по |
z уравнение |
|
(1.10), |
используя |
|||||||||||||||||
|
d |
= |
dz |
|
d |
, |
dz |
= Vz |
и подставляя Fre, |
находим уравнение гра- |
||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
dt dt dz |
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ничной траектории: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
d 2 r |
= |
|
|
|
I |
0 |
|
|
|
= |
|
p |
|
|
||
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
. |
(1.12) |
||||
|
|
|
|
|
|
|
|
dz2 |
|
|
|
2e 1/ 2 |
3/ 2 |
|
kr0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
4πε 0 r0 |
|
|
|
Ua |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
||
Мы снова видим важность первеанса как характеристики пространственного заряда. Здесь k = 6,6·10–4 A/В–3/2 . Если расширение пучка ограничено величиной ∆ = r – r 0, которая мала в сравнении с r0, тогда r0 в правой части уравнения (1.12) может быть принято постоянным, после интегрирования получим следующее уравнение:
r0 |
= amin |
+ |
1 |
|
p |
z2 , |
(1.13) |
|
|
||||||
|
|
|
2 kamin |
|
|||
гдеamin – минимальныйдиаметрпучка. Еслипервеансp = 10–8 |
A/В–3/2 , |
||||||
то расширение ∆ не превышает 1 % от длины z пучка, если радиус пучка не превосходит 0,77 мм.
Более точное решение уравнения (1.13) предложено Глазером. Оно дает универсальное соотношение между безразмер-
ным радиусом r0/amin и параметром Z =174 z p  amin . Это соотношение показано на рис. 1.6.
amin . Это соотношение показано на рис. 1.6.
31
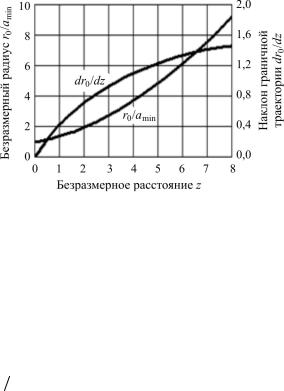
Рис. 1.6. Универсальное соотношение между безразмерным расстоянием, безразмерным радиусом и наклоном граничной траектории
Здесь amin определено как
|
= amin |
kα |
02 |
|
||
az0 |
exp |
|
|
, |
||
2 p |
||||||
|
|
|
|
|||
где |
α0 |
– |
начальный угол сходимости граничной траектории, |
α 0= |
( – |
dr0 |
dz )z = z0; az0 – начальный радиус пучка. Когда имеем |
расширяющийся пучок, α 0 отрицательно.
1.1.6. Компенсация пространственного заряда электронного пучка ионами. Магнитная и ионная самофокусировка интенсивного электронного пучка
Кроме собственного электрического поля движущиеся электроны создают также магнитное поле. В соответствии с законом Био-Савара – Лапласа магнитную индукцию B вблизи поверхности цилиндрического пучка радиусом r0 можно определить как
B = − µ0 I0 , 2π r0
32

а радиальную силу, действующую на граничные электроны в сторону оси пучка, как
Frm |
= − |
eµ0 I0 |
. |
(1.14) |
|
||||
|
|
2πr0 |
|
|
Суммарная радиальная сила, действующая в результате взаимного отталкивания электронов и магнитного притягивания, находится суммированием уравнений (1.11) и (1.14):
FrΣ = |
eI |
0 |
|
1 |
− µ |
|
|
|
|
|
|
0Vz . |
(1.15) |
||||
2πr0 |
ε0Vz |
|||||||
|
|
|
|
|
||||
Имея в виду, что ε0 и µ0 связаны соотношением
ε0µ0 = 12 ,
C
уравнение (1.15) можно переписать:
|
= |
eI |
0 |
|
− |
V |
2 |
|
FrΣ |
|
1 |
z |
. |
||||
|
|
2 |
||||||
|
|
2πε0Vz r0 |
|
C |
|
|
||
Если V << C, магнитная радиальная сила пренебрежимо мала, поэтому действие собственного магнитного поля следует учитывать только для релятивистских электронов.
В случае частичной компенсации пространственного заряда пучка положительными ионами, генерированными электронным пучком или внесенными извне, относительный пространственный заряд компенсирующих ионов можно записать как f:
f = ρions .
ρelectrons
Тогда общая радиальная сила, действующая на граничный электрон,
|
d 2 r |
= |
|
|
I0 |
|
|
|
|
− f − |
V 2 |
|
|||
m |
|
|
|
|
|
|
|
|
|
1 |
|
|
, |
||
dt |
2 |
|
|
1/ 2 |
|
|
|
C |
2 |
||||||
|
|
|
4πε |
e |
|
3/ 2 |
|
|
|
|
|
||||
|
|
|
|
0 m 2 |
|
|
U |
0 |
r0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
33

и, соответственно, траектория граничного электрона
d 2 r |
= |
|
|
I0 |
|
|
|
|
− f − |
V 2 |
|
|||
|
|
|
|
|
|
|
|
|
1 |
|
|
. |
||
dz |
2 |
|
|
1/ 2 |
|
|
|
C |
2 |
|||||
|
|
4πε |
e |
|
3/ 2 |
|
|
|
|
|
||||
|
|
|
0 m 2 |
|
|
U |
0 |
r0 |
|
|
|
|
||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
Когда f < 1, требуется учет влияния частичной компенсации заряда ионами, при f > 1 (перекомпенсированный пространственный заряд) наблюдается эффект ионной самофокусировки пучка положительными ионами, находящимися в объеме пучка. В случае f = 1 (полная компенсация) имеет место магнитная самофокусировка пучка, которая является результатом комбинированного воздействия ионной компенсации и магнитного пинч-эффекта.
Радиальное распределение потенциала U (r) для идеального случая пучка с равномерным пространственным зарядом показано на рис. 1.7, а, случаи реального электронного пучка с нормальным распределением плотности тока – на рис. 1.7, б.
Рис. 1.7. Распределение потенциала в радиальном направлении в поперечном сечении электронного пучка: а– равномерное распределение; б– Гауссово распределение плотности тока пучка; 1 – интенсивный электронный пучок в высоком вакууме; 2 – частичная компенсация пространственного заряда; 3 – перекомпенсация отрицательного пространственного заряда
генерированными ионами
34

1.1.7. Общее влияние эмиттанса, пространственного заряда электронов и его ионной нейтрализации на конфигурацию пучка
Пусть пучок проходит через очень маленькое поперечное сечение в пространстве в отсутствие внешних электрических и магнитных полей (рис. 1.8). Примем, что влияние пространственного заряда электронов и находящихся в нем ионов, как и их магнитного поля, пренебрежимо мало. В результате траектории отдельных электронов являются прямыми линиями. Луч – неламинарный, т.е. эмиттанс ε ≠ 0. Некоторые типичные траектории показаны на диаграммах эмиттанса в фазовой плоскости rr' для некоторых поперечных сечений. Известно, что точки, лежащие на эллипсе в одном поперечном сечении I, лежат на эллипсах с такими же площадями в остальных поперечных сечениях (II, III и IV) в таком же порядке. Ориентация осей эллипса соответствует сходящемуся или расходящемуся пучку, как это видно по траекториям пучка, показанным на рис. 1.8. Для практических целей важны граничные траектории (очерченные пунктирными линиями). Уравнение этих траекторий – уравнение гиперболы с полушириной amin и асимптотическим углом ε /amin:
d 2 a − ε 2 = 1 . dz2 a3
С учетом равномерного распределения по длине поперечного сечения пучка пространственного заряда электронов и частично компенсирующих ионов, захваченных в потенциальном минимуме в пространстве пучка и в присутствии аксиально-сим- метричного электрического поля, уравнение одного параксиального граничного электрона принимает вид
|
U ' |
|
U '' |
ε2 |
|
(1 − f −Vz2 C 2 )I0 m1/ 2 |
1 |
|
|||
a ''+ a |
' |
− |
|
a − |
|
− |
|
|
|
|
= 0 (1.16) |
|
a3 |
4 2πε |
|
|
|||||||
|
2U 4U |
|
0U 3/ 2e1/ 2 |
a |
|
||||||
35

Рис. 1.8. Траектории и диаграммы эмиттанса в неламинарном пучке, проходящем в пространстве, в отсутствие внешних электрических и магнитных полей
Здесь индексы «'» и «''» обозначают операторыd dz и d 2
dz и d 2  dz2 . Первый и последний члены формируют уравнение
dz2 . Первый и последний члены формируют уравнение
расходящегося пучка в свободном от поля пространстве. Если a' и a''равны 0, формулируется закон Чайлда – Ленгмюра (1.8) при потенциале U~Z4/3.
Для определения эмиттанс или пространственный заряд преобладает как фактор, управляющий поведением пучка с радиусом a, 4-й и 5-й члены в уравнении (1.16) сравниваются:
|
m |
|
|
|
|
1 − f |
− Vz |
pa2 ≥ ε 2 . |
||
|
|
|
|
|
||||||
|
1/ 2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
4 2π |
1/ 2 |
|
|
C |
2 |
|||||
|
e |
ε |
0 |
|
|
|
|
|||
Если размерность ε – м/рад, радиуса а – м, численное значение всего множителя в первых скобках равняется 1,5·103. Тогда для тока 0,5 A ускоряющее напряжение 30·103 В и f = 0, эмиттанс преобладает при 1,2·10–3 , т.е. если a > 80ε во всех областях пучка, то пространственный заряд является главным ограничением ми-
36
нимального поперечного сечения пучка. В случае, когда a < 80ε, преобладающим фактором ограничения является эмиттанс. В приблизительно полностью скомпенсированном пучке (f ≈ 1) эмиттанс является главным фактором ограничения достижения высокой плотности тока и мощности до тех пор, пока соударения, расширения распределения энергии электронов, неоднородности материалов и аберрации делают его использование как характеристики пучка невозможным. Ионы в не полностью скомпенсированном интенсивном электронном пучке находятся в потенциальной яме с глубиной, пропорциональной первеансу. Они осциллируют вокруг положения равновесия, и становится возможным появление плазменных колебаний и неустойчивостей. Неравномерность катодной эмиссии, аберрации и другие нелинейные эффекты ведут к потере структуры пучка, описываемой параксиальным или другим идеализированным уравнением. Дальнейшее описание пучка следует делать статистическими методами, используя как характеристику поперечно двигающихся электронов температуру Te ≈ Tк·K, где K – это сжатие по площади пучка, Tк – это температура катода. При фокусировании пучка электронная температура Tк растет и электроны двигаются со скоростями, сильно наклоненными к оси z. Обобщенное описание такогопучкаявляетсянелегкойработой. Известенанализ некоторых специальныхслучаев.
1.1.8. Электронно-оптические аберрации
Часто в электронной оптике свойства электронного пучка анализируются через поведение отдельных электронов в ускоряющих и фокусирующих электрических и магнитных полях. Теоретически существуют уравнения, позволяющие найти траекторию электрона при условии, что известно распределение поля. Или решают обратную задачу нахождения поля, необходимого для обеспечения определенной формы пучка. Широко использованная аппроксимация в электронной оптике – это тон-
37

кий параксиальный пучок. Параксиальный пучок лучей – пучок лучей, распространяющихся вдоль оси центрированной оптической системы и образующих очень малые углы с осью. Если задана одна базовая траектория и распределение компонентов электрического и магнитного поля по ее длине, то становится возможным найти траектории соседних электронов. Отклонение электронов от этой базовой траектории (ось пучка) и угол между осью и рассчитанными траекториями принимаются малыми. Простейшие, но составляющие большинство среди электроннолучевых устройств – это прямолинейные устройства с осесимметричным электрическим полем. Обычно распределение потенциала вдоль оси симметрии известно (или относительно просто определяется). В цилиндрической системе координат (z, r, ϕ ) распределение потенциала в пространстве около оси можно представить через значение потенциала на самой оси U0 (z). После применения уравнения Лапласа для потенциала осесимметричного поля получено соотношение
U (z, r) = U0 |
− |
1 |
U |
0II (z)r 2 + |
|
|
|||||
|
4 |
|
|
|
|
|
|
|
|
∞ |
2k |
= (−1)k ∑ |
U0 |
||||
2 |
|||||
|
|
|
|
k =0 |
(k !) |
1 |
U0IV (z)r 4 − .... = |
|
|||
64 |
(1.17) |
||||
|
|
||||
r |
2k |
||||
|
|||||
|
|
, |
|
||
|
|
||||
2 |
|
|
|||
индексами II, IV и 2k обозначены соответствующие производные потенциала по z. Члены с нечетными степенями в разложении уравнения (1.17) отсутствуют в результате равенства потенциала в симметричных относительно оси точках. Когда электрон двигается вблизи оси z, принимается, что осевая составляющая поля не зависит от расстояния r до оси и радиальная составляющая является пропорциональной r, т.е. используется только самая низкая степень в ряде уравнений (1.17). Скорость электрона в тонком параксиальном пучке определяется как
V ≈ Vz |
= |
2e |
U |
0 ( z ) . |
|
||||
|
|
m |
|
|
38
Движение электрона в радиальном направлении записывают как
m |
d 2 r |
= − |
1 |
eU II (z)r . |
(1.18) |
dt 2 |
|
||||
|
2 0 |
|
|||
После исключения времени t из уравнения (1.18) траектория параксиального электрона с нерелятивистской энергией описывается дифференциальным уравнением
d 2 r |
|
U0I ( z ) dr |
|
U0II ( z ) |
|
|||
|
+ |
|
|
|
+ |
|
r = 0 . |
(1.19) |
dz2 |
2U0 ( z ) |
dz |
4U0 ( z ) |
|||||
Поскольку в формуле (1.19) заряды и массы частиц отсутствуют, траектории любых заряженных частиц в осесимметричном поле одинаковы. Существует разница во время движения. Уравнение линейно относительно потенциала, и поэтому при одновременной смене потенциала во всех точках пространства траектория не меняется. Решение уравнения (1.19) получено как сумма двух линейных независимых решений:
r ( z ) = C1r1 ( z ) + C2 r2 ( z ) , |
(1.20) |
где C1 и C2 – константы, определенные начальными условиями. Очевидно, что если поле неоднородно при U0II ( z ) > 0 , то первое частное решение может дважды принимать нулевые значения:
r1 ( zA ) = r1 ( zB ) = 0 . |
(1.21) |
При C2 = 0 и при соблюдении формул (1.20) и (1.21) получаются группы траекторий с началом в точке A (zA, 0), снова пересекающихся в точке B (zB, 0) на оси, т.е. B – это электроннооптическое изображение точки A. Если C2 ≠ 0, но условие (1.21) выполняется, все траектории, соответствующие некоторому значению C2 и для различных C1, проходят через точки S и I (рис. 1.9), которые не лежат на оси. Соответственно, точечный
39

источник S [zA,C2,r2 (zA)] проецируется в электронно-оптическом образе I [zB,C2,r2 (zB)]. Следовательно, любое неравномерное осесимметричное электростатическое поле, в котором U0II ( z ) > 0, действует как собирающая электронная линза.
Рис. 1.9. Электронно-оптические изображения I иB точекA иS: SS – плоскость предмета; IS – плоскость изображения; траектории:
1 – C1r1 (z) +C2r2 (z); 2 – C1I r1 ( z ) ; 3 – r1 (z); 4 – C1II r1 ( z ) ;
5 – C2r2 (z); 6 – C1II r1 ( z ) + C2 r2 ( z )
Аналогичное рассмотрение возможно и для осесимметричного магнитного поля. Основная разница в том, что магнитное поле придает азимутальную скорость и повернутое на некоторый угол по отношению к источнику изображение. Движение электронов в осесимметричном магнитном поле описывается следующей системой дифференциальных уравнений:
d 2 r |
|
|
e |
|
|
|||
|
|
|
= − |
|
|
B02 ( z )r ; |
(1.22) |
|
dz2 |
8mU0 ( z ) |
|||||||
|
dφ |
= |
|
e |
B0 ( z ) . |
(1.23) |
||
|
dz |
|
8mU0 ( z ) |
|||||
|
|
|
|
|
||||
40
