
Современные проблемы теории управления
..pdf
а также их хорошими алгебраическими свойствами, необходимыми для решения прикладных задач анализа и моделирования различных систем.
Нечеткие отношения. Операции с нечеткими множествами
Нечеткие отношения необходимы для организации нечетких выводов [23]. Предположим, что знание эксперта отражает нечеткое причинное отношение предпосылки A и заключения B, которое описывается нечетким R.
R = A → B,
гдеR – сила связимежду элементами предпосылкиизаключения. Почти все реально работающие прикладные системы, использующие промежуточные нечеткие оценки, это системы, основанные на нечетких продукционных правилах. Нечеткое отношение R между двумя множествами Х и Y будем называть нечетким множеством, определенным на декартовом произве-
дении Х·Y.
Пусть A1, A2,…, An – нечеткие подмножества универсальных множеств E1, E2,…, En. Тогда А = А1 × А2 × …× Аn – есть произведениеподмножеств, лежащихвуниверсумеE = E1 × E2 × …× En c ФП
μА (х1, х2,…, хn) = min{μА1 (х1), μА2 (х2),…, μАn (хn)}.
Формы записи нечеткого отношения:
R X*Y = {(xRy): x X, y Y} = {(x, y), μR (x, y)},
где μR (x, y) [0,1].
R = μR (x, y) .
X ×Y
151
В случае, когда X = Y, т.е. X и Y совпадают, нечеткое отношение R: (X*X) → [0,1] называется нечетким отношением на множестве Х.
Пусть X = { x1 , x2 , x3 }, Y = { y1 , y2 , y3 }.
Нечеткое отношение x R y может быть задано с помощью таблиц.
Нечеткое отношение
|
y1 |
y2 |
y3 |
x1 |
0,8 |
0,6 |
0,4 |
x2 |
1 |
0,8 |
0,6 |
x3 |
0,8 |
1 |
0,8 |
Другие формы представления отношений
Найти отношение подмножеств X = {3, 4, 5} и Y = {4, 5, 6},
где х1 = 3; х2 = 4; х3 = 5; у1 = 4; у2 = 5; у3 = 6. Их отношение:
«y примерно равен х».
Решение. Данное отношение можно записать в виде
R = |
1 |
+ |
1 |
+ |
0,8 |
+ |
0,8 |
+ |
0,8 |
+ |
0,6 |
+ |
0,6 |
+ |
0,4 |
|||||||||||
(4,4) |
(5,5) |
(3,4) |
(4,5) |
(5,6) |
(3,5) |
(4,6) |
(3,6) |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, |
|
если х = у; |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
если |
|
|
|
х− у |
|
|
= 1; |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
μR (x,y) = |
0,8, |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
если |
|
|
х− у |
|
|
|
= 2; |
|
|
|
|
|||||||||||
|
|
|
|
|
0,6, |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
если |
|
х− у |
|
|
= 3. |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
0,4, |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
152
Или
|
|
y1 |
y2 |
y3 |
||
х1 |
|
0,8 |
0,6 |
0,4 |
|
|
|
|
|||||
μR (x, y) = х2 |
|
1 |
0,8 |
0,6 |
|
. |
х3 |
|
0,8 |
1 |
0,8 |
|
|
Определить нечеткое отношение с помощью операции min при заданных нечетких множествах А и В.
|
0 |
|
0,1 |
|
0,5 |
|
0,8 |
1 |
|
1 |
0,8 |
|
0,4 |
|
0,2 |
|||
A = ( |
1 |
; |
2 |
; |
3 |
; |
4 ; |
5); |
B = (5 ; |
10 |
; |
15 |
; |
20 ). |
||||
Решение: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
0,1 |
0,1 |
0,1 |
0,1 |
|
|
|
|
|
|
|
|
|
|
|
R = |
|
0,5 |
0,5 |
0,4 |
0,2 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
0,8 |
0,8 |
0,4 |
0,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
0,8 |
0,4 |
0,2 |
|
|
|
|
|
|
Операции с нечеткими отношениями Пересечение
Пересечение двух отношений R1 и R2 обозначается R1 ∩ R2 и определяется выражением μR1 ∩R2 (x, y) = μR1 (x, y) ∩ μR2 (x, y).
Объединение
Объединение двух отношений обозначается R1 R2 и определяется выражением μR1 R2 (x, y) = μR1 (x, y) μR2 (x, y).
Алгебраическое произведение
Алгебраическое произведение двух отношений R1 и R2 обозначается R1 * R2 и определяется выражением
μR1 R2 (x, y) = μR1 (x, y)μR2 (x, y).
153

Алгебраическая сумма
Алгебраическая сумма двух отношений R1 и R2 обозначается R1 + R2 с выражением
μR1 + R2 (x, y) = μR1 (x, y) + μR2 (x, y) − μR1 (x, y) *μR2 (x, y).
Дизъюнктивная сумма двух отношений R1 и R2 обозначается R1 R2 и определяется выражением
R1 R2 = (R1 ∩ R2 ) (R1 ∩ R2 ).
Дополнение
ДополнениеотношенияR обозначается R иопределяетсяФП:
μR (x, y) = 1− μR (x, y).
Для введенных операций справедливы следующие свойства дистрибутивности:
R1 ∩ (R2 R3 ) = (R1 ∩ R2 ) (R1 ∩ R3 ),
R1 (R2 ∩ R3 ) = (R1 R2 ) ∩ (R1 R3 ),
R1 * (R2 R3 ) = (R1 * R2 ) (R1 * R3 ),
R1 * (R2 ∩ R3 ) = (R1 * R2 ) ∩ (R1 * R3 ),
R1 + (R2 R3 ) = (R1 + R2 ) (R1 + R3 ),
R1 + (R2 ∩ R3 ) = (R1 + R2 ) ∩ (R1 + R3 ).
Рассмотрим возможные варианты комбинаций:
1.Пересечение и объединение нечетких отношений:
μR1 ∩ R2 (x, z) = min (μR1 (x, y), μR2 ( y, z));
μR1 R2 (x, z) = max (μR1 (x, y), μR2 ( y, z)).
154
2. Произведение нечетких отношений рассмотрим на следующем примере. Пусть заданы отношения:
|
|
|
y1 |
y 2 |
|
|
|
z1 |
z 2 |
z 3 |
|
R1 |
= |
x1 |
0,2 |
0,5 |
; R2 = |
y1 |
0,3 |
0,6 |
0,8 |
, |
|
x2 |
|
1 |
|
y2 |
|
0,9 |
|
||||
|
|
0,6 |
|
|
0,7 |
0,4 |
|
||||
причем
Х = {x1 , x 2 }; Y = {y1 , y 2 }; Z = {z1 , z2 , z3}.
Решение:
y1 y 2 |
z1 z 2 z 3 |
q11 q12 q13 |
R = R1*R2 |
= |
x1 |
0,2 |
0,5 |
* |
y1 |
0,3 |
0,6 |
0,8 |
0,5 |
0,5 |
|
x2 |
|
1 |
|
y2 |
|
0,9 |
|
= |
0,9 |
|||
|
|
0,6 |
|
|
0,7 |
0,4 |
0,7 |
|||||
q 21 q 22
где q11 = max[min (0,2; 0,3), min (0,5; 0,7)] = 0,5; q12 = max[min (0,2; 0,6), min (0,5; 0,9)] = 0,5; q13 = max[min (0,2; 0,8), min (0,5; 0,4)] = 0,4; q 21 = max[min (0,6; 0,3), min (1; 0,7)] = 0,7; q 22 = max[min (0,6; 0,6), min (1; 0,9)] = 0,9; q 23 = max[min (0,6; 0,8), min (1; 0,4)] = 0,6.
Нечеткая импликация. Варианты реализации
0,4
0,4
q 23
Нечеткая импликация есть логическая операция отношения двух высказываний А и В в новое высказывание «Если А, то В» и обозначается RA→ B . В более общем смысле нечеткую им-
пликацию можно представить в виде нечетких множеств с ФП, заданной выражением [6, 15]:
RАЛ →BK : IF (x1 это A1K AND....AND xn это AnK ) THEN ( y это BK ).
155

Аналитическое выражение нечеткой импликации:
|
|
μR (x, y) |
|
– называетсяаналоговойнечеткойимпликацией. |
|
(x, y) |
|
||
X *Y |
|
|
|
|
|
μR (x, y) |
|
– называется цифровой нечеткой импликацией |
|
(x, y) |
|
|||
X *Y |
|
|
|
|
Правило четкой импликации
Бинарное правило (Клинс, 1938 г.) – четкая импликация S-типа:
μR A→ B (x, y) = [1− μA (x)] μB ( y) = max[1− μA (x),μB ( y)].
Правило нечеткой импликации
1.Правило типа «логическое произведение» (1965 г.) – импликация Т-типа по Заде – правило Заде:
μRА→В = [μA (x) ∩ μB (y)] [1− μA (x)] = max{min[μA (x),μB (y)],μA (x)}
2.Алгоритм Мамдани (1974 г.) – импликация Т-типа по Мамдани – правило Мамдани:
μRA→ B (x, y) = μА(x) ∩ μB ( y) = min[μA (x),μB ( y)].
3.Правило Лукашевича (1976 г.):
μRА→ B (x, y) = 1∩ [1− μA (x) + μB ( y)] = min[1; 1− μA (x) + μB ( y)].
4.Правило типа «алгебраическое произведение» (Ларсен, 1980 г.) – правило Ларсена:
μRA→ B (x, y) = μA (x) *μB ( y).
156
5. Правило Гогуэна, нечеткая импликация типа:
|
1, еслиμA (x) = 0, |
||||
μR |
|
μ |
|
( y) |
|
(x, y) = |
B |
;1), для других. |
|||
А→ B |
min( |
|
|
||
|
μA (x) |
||||
|
|
|
|||
6. Правило Шарпа:
μR A→B |
1, еслиμA (x) ≤ μB ( y); |
||
(x, y) = |
|
||
|
|
0, еслиμA (x) μB ( y). |
|
7. Правило Гёделя: |
|
||
μR A→ B |
|
1, еслиμA (x) ≤ μB (y); |
|
(x, y) = |
( y). |
||
|
|
μB ( y), еслиμA (x) μB |
|
8. Вероятностное правило (Рейшенбах) – импликация QL-типа:
μR A→ B (x, y) = 1∩ [1− μA (x) + μA (x)μB ( y)] =
=min[1,1− μA (x) + μA (x)μB ( y)].
Операцию «нечеткой импликация» в теории нечетких множеств можно реализовать по-разному (при этом будет отличаться и полученной результат): по Заде, Мамдани, Ларсену и т.д.
Нечеткая композиция. Аналитический способ свертки
Нечеткая композиция есть свертка логической информации после нечеткой импликации [6,15,16].
Существуют два способа композиции (свертки): аналитический и графический.
Аналитический способ композиции
Пусть R1: (X×Y) → [0,1]; R2: (Y×Z) → [0,1],
μR1·R2 (x, z) = [μR1 (x, y) ∩ μR2 (y, z)] – есть max-min ком-
позиция (сверстка) отношений R1 и R2.
157
Определить композицию:
R1 |
y1 |
|
|
y2 |
|
|
Y3 |
|
х1 |
0,1 |
|
|
0,7 |
0,4 |
|||
х2 |
1 |
|
|
0,5 |
0 |
|||
|
|
|
|
|
|
|
|
|
R2 |
|
Z1 |
Z2 |
z3 |
|
|
z4 |
|
y1 |
|
0,9 |
0 |
1 |
|
0,2 |
||
y2 |
|
0,3 |
0,6 |
0 |
|
0,9 |
||
y3 |
|
0,1 |
1 |
0 |
|
0,5 |
||
Тогда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R1· R2 |
|
z1 |
Z2 |
z3 |
|
|
z4 |
|
x1 |
|
0,3 |
0,6 |
0,1 |
|
0,7 |
||
х2 |
|
0,9 |
0,5 |
1 |
|
|
0,5 |
|
х2 = y1 = z3 – одни и те же числа.
Доказательство:
μR1·R2 (x1, z1) = [μR1 (x1, y1) |
∩ μR2 (y1, |
z1)] |
[μR1 |
(x1, |
y2) |
∩ μR2 (y2, z1)] |
|
|
|
|
|
[μR1 (x1, y3) ∩ μR2 (y3, z1)] = (0,1 ∩ 0,9) |
(0,7 ∩ 0,3) |
|
|||
(0,4 ∩ 0,1) = 0,1 |
|
|
|
|
|
0,3 0,1 = 0,3; |
|
|
|
|
|
μR1·R2 (x1, z2) = [μR1 (x1, y1) |
∩ μR2 (y1, |
z2)] |
[μR1 |
(x1, |
y2) |
∩ μR2 (y2, z2)] |
|
|
|
|
|
[μR1 (x1, y3) ∩ μR2 (y3, z2)] = (0,1 ∩ 0) |
(0,7 ∩ 0,6) |
|
|||
(0,4 ∩ 1) = 0 0,6 |
|
|
|
|
|
0,4 = 0,6; |
|
|
|
|
|
μR1·R2 (x1, z3) = [μR1 (x1, y1) |
∩ μR2 (y1, |
z3)] |
[μR1 |
(x1, |
y2) |
∩ μR2 (y2, z3)] |
|
|
|
|
|
158
[μR1 (x1, y3) ∩ μR2 (y3, z3)] = (0,1 ∩ 1) (0,7 ∩ 0) |
(0,4 |
||
∩ 0) = 0,1 0 0 = 0,1; |
|
|
|
μR1·R2 (x1, z4) = [μR1 (x1, |
y1) ∩ μR2 (y1, z4)] |
[μR1 |
(x1, y2) |
∩ μR2 (y2, z4)] [μR1 (x1, y3) ∩ μR2 (y3, z4)] = (0,1 |
∩ 0,2) |
(0,7 |
|
∩ 0,9) (0,4 ∩ 0,5) = 0,1 0,7 0,4 = 0,7; |
|
|
|
μR1·R2 (x2, z1) = [μR1 (x2, |
y1) ∩ μR2 (y1, z1)] |
[μR1 |
(x2, y2) |
∩ μR2 (y2, z1)] [μR1 (x2, y3) |
∩ μR2 (y3, z1)] = (1 |
∩ 0,9) |
(0,5 |
∩ 0,3) (0 ∩ 0,1) = 0,9 0,3 0 = 0,9; |
|
|
|
μR1·R2 (x2, z2) = [μR1 (x2, |
y1) ∩ μR2 (y1, z2)] |
[μR1 |
(x2, y2) |
∩ μR2 (y2, z2)] |
|
|
|
[μR1 (x2, y3) ∩ μR2 (y3, z2)] = (1 ∩ 0) (0,5 ∩ 0,6) (0 ∩ 1) = 0 0,5 0 = 0,5;
|
μR1·R2 (x2, z3) = [μR1 (x2, y1) ∩ μR2 (y1, z3)] |
[μR1 |
(x2, y2) |
|
∩ μR2 |
(y2, z3)] |
[μR1 (x2, y3) ∩ μR2 (y3, z3)] = (1 ∩ 1) (0,5 ∩ |
||
0) (0 ∩ 0) |
=1 0 0 = 1; |
|
|
|
|
μR1·R2 (x2, z4) = [μR1 (x2, y1) ∩ μR2 (y1, z4)] |
[μR1 |
(x2, y2) |
|
∩ μR2 |
(y2, z4)] [μR1 (x2, y3) ∩ μR2 (y3, z4)] = (1 |
∩ 0,2) |
(0,5 |
|
∩ 0,9) (0 ∩ 0,5) =0,2 0,5 0 = 0,5. |
|
|
||
Графический способ нечеткой композиции – поточечное суммирование ординат функций принадлежности после нечеткой импликации.
Свойства max-min нечеткой композиции
Операция max-min композиции – ассоциативна:
R3 *(R2 * R1 ) = (R3 * R2 )* R1 ,
дистрибутивна относительно объединения:
R1 *(R2 R3 ) = (R1 * R2 ) (R1 * R3 ) ,
159
дистрибутивна относительно пересечения:
R1 *(R2 ∩ R3 ) = (R1 * R2 ) ∩ (R1 * R3 ) .
Кроме того, для max-min-композиции выполняется следующее важное свойство (включение): если R1 R2 , то
R3 * R1 R3 * R2 .
Модуль нечеткого логического вывода
Для многих приложений, связанных с управлением технологическими процессами, необходимо построение модели рассматриваемого процесса. Знание модели позволяет подобрать соответствующий регулятор. Применение теории нечетких множеств для управления технологическими процессами не предполагает знание моделей этих процессов. Следует только сформулировать правила поведения в форме нечетких условных суждений типа.
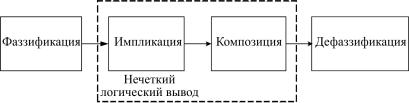
Рассмотрим структуру модуля «нечеткий регулятор», показанного на рис. 7.6, состоящего из фаззификатора, нечеткого логического вывода и дефаззификатора.
Рис. 7.6. Структурная схема модуля «нечеткий регулятор»
Система нечеткого логического вывода объединяет операции нечеткой импликации и нечеткой композиции.
Дефаззификатор преобразует нечеткую логическую информацию в четкую логическую информацию.
160
