Математика введение в анализ дифференциальное исчисление функции од

Например, при ε= 0,01 следует взять N =

4

= 400 ;

0, 01

тогда при x = 401 получим

f (x) − 3

=

4

=

4

< 0,01 ;

x

401

при ε= 0,0001надо будет взять

N =

4

= 40 000 и тогда при

0, 0001

x = 40 001 будем иметь

f (x) − 3

=

4

=

4

< 0, 0001.

x

40 001

Задача 3. Найти односторонние пределы функции

−2x −1,

x < 2

в точке x0 = 2.

f (x) =

x ≥

2

3x + 2,

Решение

Если

x < 2 ,

то

f (x) = −2x −1 ;

следовательно,

lim (−2x −1) = −5 – предел слева (рис. 2.10).

x→ −2 0

x ≥ 2 .

f (x) = 3x + 2 ;

Пусть

Тогда

следовательно,

Основные формулы

Определения

и рисунки

и замечания

1. Символическая записьбес-

Функция α( x) называется

конечномалойфункции α( x) :

бесконечно малой при x →

x ,

0

lim α( x) = 0

(2.38)

если

lim α( x) = 0 .

x→ x0

x→

x0

Замечание

Бесконечно малые функции

(б.м.ф.) часто называют беско-

нечно

малыми

величинами

и

обозначают греческими буква-

ми α( x) , β( x) , γ( x ) и т.д.

2. Символическая

запись

Определение

определения бесконечно малой

Функция α(x) называется

функции при x →

x0 :

бесконечно малой функцией при

lim α( x) = 0

x →

x0 , если для любого сколь

угодно малого числа ε > 0 , най-

x→

x0

(

)

дется такое положительное чис-

( >ε

0

δ>ε

0

x ,

ло δ , зависящее от ε, что для

0 <

x − x0

< δ

α( x)

< ε) (2.39)

всех

x ≠ x0

удовлетворяющих

неравенству

x − x

< δ

выпол-

0

няетсянеравенство

α( x )

< ε .

Замечание 1

Аналогично

определяются

б.м.ф.

при

x →

∞

,

x → +

∞ ,

x → − ∞ , x → x+ 0

, x → x− 0 .

0

0

Замечание 2

Бесконечно малая функция

есть функция ограниченная.

3. Если

lim α( x) = 0 ,

Если две функции

α( x) и

x→ x0

β( x) – бесконечно малые в точ-

lim β( x) = 0 , то

ке x0, то и сумма их бесконечно

x→ x0

lim [α( x ) + β(x)] = 0

(2.40)

малая в точке x0.

Замечание

x→ x0

остается

Это

свойство

справедливым для любого ко-

нечного числа n слагаемых.

4. Если

lim α( x) = 0 ,

Если

в

точке x0

функция

x→ x0

α( x) бесконечно малая, а функ-

f ( x)

≤ M , то

ция f (x)

ограничена в окрест-

lim α( x) f (x) = 0

(2.41)

ности точки x0, то произведение

x→ x0

их

f ( x) α( x)

есть

функция

бесконечно малая вточкеx0.

5. Если C = const ,

Произведение числа

C на

lim α( x) = 0 , то

бесконечно

малую функцию

x→ x0

в точке x0 есть функция беско-

lim C α( x) = 0

(2.42)

нечно малая в точке x0.

x→ x0

6. Если

lim α( x) = 0 ,

Частное от деления функ-

x→ x0

ции α( x) ,

бесконечно

малой

lim

f ( x) = A ≠ 0 , то

в

точке x0,

на функцию

f (x) ,

x→ x0

α( x)

имеющую предел в точке x0, от-

= 0

lim

f (x)

(2.43)

личный от нуля,

есть

функция

x→ x0

бесконечно малая вточкеx0.

7. Если

lim α( x) = 0 ,

Произведение двух

беско-

x→ x0

нечно малых функций в точке x0

lim β( x) = 0 , то

есть функция бесконечно малая

x→ x0

в точке x0.

lim α( x) β(x) = 0

(2.44)

Замечание 1

x→ x0

Это справедливо для любо-

го конечного числа множителей.

Замечание 2

Формулы (2.40)–(2.44) спра-

ведливы

для

случаев:

x →

∞ ,

x → + ∞ ,

x → −

∞ .

Связь между функцией, её пределом и бесконечно

малой функцией

8. Если lim f ( x) = A , то

Если

функция

f (x)

при

x→ x0

x →

x0 имеет предел,

равный A,

f ( x) = A + α( x )

(2.45)

то её можно представить как

сумму числа A и бесконечно ма-

лойфункции α( x) при x →

x .

0

9. Если f ( x) = A + α( x) , то

Обратное утверждение: ес-

lim f ( x) = A

ли функцию f (x)

можно пред-

(2.46)

ставить в виде суммы числа A

x→ x0

и

бесконечно

малой

функции

α( x) при

x →

x

,

то число A

0

является

пределом

функции

f (x) при x →

x0 .

Замечание

Утверждения (2.45) и (2.46)

справедливы

для

случаев:

x → ∞ , x → − ∞ , x → +

∞ .

10. Символическая

запись

Замечание

бесконечно большой функции

Функция

y = f ( x) ,

являю-

f (x) :

щаяся при

x

→

x0

бесконечно

lim f ( x) = ∞

(2.47)

большой

величиной,

не имеет

x→ x0

пределав обычном смысле.

f (x)

Говорят, что функция

при x →

x0

стремится к беско-

нечности или имеет своим пре-

деломбесконечность.

11. Символическая

запись

Определение (на «языке

определения

бесконечно

боль-

M – δ »)

шой функции при x → x0 :

Функция y = f (x) называет-

lim f ( x) = ∞

ся бесконечно большой (б.б.ф.)

x→

x0

в точке x0, если для любого

(

>M

0

δ(M> )

0,

сколь

угодно

большого числа

x, 0<

x− x0<

δ

M > 0

существует такое число

(2.48)

δ , зависящее от M, что для

f ( x)

> M )

всех x, удовлетворяющих усло-

вию 0 <

x − x0

< δ, выполняет-

ся неравенство

f ( x)

> M .

Замечание

Подразумевается, что функ-

ция определена в некоторой ок-

рестности точки x0, за возмож-

ным исключением самой этой

точки.

12.

Замечание 1

На языке геометрии опреде-

ление бесконечно большой функ-

ции выглядит следующим обра-

зом: функция

f (x) называется

бесконечно большой в точке x0,

если для любой горизонтальной

полосы (−M ; M ) , сколь бы ши-

рокой она ни была, можно по-

добрать такие две вертикальные

прямые x = x0 − δ и x = x0 + δ ,

что между этими прямыми гра-

Рис. 2.11

фик функции

расположен вне

указаннойполосы(рис. 2.11).

Замечание 2

Иногда применяют обозна-

чения:

lim f ( x) = +∞

и

x

→ x0

lim

f ( x) = −∞ .

x→ x0

Эти записи означают, что

функция

f (x) бесконечно боль-

шая в точке x0, причем в неко-

торой окрестности точки x0 либо

она положительна, либо соот-

ветственно отрицательна.

Замечание 3

Всякая бесконечно большая

функция в окрестности точки x0

являетсянеограниченной.

13. Символическая

запись

Определение (на «языке

определения

бесконечно

боль-

M − N »)

шой функции при x → ∞

:

Функция y = f ( x)

назы-

lim f ( x)

= ∞

вается

бесконечно

большой

при x →

∞ , если для любого

x→∞

0 N (M> )

(

>M

0,

сколь угодно большого числа

f ( x)

M > 0 найдется

такое

число

x,

x>

N

> M )

(2.49)

N > 0 , зависящее от M, что для

всех x, удовлетворяющих ус-

ловию

x

> N ,

выполняется

неравенство

f (x)

> M .

Замечание

Геометрическая

иллюстра-

ция бесконечно большой функ-

ции, когда

x → +

∞

, показана

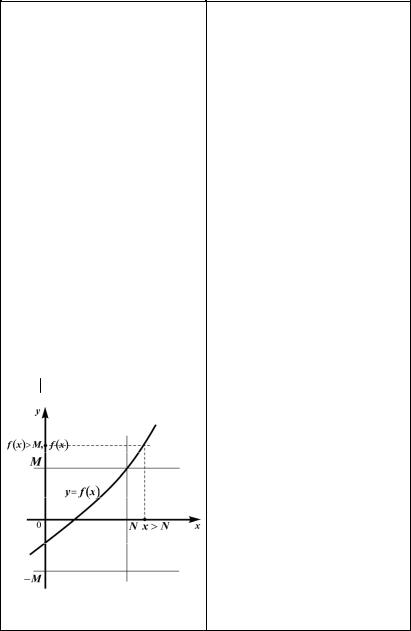
на рис. 2.12.

14. Если

lim

f ( x) = ∞

,

Сумма

двух

бесконечно

lim g ( x) = ∞

x→ x0

больших функций одинакового

, то

знака в точке x0 есть бесконеч-

x→

x0

но большая функция того же

lim [ f ( x) + g ( x)] = ∞

(2.50)

знака в точке x0.

x→

x0

15. Если lim

f ( x) = ∞

,

Сумма бесконечно большой

x→ x0

функции в точке x0 и функции

g( x)

≤ M , то

ограниченной

в

окрестности

lim [

f ( x) + g ( x)] = ∞

(2.51)

точки x0 есть бесконечно боль-

x→

x0

шая функция

того же

знака

в точке x0.

16. Если lim

f ( x) = ∞

,

Произведение

двух

беско-

x→ x0

нечно больших функций в точ-

lim g ( x) = ∞

,

ке x0 есть функция бесконечно

x→

x0

большая в точке x0.

то lim f ( x) g(x) = ∞

(2.52)

x→

x0

17. Если

lim

f ( x) = +∞ ,

Произведение

числа

k на

k > 0 , то

x→ x0

бесконечно большую функцию

в точке x0 есть функция беско-

lim k f ( x) = +∞

(2.53)

нечно большая в точке x0.

x→

x0

Замечание

Формулы (2.50)–(2.53) спра-

ведливыидля случая x → ∞ .

Связь между бесконечно малой

и бесконечно большой функциями

18. Если

lim

f ( x) = ∞

, то

Если функция

f (x)

беско-

x→ x0

нечно большая

в

точке

x0, то

1

= 0

lim

(2.54)

функция

1

бесконечно ма-

f ( x)

x→

x0

f

( x)

лая в точке x0.

19. Если

lim α( x) = 0 , то

Если функция α(x)

беско-

x→ x0

нечно малая в точке x0, не рав-

lim

1

= ∞

(2.55)

ная нулю при

x ≠ x0 ,

то функ-

α( x)

x→ x0

1

ция

бесконечно большая

α( x)

в точке x0.

Замечание

Формулы (2.54) и (2.55) спра-

ведливы

и

для

случаев:

x → x+ 0 , x → x− 0 ,

0

0

x → ∞ , x → + ∞ , x → − ∞ .

Задачи

Задача 1. Доказать, что функция f (x) = 5x −15 при x →

3

является бесконечно малой.

Решение

f ( x) бесконечно малая, если

lim f ( x) = 0 ,

Функция

т.е.

x→ x0

зависящее

от

ε , что из неравенства

0 <

x − 3

< δ

следует

f ( x)

< ε.

Другими словами,

необходимо решить неравенство

5x −15

= 5

x − 3

< ε

или

x − 3

< ε . Если в качестве δ взять лю-

5

бое число ≤

ε

(т.е.

δ≤ ε ), то из неравенства

x − 3

< δ

следует

5

5

справедливость неравенства

f ( x)

< ε.

lim (5x −15) = 0 ,

Значит δ

существует, следовательно,

т.е.

функция f (x) = 5x −15 при x →

x→ 3

3 бесконечно малая.

Задача 2.

Доказать, что функция f (x) =

sin x

при

x →

∞

x

Так как x → ∞ , то функция

φ(x) =

1

бесконечно малая

x

функция (формула 2.54); действительно, lim

1

= 0 .

x

x→∞

Функция g(x) = sin x ограничена:

sin x

≤ 1,

x .

Значит, f (x) бесконечно малая при x → ∞ , т.е.

lim sin x = 0 .

x→∞

x

а)

lim 3x cos 2x ;

x→−∞

б)

lim x log4 x ;

x→+∞

в)

lim (2x

+ 5x ) ;

x→−∞

(−8x + log 1 x) ;

г)

lim

x→+∞

2

д)

lim ( x2

+ arctg x) ;

x→+∞

е)

lim

log1

x

3

.

x

x→+ 0

Решение

а) Из школьного курса известно,

что 3x > 0 возрастающая.

И при x →

–∞

3x →

0 , значит,

lim 3x = 0

, следовательно, 3x –

бесконечно малая функция.

x→−∞

Функция

cos 2x

ограничена, так как

cos 2x

≤ 1 . Тогда по

формуле (2.41).

lim 3x cos 2x = 0 .

x→−∞

б) При

x → +∞

функция

log4 x

бесконечно большая (см.

lim log4 x = +∞ .

x→+∞

Согласно формуле (2.52)

lim x log4 x = +∞ .

x→+∞

в) Функция 2x

> 0 возрастающая. И при x →

–∞

2x →

0 ,

значит,

lim 2x = 0

, следовательно,

2x – бесконечно малая

x→−∞

функция,

5x

– бесконечно малая функция (доказывается аналогично).

Тогда по формуле (2.40) функция (2x + 5x )

при

x →

–∞

бесконечно малая, т.е. lim (2x + 5x ) = 0 .

x→−∞

lim (−8x) = −∞ .

г)

Согласно формуле (2.53)

Функция

log 1 x при x → +∞

x→+∞

– бесконечно большая (см. графики элемен-

2

тарных функций – глава 1, §3, рис. 1.26), т.е. lim log 1 x = −∞ .

x→+∞

2

Тогда по формуле (2.50) получаем, что сумма двух беско-

нечно больших функций одинакового знака есть функция бес-

конечно большая того же знака, т.е.

lim (−8x + log1 x) = −∞ .

x→+∞

2

д)

При

x → +∞

функция x2

бесконечно большая, т.е.

lim x2

= +∞

(формула 2.52, так как

x2 = x x ).

x→+∞