Математика введение в анализ дифференциальное исчисление функции од

Следует запомнить:

если функция y = f (x)

описыва-

ет какой-либо физический про-

цесс, то производная

y′

есть

скорость протекания этого про-

цесса. В этом состоит физиче-

ский смысл производной.

6.

Пусть прямая L,

проходя-

щая через точку M0, обладает

следующим

свойством:

если

точка M при перемещении её по

кривой C неограниченно при-

ближается к точке M0 (с любой

её стороны), то угол между

прямой L и секущей M0M стре-

мится к нулю. Тогда эта пря-

мая L называется касательной

Рис. 3.1

к кривой C в точке M0 (рис. 3.1).

Следует запомнить:

касательная к кривой C в точке x0

есть прямая, занимающая пре-

дельное положение секущей MM0

при стремлении точки M по кри-

вой C к точкеM0.

Линия C – график функции

y = f (x) , где

f (x) – непрерыв-

ная в точке x0 и некоторой её

окрестности функция.

Точка x0 + ∆ x принадлежит

этой окрестности (рис. 3.2).

kсек

=

∆

y

= tgβ,

(3.8)

kсек – угловой коэффициент

секущей,

проведенной

через

∆

x

точку М0 и точку М графика

функции

y = f (x)

с абсциссой

x0 + ∆ x .

α

– угол, который образует

касательная с положительным

направлением оси OX.

β – угол, который образует

секущая с положительным на-

правлением оси OX.

Следует запомнить:

kкас

= tgα = lim tgβ =

производная функции

f (x)

в точ-

ке x0 равна тангенсу угла наклона

∆ x→

0

(3.9)

∆

y

= lim

= f ′(x0 ),

касательной, проведенной

к гра-

∆

x

фику функции y = f (x)

в точке

∆ x→

0

f ′(x0 ) = tgα,

M 0 (x0 , f ( x0 )) .

(3.10)

Установленный

геометри-

ческий

смысл

производной

коротко формулируется так:

Значение производной

f ′(x0 )

равно

угловому коэффициенту

f ′(x ) = k

кас

(3.11)

касательной, проведенной к гра-

0

фику функции y = f (x) в точке

с абсциссой x0.

7.

Касательная

к

графику

функции

y = f (x)

в

некото-

рой его точке M 0 ( x0 , y0 ) , где

y0 = f ( x0 ), есть прямая,

прохо-

дящая через эту точку и имею-

щая угловой коэффициент kкас ,

равный f ′(x0 ) (см. п. 6).

Замечание

С

помощью

производной

Рис. 3.3

легко

решить важную

задачу

аналитической геометрии – за-

дачу о

нахождении уравнения

касательной к кривой y = f (x) .

Координаты точки касания М0

считаются заданными:

x = x0 ,

y = y0 = f ( x0 ).

y − y0 = f ′( x0 )( x − x0 )

– (3.12)

Уравнение любой прямой,

проходящей через данную точ-

уравнение касательной.

ку

M 0

( x0 , y0 ) в заданном на-

правлении, определяемом уг-

ловым

коэффициентом

k,

y − y0 = k ( x − x0 ),

где

k опре-

деляется по формуле (3.11).

8.

Нормалью к кривой назы-

y − y0 = −

1

( x − x0 ) – (3.13)

вается прямая, проходящая че-

f ′( x0 )

рез точку касания перпендику-

уравнение

нормали

к

графику

лярно касательной (рис. 3.3)

функции

y = f ( x)

в

данной

Замечание

Угловой коэффициент нор-

точке M 0 ( x0 , y0 )

мали kн связан с угловым ко-

1

1

эффициентом

касательной

kн = −

= −

(3.14)

k

= f

′( x ) условием перпен-

kкас

f ′( x0 )

кас

0

дикулярности.

9.

Следует запомнить:

направление кривой в

каждой

её точке определяется направ-

лением

касательной

к

ней

в этой точке.

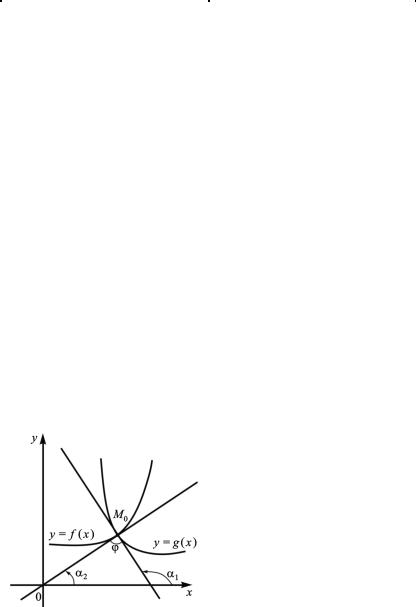
Угол ϕ между двумя пере-

секающимися кривыми опреде-

ляется как угол между двумя

прямыми, касательными к кри-

вым в точке их пересечения, по

формуле (3.15).

Рис. 3.4

tgφ =

k1 − k2

,

(3.15)

1 + k k

2

1

где

k

= tgα

=

dg(x)

=

k1

– угловой коэффициент

1

1

dx

x=x0

касательной к кривой y = g(x)

= g′( x

),

(3.16)

в точке M 0 (x0 , g ( x0 )) .

0

а k2 = tgα2 =

df (x)

=

k

2

– угловой коэффициент

dx

x=x0

касательной к кривой y = f (x)

= f ′( x0 ) .

(3.17)

в точке M 0 (x0 , f ( x0 )) .

10. Связь

между

непре-

Теорема

рывностью и дифференцируе-

Если функция y = f (x) диф-

мостью функции.

ференцируема в точке x = x0 , то

онав этойточкенепрерывна.

Следует запомнить:

обратная теорема неверна: суще-

ствуют

непрерывные функции,

которые в некоторых точках не

являются

дифференцируемыми

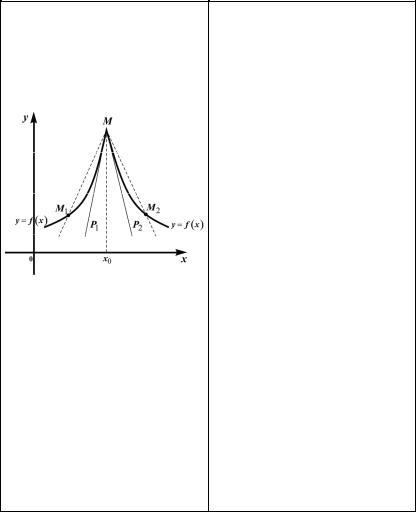
(рис. 3.5).

f+′(x) =

f+′(x) – правосторонняя про-

изводная или правая производная

=

lim

f (x + ∆ x)−

f (x)

(3.18)

функции

f (x) вточкеx.

∆ x

∆ x→+

0

f−′(x) =

f−′(x)

– левосторонняя про-

f (x + ∆ x)−

f (x)

изводная или левая производная

=

lim

(3.19)

функции

f (x) в точке x.

∆ x

∆ x→−

0

Замечание 1

f+′(x)

и f−′(x) называют

односторонними

производны-

ми функции f (x)

в точке x.

f (x + ∆ x)= (x+ ∆ x)= x+ 3x ∆ +x 3∆x( x+) ∆ ( x)

3

;

3

3

2

2

2) определим приращение функции y = f (x) = x3 , соответст-

вующее приращению аргумента на величину ∆ x :

∆ y= f (x+ ∆ x−)

f (x=)

x+

3x ∆ +x 3∆x(

+x) ∆ (

x−)

= x

∆ x+ 3x∆(

3

2

2

3

3

= 3x

2

x)+ ∆(

x)

;

2

3

3) найдем отношение приращения функции ∆

y к прираще-

нию аргумента ∆ x:

∆ y

=

3x2 ∆ +x 3x∆( x+)2 ∆ ( x)3

= 3x2 + 3x ∆ x+ (∆ x)2 ;

∆ x

∆

x

4) вычислим производную

f ′(x) =

dy

, т.е. найдем предел

∆ y

,

когда∆ x стремитсяк нулю:

dx

∆ x

f ′(x) = lim

f (x + ∆ x)−

f (x)

=

lim∆

y

=

∆ x

∆ x→

0

∆ →

x 0∆ x

= lim

3x

2

+ 3x ∆

x+

∆(

x)

2

3x

2

.

=

∆ x→ 0

Итак, для функции

f (x) = x3

производной является функция

f ′(x) = (x3 )′ = 3x2 .

Так, при x = 5 производная

f ′(5) = 3 52 = 75,

при x = (−2) про-

изводная

f ′(−2) = 12 и т.д.

б) Для функции y = sin x

дадим аргументу x приращение ∆

x , тогда:

1)

f (x + ∆ x)=

sin(x+ ∆

x);

2)

∆ y=

f (x+ ∆

x−) f (x=)

sin(+x ∆ −x)

sin x, откуда, восполь-

зовавшись формулой разности синусов двух углов

α = x + ∆ x

и β = x, имеем

(x + ∆ x)− x

(x+ ∆ x+) x

∆ x

∆

x

∆ y=

2sin

cos

=

2sin

cos x+

;

2

2

2

2

∆

x

cos

∆

x

∆ x

∆

y

2sin

x +

sin

∆

x

2

2

2

3)

=

=

cos x +

;

∆

∆ x

∆

x

x

2

∆ x

2

∆ y

sin

∆ x

2

4)

y′= lim

= lim

lim cos x +

,

∆ x→

0 ∆ x

∆ →

x 0

∆ x∆ →

x 0

2

2

Далее, поскольку при ∆ x→

величина

∆ x

→ 0

, то в соот-

0

2

ветствии сформулойпервогозамечательного предела

∆ x

sin

lim

2

=1,

∆

x

∆ x→ 0

2

а второй предел

lim cos

x +

∆ x

= cos x.

∆ x→ 0

2

ределяется уравнением (3.13).

Так как f ′(x ) = f ′(1) = −2 , следовательно,

−

1

=

1

.

0

f ′(1)

2

Получаем уравнение искомой нормали:

y + 3 =

1

(x −1) или

2

y =

x

−

7

.

2

2

tgα =

0 − (−1)

=1,

1 + 0 (−1)

α= 45° ,

tgβ =

−1 − (−2)

=

1

,

1

+ (−1)(−2)

3

β≈ 18,°5 .

Задача 4. Найти

f−′(0)

и

f+′(0)

для функции f (x) =

x

.

Решение

f+′(0)

f−′(0)

Для нахождения

и

используем формулы (3.18)

и (3.19):

f ′(0)

= lim

∆ x

= lim

−∆ x = −1,

−

∆ x→−

0

∆ x ∆ →− x

0 ∆ x

f ′(0) = lim

∆ x

=

lim

∆ x

=1.

+

∆ x→+

0 ∆ x ∆ →+x

0∆ x

Заметим, что функция

f (x) =

x

непрерывна для любого x,

в том числе и при x = 0 (рис. 3.8).