Экономические задачи линейного программирования и их решение с испол

2.В любой оптимальной задаче должны быть ограничения.

Вреальной экономике существует множество ограничений. Необходимо выбрать наиболее существенные ограничивающие условия. Обычно это ресурсы, спрос на продукцию.

3.Должна обеспечиваться свобода выбора, т.е. множество вариантов планирования.

4.Критерий оптимальности (цель) и ограничения должны быть записаны в линейной форме. Ограничения на ресурсы будут иметь линейную форму, если затраты ресурсов прямо пропорциональны объему производства. Это довольно жесткое условие.

Методы и модели линейного программирования применяются во всех отраслях народного хозяйства: при определении оптимального ассортимента выпускаемой продукции, при использовании взаимозаменяемых ресурсов, при разработке производственной программы предприятия, в задачах планирования и управления производством и финансами, при планировании грузо- и пассажиропотоков и т.д.

1.2. Постановка задачи линейного программирования

В общем виде задача линейного программирования может быть сформулирована как задача нахождения набора n переменных (х1, х2, х3, …, хn), максимизирующего линейную форму этих переменных:

zc1x1 c2 x2 ... cn xn max

иудовлетворяющего системе ограничений

где m < n.

11

Это каноническая форма задачи линейного программирования. Следует заметить, что тип искомого экстремума (максимума или минимума) носит относительный характер. Так, задача поиска

максимума функции

n

f (x) c j x j

j 1

эквивалентна задаче поиска минимума функции

n

f (x) ( c j )x j .

j 1

Если все ограничения в задаче линейного программирования являются уравнениями и на все переменные xj показываются условия неотрицательности, то она называется задачей линейного программирования в канонической форме или канонической задачей линейного программирования:

n

z c j x j min (max),

x j 0 ( j 1, n).

Если все ограничения в задаче линейного программирования являются неравенствами и на все переменные xj показываются условия неотрицательности, то она называется задачей линейного программирования в стандартной форме:

n

z c j x j min (max),

x j 0 ( j 1, n).

12

Если ограничения в задаче линейного программирования являются неравенствами и уравнениями, то она называется задачей линейного программирования в общей форме:

Условимся относительно обозначений, которые используются в дальнейшем и являются общепринятыми для решения множества экономических задач:

–z – целевая функция на максимум (минимум);

–bi – объем ресурсов, bi 0;

–хj – количество произведенной продукции разных видов;

–сj – коэффициенты эффективности (цена, прибыль от единицы продукции);

–аij – норма расхода i-го ресурса на единицу j-й продукции. Набор переменных (х1, х2, …, хn), удовлетворяющий условиям

(1.1), (1.2), называется планом. Таких планов множество, так как число уравнений меньше, чем число переменных. Множество всех планов составляет выпуклую область определения D. Область определения выпуклая, если отрезок, соединяющий две точки области, лежит внутри области (рис. 1.3, а) на рис. 1.3 б показана невыпуклая область определения. План является опорным, если он соответствует вершине области определения.

13

Переменные, вносимые в задачу при помощи этих утверждений, называются дополнительными. Они вносятся в целевую функцию с коэффициентом, равным нулю. Введение в задачу дополнительных неотрицательных переменных позволяет все ограничениянеравенства заменить ограничениями-равенствами. При этом число дополнительных переменных равно числу ограничений-неравенств в исходной задаче.

Пример Постановка задачи. Завод может выпускать два вида продук-

ции, А и В, в любом соотношении и количестве. Для производства продукции необходимо три вида ресурса (сырье, рабочая сила, оборудование), количество которого ограничено. Исходные данные задачи представлены в табл. 1.1.

Определить, какой ассортимент продукции необходимо выпускать, чтобы прибыль была максимальной.

Моделирование:

Этап 1. Обозначим неизвестные переменные. Пусть х1 – количество выпускаемой продукции А, х2 – количество выпускаемой продукции В.

Этап 2. Запишем целевую функцию на максимум суммарной прибыли:

z = 3x1 + 2,5x2 → max.

15

Этап 3. Запишем систему ограничений. Система ограничений на расход каждого вида ресурса примет вид:

6x1 3x2 60,1x1 2x2 20,0x1 2x2 20,

где левая часть – затраты ресурса, правая часть – запас ресурса. Этап 4. Запишем условие неотрицательности переменных:

x1, x2 ≥ 0.

Таким образом, получим следующую модель задачи: z = 3x1 + 2,5x2 → max,

6x1 3x2 60,1x1 2x2 20,0x1 2x2 20,

x1, x2 ≥ 0.

1.3. Графический метод решения задач линейного программирования.

Геометрическая интерпретация

Рассмотрим задачу линейного программирования с двумя переменными. Пусть дана задача максимизации линейной целевой функции

zc1x1 c2 x2 max

исистема ограничений в виде неравенств:

16

Такая задача может быть решена графически ввиду того, что ее можно отобразить на плоскости. Область определения представляет собой многоугольник (ограниченный или нет, либо вовсе пустое множество), стороны которого лежат на прямых, полученных из системы ограничений задачи (рис. 1.4, единственное решение).

Рис. 1.4

На рисунке показано, что каждое неравенство определяет некоторую полуплоскость. Соответствующие области для каждого ограничения отмечены штрихами. Пересечение данных полуплоскостей (т.е. множество точек, которые одновременно принадлежат каждой их них) является областью определения D (допустимых планов задачи). Необходимо выбрать из всех точек одну, которая дает максимальное значение z.

Поведение целевой функции z = c1х1 + c2х2 в рамках двумерной иллюстрации может быть охарактеризовано с помощью линий уровня α. Линией уровня функции называется множество точек из ее области определения, в которых функция принимает одно и то же фиксированное значение.

Градиентом функции z называется вектор, перпендикулярный линиям уровня и указывающий направление наискорейшего возрастания функции.

Если придать целевой функции конкретное постоянное значение α, то прямая c1x1 + c2x2 = α перпендикулярна нормальному векто-

17

ру n = (с1, с2). Для различных α будем иметь семейство параллельных прямых, перпендикулярных вектору n, причем значение α уве-

личивается в направлении вектора n.

Геометрическая интерпретация целевой функции z – это се-

мейство прямых, перпендикулярных нормальному вектору n, где

целевая функция принимает постоянное значение и увеличивается в направлении этого вектора n.

Геометрическая интерпретация системы ограничений (это неравенства (1.3) и (1.4)) – полуплоскости.

Область определения D – общая часть всех полуплоскостей.

Сгеометрической точки зрения задача максимизации сводится

копределению такой точки области D, через которую проходит линия

уровня , соответствующая наибольшему из возможных значений. Последнее означает, что для нахождения точки экстремума мы должны сначала построить линию уровня для некоторого произвольного значения целевой функции , затем осуществлять ее параллельное передвижение (так, чтобы она оставалась перпендикулярной вектору n ) до тех пор, пока она не достигнет крайней точки области D (из которой смещение в направлении вектора n невозможно). Такой метод решения получил название графического. На рис. 1.4 в точке А целевая функция принимает наибольшее значение, и она принадлежит области D, т.е. точка А соответствует оптимальному решению. Заметим, что решение задачи поиска минимума линейной функции осуществляется аналогично, с той лишь разницей, что движение по линиям уровня должно производиться в направлении, обратном градиенту целевойфункции, т.е. повектору (– n ).

Таким образом, получаем алгоритм решения с помощью графического метода:

1.Строим область допустимых решений D.

2.Строим вектор n = (с1, с2).

3.Строим линию уровня α, перпендикулярную вектору n.

4.При решении задач на максимум перемещаем линию уровня α

внаправлении вектора n до тех пор, пока она имеет общие точки

18

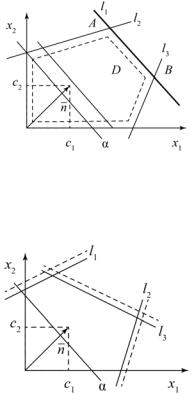
с областью D, т.е. находим крайнее положение (если оно существует), в котором линия уровня касается области допустимых решений. Вслучае решения задачи на минимум линию уровня перемещают

внаправлениивектора(– n ).

5.Определяем оптимальный план х* и экстремальное значение целевой функции z* = z(x*).

Возможно возникновение различных ситуаций решения:

1)единственное решение – оптимальное решение совпадает

свершиной D (см. рис. 1.4);

2)множество решений – оптимальное решение совпадает со стороной многоугольника (рис. 1.5);

Рис. 1.5

3) нет решения – область определения пуста, у полуплоскостей нет ни одной общей точки (рис. 1.6), или область определения не замкнута (рис. 1.7).

Рис. 1.6

19