
Экономические задачи линейного программирования и их решение с испол
..pdf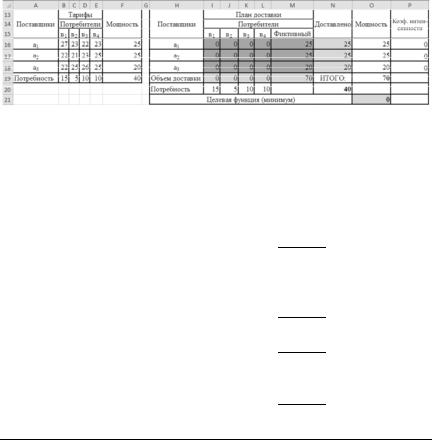
Рис. 3.30
Находим оптимальный план для этой модели с помощью надстройки Поиск решения. Алгоритм решения транспортной задачи представлен в подразд. 1.6. Оптимальные поставки отображены втабл. 3.9 (итерация1).
Поставщики |
|
|
|
Потребители |
|
|||
|
|
|
|
|
|
|
|
|
|
b1 |
b2 |
|
b3 |
b4 |
|
Фиктив- |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
ный |
а1 |
|
0 |
0 |
|
10 |
10 |
|
5 |
а2 |
|
0 |
5 |
|
0 |
0 |
|
20 |
а3 |
|
15 |
0 |
|
0 |
0 |
|
5 |
Объем |
|
15 |
5 |
|
10 |
10 |
|
30 |
доставки |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
Потребность |
|
15 |
5 |
|
10 |
10 |
|
– |
|
|
Целевая |
функция (минимум) |
|||||
|
Таблица 3.9 |
||
|
|
|
|
Дос- |
Мощ- |
Коэффи- |
|
циент |
|||
тавле- |
|||
но |
ность |
интен- |
|
|
|
сивности |
|
25 |
25 |
0,8 |
|
25 |
25 |
0,2 |
|
20 |
20 |
0,75 |
|
Итого |
70 |
|
|
40 |
|
|
|
|
|
||
|
885 |
|
|
Затем определяем коэффициент интенсивности для каждой строки. Строка с минимальным коэффициентом будет переходной. В нашем случае минимальный коэффициент k = 0,2 у поставщика а2. Это означает, что в пункте а2 рассмотрим другой вариант строительства с меньшей мощностью – 20 т. Соответственно, меняются затраты в этой строке и спрос фиктивного потребителя. Снова решаем транспортную задачу с помощью надстройки Поиск решения, но уже с новыми данными. Результаты нового расчета приведены в табл. 3.10 (итерация 2).
151
Таблица 3.10
|
|
Потребители |
|
Дос- |
Мощ- |
Коэффи- |
|||
Поставщики |
|
|
циент |
||||||
|
|
|
|
|
|
тав- |
|||
|
|
|
|
|
|
ность |
интен- |
||
|
|
|
|
|
Фик- |
||||
|
b1 |
b2 |
b3 |
b4 |
|
тивный |
лено |
|
сивности |
а1 |
0 |
0 |
10 |
10 |
|
5 |
25 |
25 |
0,8 |
а2 |
0 |
5 |
0 |
0 |
|
15 |
20 |
20 |
0,25 |
а3 |
15 |
0 |
0 |
0 |
|
5 |
20 |
20 |
0,75 |
Объем |
15 |
5 |
10 |
10 |
|
25 |
Итого |
65 |
|
доставки |
|
|
|||||||
Потребность |
15 |
5 |
10 |
10 |
|
|
40 |
|
|
Целевая функция (минимум) |
|
890 |
|
||||||
Наименьший коэффициент интенсивности имеет снова поставщик а2. По этой строке переходим к следующему варианту с мощностью 15 т и корректируем затраты и спрос фиктивного потребителя. Информацию заносим в табл. 3.11 (итерация 3) и снова определяем оптимальный план и т.д., пока все коэффициенты интенсивности не примут целое значение 0 или 1. Для решения данной задачи потребовалось четыре итерации (табл. 3.12).
Таблица 3.11
|
|
|
|
Потребители |
|
Дос- |
|
Коэф- |
|||
|
|
|
|
|
Мощ- |
фициент |
|||||
Поставщики |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
тавле- |
интен- |
|||
|
|
|
|
|
|
Фик- |
ность |
||||
|
|
b1 |
b2 |
|
b3 |
b4 |
|
тивный |
но |
|
сивно- |
|
|
|
|
|
|
|
|
|
|
|
сти |
а1 |
|
0 |
5 |
|
10 |
10 |
|
0 |
25 |
25 |
1 |
а2 |
|
0 |
0 |
|
0 |
0 |
|
15 |
15 |
15 |
0 |
а3 |
|
15 |
0 |
|
0 |
0 |
|
5 |
20 |
20 |
0,75 |
Объем |
|
15 |
5 |
|
10 |
10 |
|
20 |
Итого |
60 |
|
доставки |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Потребность |
|
15 |
5 |
|
10 |
10 |
|
|
40 |
|
|
|
|
Целевая функция (минимум) |
|
895 |
|
||||||
152
Таблица 3.12
|
|
|
Потребители |
|
Дос- |
Мощ- |
Коэффи- |
|||
Поставщики |
|
|
|
циент |
||||||
|
|
|
|
|
|
|
тавле- |
|||
|
|
|
|
|
|
Фик- |
ность |
интен- |
||
|
b1 |
b2 |
|
b3 |
b4 |
|
но |
|||
|
|
|
тивный |
|
сивности |
|||||
а1 |
0 |
5 |
|
10 |
10 |
|
0 |
25 |
25 |
1 |
а2 |
0 |
0 |
|
0 |
0 |
|
15 |
15 |
15 |
0 |
а3 |
15 |
0 |
|
0 |
0 |
|
0 |
15 |
15 |
1 |
Объем |
15 |
5 |
|
10 |
10 |
|
15 |
Итого |
55 |
|
доставки |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Потребность |
15 |
5 |
|
10 |
10 |
|
|
40 |
|
|
|
Целевая функция (минимум) |
|
910 |
|
||||||
На четвертой итерации коэффициенты равны либо 0, либо 1, полученооптимальноецелочисленноерешениепоставленнойзадачи.
Таким образом, можно сделать вывод, что в пункте а1 необходимо расширить производство и выбрать вариант модернизации
смощностью 25 т.
Впункте а2 необходимо ликвидировать предприятие, так как в силу затрат на производство и транспортировку продукция этого предприятии невыгодна для реальных потребителей и вся уходит фиктивному потребителю.
Впункте а3 необходимо строить новое предприятие с мощностью 15 т.
Кроме того, решение задачи дает оптимальный вариант закре-
пления поставщиков и потребителей. Предприятие а1 должно поставлять продукцию потребителям b1, b2, b3, а вновь созданное предприятие а3 – потребителю b1.
Оптимальное решение задачи развития и размещения производства носит рекомендательный характер и дает необходимую информацию для окончательных решений.
3.7.Оптимальные смеси
Вданном подразделе показаны возможности использования модели линейного программирования для решения задач оптимального смешивания. Модели оптимального смешивания имеют
153
много общего с моделями оптимального планирования производства. В то же время существуют и некоторые особенности.
Задачи о смесях – значимые прикладные оптимизационные задачи. Такие задачи возникают при выборе наилучшего способа смешивания исходных ингредиентов для получения смеси с заданными свойствами. Смесь должна иметь требуемые свойства, которые определяются количеством компонентов, входящих в состав исходных ингредиентов. Как правило, известны стоимостные характеристики ингредиентов, а искомую смесь требуется получить с наименьшими затратами. Для многопродуктовых задач, в которых требуется получить несколько смесей, характерным является критерий максимизации прибыли.
Задачи оптимального смешивания встречаются во многих отраслях промышленности (металлургия, парфюмерия, пищевая промышленность, фармакология, сельское хозяйство). Примерами задач о смесях могут служить определение кормового рациона скота на животноводческих фермах, составление рецептуры шихты на металлургическом производстве и т.п.
Задача о рационе – это задача, в которой дано определенное количество компонентов, из которых в соответствующих пропорциях создается смесь. Например, определяется состав металлического сплава, бензина или краски, рацион для питания определенной категории людей или животных.
Задача про смесь (рацион) используется также в химической, нефтехимической отраслях, когда нужно создать смеси, качество которых соответствует определенным требованиям.
Моделирование
Рассмотрим однопродуктовые модели оптимального смешивания.
Введем обозначения:
–п – количество исходных ингредиентов;
–т – количество компонентов в смеси;
–хj – количество j-го ингредиента, входящего в смесь;
154
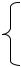
–аij – количество i-го компонента в единице j-го ингредиента (доля i-го компонента в j-м ингредиенте);
–сj – стоимость единицы j-го ингредиента;
–bi – допустимое количество i-го компонента в смеси (минимально допустимая доля i-го компонента в смеси).
Математическая модель задачи примет следующий вид. Целевая функция
n |
|
|
z cj xj min. |
(3.28) |
|
j 1 |
|
|
Система ограничений: |
|
|
n |
|
|
aij xj bi |
(i 1, ..., m), |
(3.29) |
j 1 |
|
|
xij ≥ 0 (j = 1, ..., n). |
(3.30) |
|
(3.28) – целевая функция (минимум затрат на получение смеси). (3.29) – группа ограничений, определяющих содержание ком-
понентов в смеси.
(3.30) – ограничения на неотрицательность переменных.
В задаче могут присутствовать также ограничения на общий объем смеси и ограничения на количество используемых ингредиентов.
Введем дополнительные обозначения:
–w – количество условий, отражающих содержание j-го ингредиента в смеси;
–хj – количество j-го ингредиента, входящего в смесь;
–drj – коэффициент, отражающий r-е условие на содержание j-го ингредиента в смеси.
Математическая модель задачи примет следующий вид. Целевая функция
n |
|
z cj xj min. |
(3.31) |
j 1
155

Система ограничений:
|
n |
|
|
(aij bi )xj 0 (i 1, ..., m), |
(3.32) |
|
j 1 |
|
|
n |
|
|
drj xj 0 (r 1, ..., n), |
(3.33) |
|
j 1 |
|
|
n |
|
|
xj 1 (i 1, ..., m), |
(3.34) |
|
j 1 |
|
|
xij ≥ 0 (j = 1, ..., n). |
(3.35) |
(3.31) – целевая функция (минимум затрат на получение смеси). |
||
(3.32) |
– группа ограничений, определяющих содержание ком- |
|
понентов в смеси. |
|
|
(3.33) |
– группа ограничений на содержание |
ингредиентов |
в смеси. |
|
|
(3.34) |
– ограничение на количество смеси. |
|
(3.35) |
– ограничения на неотрицательность переменных. |
|
Ограничения (3.32) и (3.33) отличают задачу смешения от задачи оптимального планирования производства. Заметим, что зна-
чения правых частей этих ограничений равны нулю. Вектор x* с компонентами, являющийся решением этой оптимизационной задачи, называют рецептом приготовления смеси или рецептом смешения.
Пример решения задачи в Microsoft Excel
Постановка задачи
Предприятие производит бензин. В бензине А-76 октановое число должно быть не ниже 76, а содержание серы не более 0,3 %. Используются 4 ингредиента (1, 2, 3, 4). Данные об используемых ингредиентах представлены в табл. 3.13.
156
|
|
|
Таблица 3.13 |
|
|
|
|
|
|
Показатель, |
|
Ингредиенты бензина |
|
|
единица измерения |
1 |
2 |
3 |
4 |
Октановое число |
68 |
72 |
80 |
9 |
Содержание серы, % |
0,35 |
0,35 |
0,3 |
0,2 |
Ресурсы, т |
700 |
600 |
500 |
300 |
Себестоимость, руб. |
40 |
45 |
60 |
90 |
Требуется определить, сколько тонн каждого ингредиента необходимо для получения 1000 т бензина А-76, чтобы при этом себестоимость бензина была минимальной.
Моделирование
Обозначим переменные величины:
–х1 – количество ингредиента 1,
–х2 – количество ингредиента 2,
–х3 – количество ингредиента 3,
–х4 – количество ингредиента 4. Целевая функция
z = 40х1 + 45х2 + 60х3 + 90х4 → min.
Система ограничений
68x1 72x2 80x3 90x4 76 1000,
0, 35x1 0, 35x2 0, 3x3 0, 2x4 0, 3 1000,x1 x2 x3 x4 1000,
x1 700,x2 600,x3 500,x4 300,
x1, x2, x3, x4 ≥ 0.
Решение
Введем исходные данные и таблицу с изменяемыми ячейками в Excel (рис. 3.31).
157
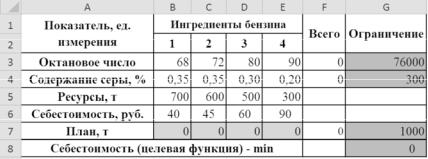
Рис. 3.31
Ячейки B7:E7 предназначены для значений переменных.
G8 – целевая ячейка, в которой будет размещена формула целевой функции.
Вячейку G8 запишем формулу для целевой функции
=СУММПРОИЗВ(B6:E6;B7:E7).
Диапазоны ячеек F3:F7 и G3:G7 содержат ограничения, учитывающие условия состава бензина и объема производства.
Вячейки F3, F4, F7 запишем формулы
=СУММПРОИЗВ(B3:E3;B7:E7), =СУММПРОИЗВ(B4:E4; B7:E7), =СУММ(B7:E7) соответственно.
Для поиска оптимального набора значений параметров смеси бензина, который соответствует минимальному значению целевой функции, воспользуемся надстройкой Поиск решения. Заполним диалоговое окно надстройки (рис. 3.32):
1. ВполеОптимизировать целевуюячейкувведемадресЦФ G8. 2. Ниже выберем параметр Минимум.
3. В поле Изменяя ячейки переменных введем диапазон ячеек
сискомыми переменными B7:E7.
4.Установим флажок Сделать переменные без ограничений неотрицательными и выберем параметр Поиск решения линейных задач симплекс-методом.
5.Щелчком по кнопке Добавить вызовем окно Добавление ограничения. В этом окне введем ссылки на ячейки ограничений,
158

а также выберем оператор ограничений. Для решения данной задачи нам необходимы следующие ограничения:
–B7:E7 ≤B5:E5 – условиеограниченияпоколичествуресурсов;
–F3 ≥ G3 – условие ограничения по октановому числу;
–F4 ≤ G4 – условие ограничения по содержанию серы;
–F7 = G7 – условие ограничения по объему производства.
Рис. 3.32
Нажав кнопку Найти решения, получим результаты решения. В окне Результаты поиска решения выберем отчет и сохраним полученный результат как сценарий (кнопка Сохранить сце-
нарии) с именем Смесь.
159

На рис. 3.33 приведен оптимальный набор ингредиентов, требуемый для производства 1000 т бензина.
Рис. 3.33
Анализ отчетов и выводы по анализу аналогичны тем, что представлены в подразд. 2.6 и 2.7.
3.8.Планирование финансов
Вданном подразделе показаны возможности использования модели линейного программирования для решения некоторых задач планирования финансов. При определенных предположениях становится возможным выбрать такие способы вложения денег под проценты, совокупность которых позволяет минимизировать первоначальный вклад, необходимый для выплаты займа, или максимизировать доход. При решении задач финансового планирования можно учитывать риск и другие факторы, влияющие на выбор способов вложения денег.
Постановка задачи минимизации целевого фонда
Предположим, что в определенные моменты времени необходимо выплачивать известные суммы денег по взятому ранее займу. Чтобы накопить эти суммы, можно заранее создать целевой фонд, а средства из этого фонда использовать для срочных вкладов. Каждый срочный вклад характеризуется моментом времени вложения, сроком погашения и доходностью. Задача состоит в том, чтобы оп-
160
