
Экономические задачи линейного программирования и их решение с испол
..pdf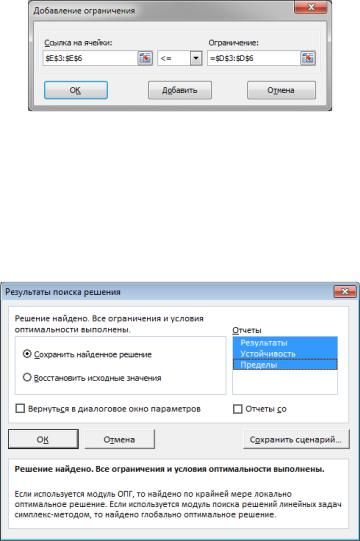
Рис. 2.17
Выполнение процедуры завершается выводом окна Результа-
ты поиска решения.
Решение найдено. Все ограничения и условия оптимальности выполнены. Устанавливаем флажок в положении Сохранить найденное решение. Для анализа результатов решения задачи сформируем отчет, для этого выделим Отчеты (рис. 2.18) и нажмем ОК. Отчет автоматически сформируется на отдельном листе Excel.
Рис. 2.18
В результате поиска решения получаем значения плана производства продукции А = 57,14 шт. и В = 71,43 шт. Максимум выручки при этом составит 2643 руб.
91
Анализ отчетов
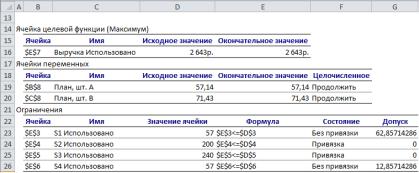
Теперь необходимо проанализировать отчеты, которые мы получили при решении задачи. На рис. 2.19 представлен отчет о результатах.
Рис. 2.19
Проанализировав данные отчета о результатах, получим следующие значения.
Оптимальное значение целевой функции zmax = 2643 руб.
Значения основных переменных прямой задачи:
х1 = 57,14 шт., х2 = 71,43 шт.
Основные переменные не являются целочисленными.
Значения использованных ресурсов:
S1 = 57,14, S2 = 200, S3 = 240, S4 = 57,14.
Значения дополнительных переменных прямой задачи (допуск) –
остаткиресурсов:
x3 = 62,85, x4 = 0, x5 = 0, x6 = 12,86.
На рис. 2.20 представлен отчет об устойчивости. Проанализируем данные отчета об устойчивости. Приведенная стоимость – это значения дополнительных пе-
ременных двойственной задачи; они соответствуют основным переменным прямой задачи и оценивают тот или иной вариант плана.
92
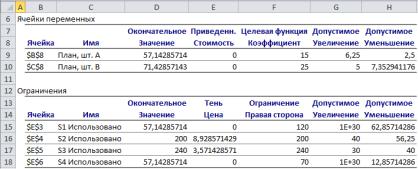
Рис. 2.20
А соответствует приведенная стоимость, равная 0. В соответствует приведенная стоимость, равная 0. Приведенная стоимость равна 0, следовательно, изделия А и В производить выгодно, они вошли в оптимальный план.
Значения коэффициентов эффективности целевой функции и их диапазон:
15 2,5 (c1 15) 15 6, 25, 25 7,35 (c1 25) 25 5.
Это означает, что изменение коэффициентов целевой функции в данных пределах не повлияет на оптимальный план производства (т.е. цены на продукцию А и В могут варьироваться в этих пределах).
Значения основных переменных двойственной задачи (теневая цена) – двойственная оценка ресурсов:
y1 = 0, y2 = 8,93, y3 = 3,57, y4 = 0.
Оценки единицы ресурсов S1 и S4 равны 0, так как эти виды ресурсов в избытке. Дефицитными ресурсами являются ресурсы S2 и S3, оценки которых равны соответственно 8,93 и 3,57. Это означает, что дополнительная единица ресурса S2 может дать увеличение выручки на 8,93 руб., а дополнительная единица ресурса S3 может дать увеличение выручки на 3,57 руб. Таким образом, самым эффективным ресурсом является S2, поскольку его двойственная оценка максимальная. При изменении запасов ресурсов S2 и S3 на единицу выручка увеличится на 8,93 + 3,57 = 12,5 руб.
93
Диапазон устойчивости двойственных оценок ресурсов:
120 62,86 (S1 120) 120 ,
200 56, 25 (S2 200) 200 40, 240 40 (S3 240) 240 30,
70 12,86 (S4 70) 70 .
Таким образом, изменение количества запасов ресурсов в данных пределах не повлияет на значения двойственных оценок, а следовательно, и на эффективность дополнительной единицы соответствующего ресурса.
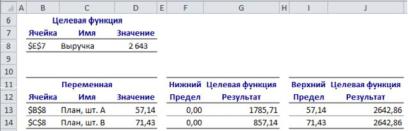
На рис. 2.21 представлен отчет о пределах.
Рис. 2.21
Проанализировав данные отчета о пределах, сделаем вывод,
что при А = 57,14 и В = 0 получим z = 857,14; при А = 0 и В = 71,43 получим z = 1785,71.
2.7.Пример оформления отчета
орешении задачи
После того как задача решена, необходимо составить отчет о решении данной задачи. Приведем пример оформления отчета задачи, решенной в подразд. 2.6.
Сначала необходимо указать Ф.И.О., группу студента и наименование работы, затем переписать задание, составить математические модели прямой и двойственной задач и решить их. После этого выписать значения, полученные при решении задачи, и сформулировать вывод.
94
Ф.И.О., группа
Решение задач линейного программирования
Постановка задачи
Фирма производит два вида продукции – А и В – по определенной цене. На их производство требуется четыре вида ресурсов: S1, S2, S3, S4, которые есть в наличии на фирме в определенном количестве. Нормы расхода ресурсов на изготовление единицы данного вида продукции, цена, получаемая от реализации единицы продукции, а также запасы ресурсов указаны в табл. 1.
|
|
|
Таблица 1 |
|
|
|
|
|
|
Вид |
Норма расхода ресурса |
Запас |
||
на единицу продукции, кг |
||||
ресурса |
ресурса, кг |
|||
А |
В |
|||
|
|
|||
S1 |
0,5 |
0,4 |
120 |
|
S2 |
1,0 |
2,0 |
200 |
|
S3 |
1,7 |
2,0 |
240 |
|
S4 |
0,5 |
0,4 |
70 |
|
Цена, руб. |
15 |
25 |
|
|
Определить объем производства продукции А и В с целью получения максимальной выручки при ограниченном количестве сырья и существующих нормах.
Моделирование
Пусть х1 – количество выпускаемой продукции А (шт.); х2 – количество выпускаемой продукции В (шт.).
Тогда математическая модель прямой задачи примет вид: z = 15x1 + 25x2 → max,
0,5x1 0, 4x2 120,x1 2x2 200,1,7x1 2x2 240,0,5x1 0, 4x2 70,
х1, х2 ≥ 0.
95
А математическая модель двойственной задачи примет вид: f = 120y1 + 200y2 + 240y3 + 70y4 → min,
0,5y1 y2 1, 7 y3 0,5y4 15,0, 4y1 2y2 2 y3 0, 4y4 25,
y1, y2, y3, y4 ≥ 0.
Решение
Оптимальное значение целевой функции zmax = 2643 руб.
Значения основных переменных прямой задачи: x1 = 57,14 шт., x2 = 71,43 шт.
Значения дополнительных переменных прямой задачи: x3 = 62,85, x4 = 0, x5 = 0, x6 = 12,86.
Значения основных переменных двойственной задачи: y1 = 0, y2 = 8,93, y3 = 3,57, y4 = 0.
Диапазон устойчивости двойственных оценок ресурсов:
57,14 ≤ S1 ≤ ∞, 143,75 ≤ S2 ≤ 240,
200 ≤ S3 ≤ 270, 57,14 ≤ S4 ≤ ∞.
Значения дополнительных переменных двойственной задачи (для соответствующих видов продукции):
–А соответствует приведенная стоимость, равная 0.
–В соответствует приведенная стоимость, равная 0.
Значения коэффициентов эффективности целевой функции и их диапазон: 12,5 ≤ с1 = 15 ≤ 21,25, 17,65 ≤ с2 = 25 ≤ 30.
Выводы
Выпуск продукции
Максимум выручки составит 2643 руб. Для достижения максимальной выручки необходимо производить продукцию А в количестве 57,14 шт. и продукцию B в количестве 71,43 шт.
96
Использование ресурсов
Ресурсы вида S2 и S3 использованы полностью в объемах соответственно 200 и 240 кг. Ресурс вида S1 использован не полностью, остаток ресурса составит 62,85 кг. Ресурс вида S4 использован не полностью, остаток ресурса составит 12,86 кг.
Оценки ресурсов
Оценки единицы ресурсов S1 и S4 равны 0, так как эти виды ресурсов в избытке. Дефицитными ресурсами являются ресурсы S2 и S3, оценки которых равны соответственно 8,93 и 3,57. Это означает, что дополнительная единица ресурса S2 может дать увеличение выручки на 8,93 руб., а дополнительная единица ресурса S3 может дать увеличение выручки на 3,57 руб. Таким образом, если взять не 200, а 201 кг ресурса S2 и оптимально решить задачу, то целевая функция 2643 + 8,93 = 2651,93 руб. Данное утверждение справедливо для всех оценок в пределах их устойчивости. Например, для S2 можно увеличить объем на 40 кг и иметь увеличение выручки на величину 8,93 · 40 = 357,2 руб.
Самым эффективным ресурсом является S2, так как его двойственная оценка максимальная.
Оценки вариантов плана
Продукцию вида А и В выгодно производить, так как соответствующие дополнительные переменные двойственной задачи равны нулю. Эти изделия вошли в оптимальный план. Чем меньше дополнительная переменная двойственной задачи, тем выгоднее производить соответствующий вид продукции.
Оценка коэффициентов эффективности
Объем выручки не изменится, если цены на продукцию будут находиться в следующих пределах:
12,5 руб. ≤ Цена продукции А ≤ 21,25 руб., 17,65 руб. ≤ Цена продукции В ≤ 30 руб.
97
ГЛАВА 3. ПРИМЕНЕНИЕ НАДСТРОЙКИ «ПОИСК РЕШЕНИЯ» ДЛЯ РЕШЕНИЯ ТИПОВЫХ ЭКОНОМИЧЕСКИХ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
В данном разделе рассмотрены типовые экономические задачи линейного программирования, а также способ их решения с помощью надстройки Поиск решения.
3.1. Определение оптимального ассортимента
Задача определения оптимального ассортимента позволяет спланировать производство из имеющегося ассортимента таких видов продукции и в таком количестве, которое дает максимальный эффект при заданных ограниченных ресурсах.
Постановка задачи
Суть задачи заключается в определении плана производства одного или нескольких видов продукции, который обеспечивает наиболее рациональное использование имеющихся материальных, финансовых и других видов ресурсов. Такой план должен быть оптимальным с точки зрения выбранного критерия – максимума прибыли, минимума затрат на производство и т.д.
Имеется m видов ресурсов в количестве b1, b2, ..., bт, которые могут быть использованы при производстве n видов продукции. Известны нормы расхода i-го вида ресурса на производство единицы j-го вида продукции (aij). Эффективность выпуска единицы j-й продукции характеризуется коэффициентом cj. Следует определить план выпуска изделий (оптимальный ассортимент), при котором суммарный показатель эффективности принимает наибольшее (наименьшее) значение и расход ресурсов каждого вида не превышает имеющегося объема.
Моделирование
Обозначим оптимальный план выпуска каждого вида продукции соответственно через x1, x2, ..., xn. Тогда математическая модель задачи примет вид:
98
z = c1x1 + c2x2 +…+ cnxn → max, |
|
(3.1) |
||||||||||||
a |
|
x |
a |
|
x |
|
... a |
x |
|
b , |
|
|
||
11 |
1 |
12 |
|
2 |
|
1n n |
|
1 |
|
|
||||
a21x1 |
a22 x2 |
... a2n xn |
b2 , |
|
(3.2) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... ... ... ... ... ... ... ... ... ..., |
|
|||||||||||||
a |
|
x |
a |
m2 |
x |
2 |
... a |
mn |
x |
n |
b |
, |
|
|
|
m1 1 |
|
|
|
|
m |
|
|
||||||
|
|
|
xj ≥ 0, j = 1, 2, ..., n, |
|
|
(3.3) |
||||||||
где (3.1) – целевая функция (максимум); (3.2) – система специальных ограничений на объем фактически
имеющихся ресурсов; (3.3) – система общих ограничений (на неотрицательность пе-
ременных).
Задача (3.1)–(3.3) является задачей линейного программирования (ЗЛП) в стандартной форме на максимум.
Примечание: кроме указанных ограничений по ресурсам (3.2) в условие задачи, а следовательно, и в ее математическую модель могут вводиться дополнительные ограничения на планируемый выпуск продукции (ограничения по ассортименту, условия комплектности и т.д.). Например, дополнительные условия, чтобы изделий третьего вида производилось не меньше k штук, а количество изделий первого и второго вида относилось друг к другу как 1:2, запишутся в виде:
x3 k,
2x1 x2 .
С каждой ЗЛП связывают другую ЗЛП, которая записывается по определенным правилам и называется двойственной ЗЛП.
Двойственной по отношению к ЗЛП (3.1)–(3.3) является задача
g = b1y1+ b2y2 +…+ bmym → min, |
(3.4) |
|||||||||||||||
a |
y |
a |
|
y |
|
|
... a |
m1 |
y |
m |
c , |
|
|
|||
11 |
1 |
|
21 |
|
2 |
|
|
|
1 |
|
|
|||||
a12 y1 |
a22 y2 |
... am2 ym |
c2 |
, |
(3.5) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... ... ... ... ... ... ... ... ... ..., |
|
|||||||||||||||
a |
y |
a |
2n |
y |
2 |
... a |
mn |
y |
m |
c |
, |
|
||||
1n |
1 |
|
|
|
|
|
|
|
n |
|
|
|||||
99

yi ≥ 0, i = 1, 2, ..., m. |
(3.6) |
Соответственно, двойственной по отношению к ЗЛП (3.4)– (3.6) является задача (3.1)–(3.3). Каждой переменной (специальному ограничению) исходной задачи соответствует специальное ограничение (переменная) двойственной задачи. Если исходная ЗЛП имеет решение, то имеет решение и двойственная по отношению к ней задача, при этом значения целевых функций для соответствующих оптимальных решений равны.
Перменная yi* оптимального решения двойственной задачи (3.4)–(3.6) называется двойственной оценкой ограничения исходной ЗЛП.
Пусть |
|
n |
|
, где хj |
– переменная допустимого |
max |
c j x j |
||||
|
|
j 1 |
|
|
|
решения задачи (3.1)–(3.3). Тогда при выполнении условий невырожденности оптимального решения имеют место следующие соотношения:
d yi* , i 1, , m. dbi
Изменим значение правой части bi одного основного ограничения исходной ЗЛП. Пусть bi′ – минимальное значение правой части основного ограничения, при котором решение у* двойственной задачи не изменится. Тогда величину bi′ называют нижней границей устойчивости по правой части ограничения. Пусть bi′′ – максимальное значение правой части основного ограничения, при котором решение y* двойственной задачи не изменится. Тогда величину bi′′ называют верхней границей устойчивости по правой части ограничения.
Изменим значение одного коэффициента сj целевой функции исходной ЗЛП.
Пусть сj′ – минимальное значение коэффициента целевой функции, при котором оптимальное решение x* исходной задачи не изменится. Тогда величину сj′ называют нижней границей ус-
100
