
Оптимальное проектирование конструкций
..pdf
Запишем необходимые условия оптимальности:
|
∂ V1 |
= |
F1l sin α |
+ λ |
|
P cos α |
|
− λ |
|
|
P |
|
= 0; |
∂ V1 |
= |
|
l |
− λ |
[σ ] = 0; |
|||||||||
|
∂ α |
|
1 sin2 α |
|
2 sin2 |
α |
∂ F1 |
|
cos α |
|||||||||||||||||||
|
|
cos2 α |
|
|
|
|
|
|
|
|
|
|
1 |
|||||||||||||||
∂ V1 |
= l − λ |
2 |
[σ ] |
= 0; |
|
|
∂ V1 |
|
= |
|
P |
|
|
−[σ |
]F = 0; |
|
∂ V1 |
|
= Pctgα −[σ ]F = 0. |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||
∂ F2 |
|
|
|
|
|
|
|
∂ λ 1 |
|
|
sin α |
|
|
|
1 |
|
∂ λ |
2 |
|
|
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Выражая из второго и третьего уравнений λ1 и λ2, а из двух послед-
них – F1 и F2 и подставляя эти соотношения в первое уравнение, получим уравнение для α:
|
|
2 |
1 |
|
|
|
|
|
|
|
|
||||
|
|
− |
|
|
+ |
|
= 0. |
|
|
|
|
|
|||
|
|
sin2 α |
cos2 α |
|
|
|
|
|
|||||||
Отсюда |
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
tgα = 2; |
F |
=1,226 |
; |
F = |
0,707 |
P |
; |
V |
= 2,83 |
Pl |
. |
||||
|
|
|
|||||||||||||
|
1 |
[σ ] |
2 |
|
[σ ] |
|
min |
[σ ] |
|||||||
|
|
|
|
|
|
|
|||||||||
Задача легко решалась бы и методом исключения, однако метод множителей Лагранжа необходим, если нельзя выразить в явном виде одно из ограничений через другое.
4.1.2. Общий случай ограничений
Выведем необходимые условия для случая только ограничений не-
равенств, т.е. когда требуется решить задачу |
минимизации функции |
f (x) min ( x = (x1, x2 , ..., xn ) ) при условии g j (x) ≥ |
0, j =1, ..., m. |
Ограничения в форме неравенства всегда можно перевести в ограни- чения-равенства, для чего достаточно вычесть из каждого ограничения не-
отрицательную переменную u2j (u2j ≥ 0 всегда): g j (x) − u2j = 0.
Это позволяет перейти к задаче с ограничениями-равенствами, а затем составить функцию Лагранжа
|
m |
2j ] |
F (x, λ , u) = |
f (x) + ∑ λ j [g j (x) − u |
|
|
i =1 |
|
и записать необходимые условия оптимальности
71
|
|
∂ F |
|
∂ f |
m |
|
∂ g j |
|
|
|
|
|
= |
|
+ ∑ λ j |
|
|
|
= 0; |
|
|
∂ xi |
|
|
∂ xi |
||||
|
|
|
∂ xi j =1 |
|
|
||||
∂ F |
= g j (x) − u2j = 0; |
∂ F |
= 2λ ju j = 0. |
||||||
|
|
||||||||
∂ λ j |
|
|
|
∂ u j |
|
||||
Умножив последнее из уравнений на ui , получим
2λ ju 2j = 0.
Из полученного уравнения следует, что оно выполняется, если либо λ j = 0 (это означает, что ограничение неактивно и не влияет на положение
минимума, поэтому его просто можно не учитывать), либо если u2j = 0 . Из
последнего соотношения видно, что на положение минимума влияют только активные ограничения-неравенства (переходящие в равенство). Однако заранее неизвестно, какие из ограничений-неравенств активны.
Кун и Таккер построили необходимые и достаточные условия оптимальности для задач нелинейного программирования: минимизировать
f (x), |
x = (x1, x2 , ..., xn ) |
при ограничениях |
|
h j (x) = 0, |
j = 1, 2, ..., k; |
g j (x) ≥ 0, |
j = k +1, ..., m. |
Необходимые условия оптимальности сформулированы в форме тео-
ремы.
Теорема. Если х* допустимое оптимальное решение задачи, в которой f , g, h – дифференцируемые функции, и если градиенты h j (x* ) и
g j (x* ) для всех j , при которых g j (x* ) = 0 (или для всех активных огра-
ничений), линейно-независимы, то существуют такие векторы u*, v* , которые удовлетворяют условиям
∂ f |
|
m |
|
∂ g j (x) |
k |
|
∂ h j (x) |
|
|
|
− |
∑ |
u j |
|
− ∑ v j |
|
|
= 0, |
i = 1, ..., n; |
∂ xi |
∂ xi |
|
∂ xi |
||||||
|
j =1+ k |
|
j =1 |
|
|
|
|||
|
|
|
u j g j (x) = 0, |
j = 1 + k, ..., m; |
|
||||
|
|
|
|
u j ≥ 0; g j (x) ≥ 0; |
|
||||
|
|
|
|
h j (x) = 0; |
|
j = 1, ..., k. |
|
||
72
Условие линейной независимости градиентов представляет собой некоторое условие регулярности градиентов допустимой области, которое почти всегда встречается в практических задачах. Проверить условия ли-
нейной независимости можно, если известно х* . Однако в следующих случаях условия линейной независимости выполняются всегда:
1)ограничения в виде равенств и неравенств – линейные функции;
2)все ограничения в виде неравенств – вогнутые функции, а ограни- чения-равенства – линейные функции и существует хотя бы одна допустимая точка, которая расположена во внутренней части области, определяемой ограничениями-неравенствами.
Обратим внимание, что на переменные u j наложены условия неот-
рицательности, в то время как на v j ограничения на знак отсутствуют. Требование u j g j (x) = 0 называется условием дополняющей жесткости.
Условия Куна–Такера совпадают с условиями Лагранжа для задач с ограничениями-равенствами.
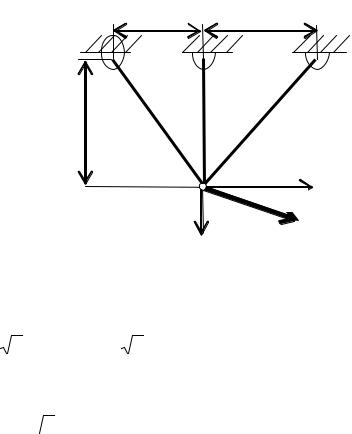
Пример 4.5. Оптимизация трехстержневой фермы
чи – в примере 1.2). |
|
|
|
|
|
|
|
||||
Целью проектирования являет- |
|
|
|
|
|
|
|
||||
ся выбор площадей поперечных се |
|
|
|
L1 |
|
||||||
|
|
|
|
||||||||
- |
|
|
|
|
|
|
1 |
|
|
||
чений отдельных стержней s1, s2, s3 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|||||
(переменные проектирования или |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||||
оптимизации) при условии, что фер- |
|
|
|
|
|
|
|
||||
ма по возможности легкая и удовле- |
|
|
|
|
|
|
|
||||
творяются ограничения на напряже- |
|
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
||||
ния. |
|
L |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Будем полагать, что материал всех стержней одинаковый, однородный и упругий, размер сечения неизменен по всей длине.
(постановка зада-
L22
2
3
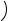 αH xх
αH xх
yу PР
Положим для простоты L1 = |
|
= L2 = L, тогда критерий качества – |
Рис. 4.7 |
вес – можно записать в виде |
|
f (s1, s2 ) = ρ g(s1 2L + s2 L + s3L |
2) min . |
Если, кроме того, ферма симметричная ( s1 = s3 ), то
f (s1, s2 ) = ρ g(2 2s1 + s2 )L min
2s1 + s2 )L min
73
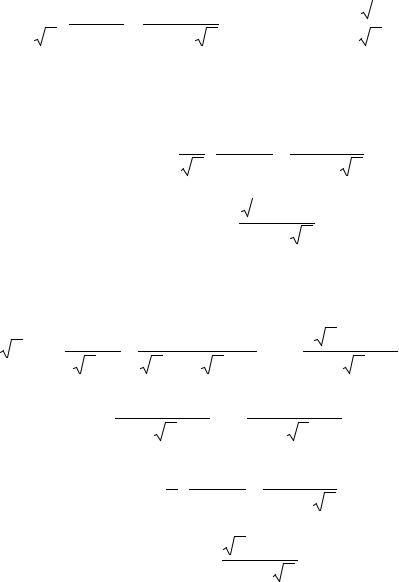
при прочностных ограничениях
1 |
|
P cos α |
|
P sin α |
|
|
|
|
P sin α |
|
|
|
|
|
|
|
0 |
|
2 |
|
|
0 |
|||||||
|
|
|
+ |
|
|
≤ σ |
|
и |
|
|
|
|
≤ |
σ . |
|
|
|
|
|
|
|
|
|||||||
|
|
s1 |
s1 + s2 |
|
|
s1 + s2 |
2 |
|
||||||
2 |
|
2 |
|
|
|
|
|
|
||||||
Добавим еще условия невырождения фермы: s1 > 0 и |
s2 > 0 , и пере- |
|||||||||||||||||||
пишем прочностные ограничения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
0 |
|
1 |
P cos α |
|
P sin α |
|
|
|
|
|
|
|||||
g1(s1, s2 ) = σ − |
|
|
|
|
|
|
|
+ |
|
|
|
|
|
|
|
|||||
|
|
s1 |
|
|
s1 + s2 |
≥ 0; |
|
|
|
|||||||||||
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
P sin α ≥ 0. |
|
|
|
|
|
|
||||
|
g |
2 |
(s |
, s |
2 |
) = σ 0 − |
|
|
2 |
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
s1 + s2 |
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Запишем теперь условия Куна–Таккера (без учета коэффициента ρ g |
||||||||||||||||||||
в функции качества): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P cos α |
+ |
|
P sin α |
|
|
|
|
− u |
2P sin α |
|
− u |
|
= 0; (4.10) |
||||||
2 2 − u |
|
|
2 |
|
2 |
3 |
||||||||||||||
1 |
2 |
|
2(s1 + 2s2 ) |
|
|
2 |
2s2 ) |
|
|
|
||||||||||
|
2s1 |
|
|
|
|
|
(s1 + |
|
|
|
|
|
||||||||
1 − u1 (s |
P sin α |
|
|
|
|
2P sin α |
)2 − u4 = 0; |
|
||||||
+ |
|
2s |
2 |
)2 − u2 (s + |
2s |
2 |
(4.11) |
|||||||
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
||
|
0 |
|
1 |
P cos α |
|
P sin α |
|
|
||||||
u1 σ |
|
− |
|
|
|
|
+ |
|
|
|
|
|
(4.12) |
|
|
|
|
s1 |
|
|
+ s2 |
|
= 0; |
||||||
|
|
|
2 |
|
|
s1 |
|
2 |
|
|||||
|
|
|
|
|
0 |
|
2P sin α |
|
|
|
|
|||
|
|
|
|
σ |
|
− |
|
|
|
|
|
|
|
(4.13) |
|
|
u2 |
|
|
+ s2 |
|
|
= 0; |
||||||
|
|
|
|
|
|
|
s1 |
|
2 |
|
|
|
||
|
|
|
|
|
|
u3s1 = 0; |
|
|
|
|
|
(4.14) |
||
|
|
|
|
|
|
u4s2 = 0. |
|
|
|
|
(4.15) |
|||
Но s1 ≠ 0 и s2 ≠ 0 , поэтому из (4.14) и (4.15) следует, что u3 = u4 = 0 . |
||||||||||||||
В итоге получили четыре уравнения с четырьмя неизвестными. |
|
|||||||||||||
Рассмотрим возможные варианты решений: |
|
|||||||||||||
1. Решение u1 = u2 = 0 невозможно, |
|
ибо тогда уравнения (4.10) и |
||||||||||||
(4.11) не совместны (на практике это решение означает, что стержни работают не на пределе, ограничения – не активны).
74

2. Если u1 = 0, u2 ≠ 0 (средний стержень работает на пределе своих
прочностных возможностей), то из (4.13) следует, что |
|
2 |
P sin α |
= σ 0 , но |
|||
s |
|
|
|
||||
|
|
+ s |
2 |
2 |
|
||
1 |
|
|
|
|
|||
тогда уравнения (4.10) и (4.11) не совместны. Следовательно, такое решение также невозможно.
|
3. |
Если |
|
u1 ≠ 0, u2 = 0 (два крайних стержня работают на пределе |
|
своих |
прочностных возможностей), то из уравнения (4.11) получаем |
||||
u = (s + |
2s |
2 |
)2 |
/ P sin α . Подставляя их в уравнение (4.10) и учитывая |
|
1 |
1 |
|
|
|
|
уравнение (4.12), получаем два уравнения относительно двух неизвестных:
|
(s + 2s |
2 |
)2 |
|
P cos α |
P sin α |
|
|
|
||
2 2 − |
1 |
|
|
|
2 + |
|
|
2 |
|
= 0; |
|
P sin |
α |
|
|
|
2(s1 + |
2s2 ) |
|
||||
|
|
|
|
2s1 |
|
|
|
||||
0 |
1 |
|
P cos α |
|
P sin α |
|
|
σ − |
|
|
|
+ |
|
|
= 0. |
|
|
s1 |
s1 + s2 |
|
|||
|
2 |
|
2 |
|
|||
Решая эту систему и накладывая требование неотрицательности на значение площадей, получаем, что решение возможно, если 18,40 ≤ α ≤ 71,60.
4. Если u1 ≠ |
0, u2 ≠ |
0 (все стержни работают на пределе своих проч- |
||||||||||
ностных возможностей), то из соотношений (4.12) и (4.13) следует |
||||||||||||
|
|
0 |
|
1 |
P cos α |
|
|
P sin α |
|
|||
|
σ |
|
− |
|
|
|
|
|
+ |
|
= 0, |
|
|
|
|
|
s1 |
|
|||||||
|
|
|
|
2 |
|
|
s1s2 2 |
|
||||
|
|
|
|
|
|
|
P sin α = 0. |
|
||||
|
|
|
|
σ 0 − |
|
2 |
|
|||||
|
|
|
|
|
|
s1 + s2 |
|
2 |
|
|||
Решим эти уравнения: |
|
|
|
|
|
|
|
|
||||
s = |
2P cos α |
/ σ 0 ; |
|
|
|
s |
2 |
= P(sin α |
− cos α ) / σ 0. |
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Так как s2 > 0, то это возможно, если sin α |
> cos α , т.е. если α > 450. |
|||||||||||
Подставим найденные значения в уравнения (4.10) и (4.11) и получим |
||||||||||||
u = 3P cos α |
/(σ 0 )2 ; |
|
|
u |
2 |
= P(sin α − 3cos α ) /(σ 0 )2. |
||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Согласно теореме Куна–Таккера на переменные ui наложено требование неотрицательности, следовательно, найденное решение справедливо только при α ≥ 71,60.
75
Если условия Куна–Таккера выполняются, то нет гарантии, что найдено оптимальное решение нелинейной задачи.
Приведенная ниже теорема устанавливает условия, при выполнении которых найденная точка соответствует оптимальному решению.
Теорема. Если целевая функция f (x) , минимум которой необходимо найти, выпуклая, все ограничения в виде неравенств g j (x) ≥ 0 функции вогнутые, а ограничения в виде равенств h j (x) = 0 линейные функции и
существует решение (x*, u*, v* ), удовлетворяющее условиям Куна– Таккера, то x* – оптимальное решение поставленной задачи.
Пример 4.6. Оптимизация трехстержневой фермы. В предыдущем примере 4.5 было найдено решение этой оптимизационной задачи. Покажем, что при этом выполнены не только необходимые условия, но и достаточные, т.е. найденные решения соответствуют условию минимума веса фермы. Для этого достаточно доказать, что функция f (x) выпуклая, а
функции ограничений вогнутые функции. В нашем примере f (s1, s2 ) = = ρ g(2 2s1 + s2 )L – линейная функция переменных проектирования, сле-
2s1 + s2 )L – линейная функция переменных проектирования, сле-
довательно, она одновременно выпукла и вогнута. Ограничения имеют вид
|
|
|
0 |
|
1 |
P cos α |
|
P sin α |
|
|
|||
g1(s1, s2 ) = σ − |
|
|
|
|
|
+ |
|
|
≥ 0; |
||||
|
|
s1 |
s1 + s2 |
|
|||||||||
|
|
|
|
|
2 |
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
P sin α ≥ 0. |
|
|
|||
g |
2 |
(s |
, s |
2 |
) = σ 0 − |
|
2 |
|
|
||||
|
1 |
|
|
|
s1 + s2 |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||
Умножим ограничения на (–1) и докажем их выпуклость, для чего вычислим матрицу Гессе для каждой из функций:
2P sin α |
1 + (1 + |
2s |
2 |
/ s |
)3 ctgα |
2 |
|||
|
|
|
|
|
1 |
|
|
; |
|
(s1 + 2s2 )3 |
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
2 |
||
|
2P sinα |
|
2 |
|
|
|
|
||
|
|
|
2 |
|
|
||||
|
(s1 + 2s2 )3 |
|
|
|
|
|
|||
|
2 |
|
2 2 |
. |
|
||||
|
|
|
|
|
|
|
|
|
|
Первая матрица определенно-положительная (члены по главной диагонали положительны и все главные миноры также положительны), а вторая матрица положительно полуопределена. Поэтому умноженные на (–1) функции ограничений – выпуклые функции, а исходные функции ограни-
76
чений – вогнутые. В итоге заключаем, что задача имеет абсолютный минимум, так как все необходимые и достаточные условия выполнены.
Задачи для самостоятельного решения
Найти оптимальные решения согласно условиям Куна–Таккера и отобрать те из них, которые удовлетворяют достаточным условиям.
1. Рассмотреть задачу минимизации веса замкнутого стального тонкостенного цилиндрического баллона давления, вмещающего по крайней
мере 0,6 м3 газа при давлении 3 МПа. Окружная деформация не должна превосходить 10–3 и должно выполняться условие прочности.
2. Рассмотреть задачу минимиза- |
|
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
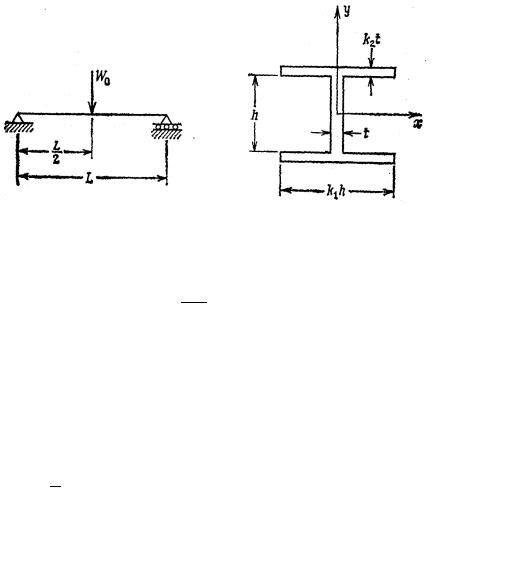
ции веса колонны (рис. 4.8) при ограни- |
|
||||||
|
|
|
|
|
|
|
|
чениях на напряжения и устойчивость, а |
|
|
|
|
|
|
|
также при ограничениях на местное вы- |
|
|
|
|
|
|
|
|
|
|
|
|
R |
||
пучивание. |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
3. Призматическая стальная балка |
|
|
L |
|
|||
с горизонтальной осью проектируется на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
сосредоточенную нагрузку (рис. 4.9). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Балка должна иметь минимальный вес |
|
|
|
|
|
|
|
при ограничениях на изгибающие на- |
|
Рис. 4.8 |
|||||
пряжения в полках и на местную потерю |
|
||||||
|
|
|
|
|
|
|
|
устойчивости полок и стенок. Считать переменные k1, k2 заданными. Момент инерции сечения в предположении t << h можно записать в виде:
I xx = th3 (1 + 6k1k2 ) . 12
R
k2t
W0
h
t x
L
2
L
k2h
Рис. 4.9
При рассмотрении местной потери устойчивости формы выпучивания принять как при потери устойчивости пластины.
77
4.2.Линейное программирование
4.2.1.Постановка задач линейного программирования и графический метод решения
Задачами линейного программирования называются оптимизационные задачи, в которых ограничения (как в виде равенств, так и неравенств) и целевая функция линейны. Методы линейного программирования широко используются для решения различных военных, экономических, промышленных и организационных задач. Главными причинами столь широкого применения этих методов являются доступность математического обеспечения для решения задач большой размерности и возможности анализа решения при вариации исходных данных. Кроме того, линейное программирование можно использовать в задачах нелинейного программирования на этапах линеаризации.
Известно, что в настоящее время около 74 % от общего числа применяемых оптимизационных методов составляют методы линейного программирования. Около четверти машинного времени, затраченного в последние годы на проведение научных исследований, было отведено решению задач линейного программирования и их многочисленных модификаций.
Рассмотрим основные особенности задач линейного программирования на простом примере назначения персонала.
Пример 4.7. В отделе технического контроля некоторой фирмы работают контролеры первого и второго разряда. Норма выработки отдела за 8-часовой рабочий день составляет не менее 1800 изделий. Контролер первого разряда проверяет 25 изделий в час, причем не ошибается в 98 % случаев. Контролер второго разряда проверяет 15 изделий в час, его точность 95 %. Заработная плата контролера первого разряда 4 у.е. в час, второго – 3 у.е., при каждой ошибке фирма несет убыток в 2 у.е. Фирма может использовать не более 8 контролеров первого разряда, и не более 10 – второго. Найти оптимальный состав, при котором затраты были бы минимальны.
Р е ш е н и е . Составим сначала математическую модель: обозначим через х1 число контролеров первого разряда, а через х2 число контролеров второго разряда. Подсчитаем затраты фирмы на работу контролеров первого разряда в день – 8(4 + 2 25 0,02), второго – 8(3 + 2 15 0,05). Общие затраты:
8[(4 + 2 25 0.02) х1 + (3 + 2 15 0.05) х2] → min.
78
Количество проверяемых изделий в день составляет
8(25 х1 + 15 х2) ≥ 1800.
Таким образом, формулировка задачи будет следующей: найти х1 и х2 такие, чтобы
z(x) = 40x1 + 36x2 min
при ограничениях
5x1 + 3x2 ≥ |
45; |
|||
x1 ≥ |
0; |
x1 |
≤ |
8; |
x2 ≥ |
0; |
x2 |
≤ |
10. |
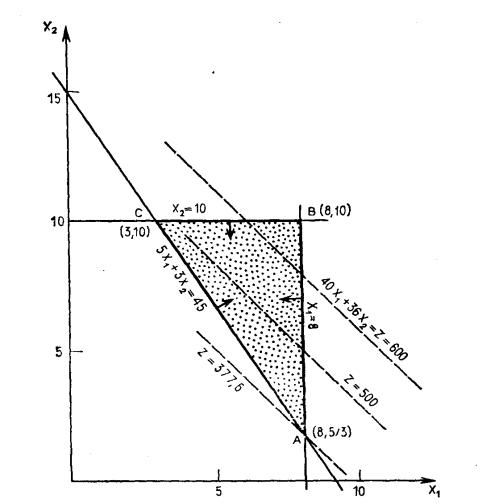
Решим задачу графически (рис. 4.10). На практике графический метод используется редко, так как его можно использовать только для решения задач, размерность которых не более 2, однако в нашем случае этот
Рис. 4.10
79
метод позволяет иллюстрировать некоторые основные понятия линейного программирования.
Решение, удовлетворяющее всем ограничениям, называется допустимым. Множество допустимых решений составляет допустимую область. Лучшее допустимое решение называется оптимальным, значение функции качества при этом называется оптимальным значением задачи линейного программирования.
Для изображения допустимой области следует начертить графики всех ограничений. Все допустимые решения сформулированной задачи
лежат в первом квадранте, ибо xi ≥ 0 . Ограничения x1 ≤ |
8 и x2 ≤ 10 сужа- |
ют эту область до прямоугольника. Учет ограничения |
5x1 + 3x2 ≥ 45 дает |
область допустимых значений в форме треугольника (на рисунке этот треугольник зашрихован). Чтобы определить, какая из областей выше или ниже прямой является допустимой, достаточно рассмотреть любую точку, например, начало координат. Так как в этой точке ограничение не выполняется, то допустимой является заштрихованная область.
Для нахождения точки, в которой z min , нужно зафиксировать значение целевой функции, например, положить z = 600 . Точки, соответствующие этому значению, будут лежать на прямой
z = 40x1 + 36x2 = 600 .
При изменении величины z эта прямая подвергается параллельному переносу. При приближении этой прямой к началу координат значение z уменьшается, следовательно, наименьшим значением z будет такое, при котором эта прямая будет иметь последнюю общую точку с допустимой
областью АВС. Такой точкой является точка А с координатами х1 = 8 и
х2 = 1,6, а наименьшее значение z = 377,6. Это и есть оптимальное решение задачи.
Таким образом, для оптимального режима работы отдела необходимо использовать 8 контролеров первого разряда и 1,6 контролеров второго
разряда. Дробное значение х2 = 1,6 соответствует использованию одного из контролеров второго разряда в течение неполного рабочего дня. Если же это невозможно, то решение обычно округляют, получая приближенное
целочисленное значение х1 = 8 и х2 = 2.
Обратим внимание, что решением задачи являлись вершины допустимой области и полученное решение было единственным.
Однако для некоторых задач линейного программирования может существовать несколько допустимых решений со значениями целевой функции, равными оптимальному значению задачи. В таких случаях все допустимые решения оптимальны и говорят, что задача линейного программирования имеет альтернативные оптимальные решения.
80
