
Оптимальное проектирование конструкций
..pdf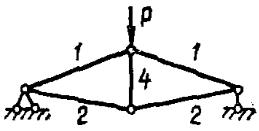
0,634(σ 0 F1 − Y1) + P + σ 0 F4 − Y4 = 0.
Таким образом, задача свелась к нахождению положительных переменных F1, F2 , F3 , F4 , y1, y2 , y3 , y4 , Y1, Y2 , Y3 , Y4 , при которых функция
z= G / γ = 12,64F1 +12,06F2 +12F3 + 2,6F4 min
ивыполняются ограничения (*).
Решая задачу симплекс-методом, получаем
|
|
|
|
|
|
|
|
zmin = 29,9 |
P |
|
|
|
||
|
|
|
|
|
|
|
σ 0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
при F |
= 1,21 |
P |
; |
F = |
1,16 |
P |
; |
F = 0; |
F = 0,232 |
P |
; |
|||
|
|
|
||||||||||||
1 |
|
σ 0 |
|
2 |
|
σ 0 |
3 |
|
4 |
σ 0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Y1 = y2 = y3 = Y4 = 0; |
у1 = 2,42P; Y2 = −7,676P; |
|||||||||||
|
|
|
|
|
|
Y3 = 9,953P; |
у4 = 1,999P. |
|
|
|||||
Равенство |
F3 = 0 |
показывает, |
что |
|
|
|
|
|||||||
для получения оптимальной фермы надо |
|
|
|
|
||||||||||
убрать |
|
стержень |
3. |
|
|
Условия |
|
|
|
|
||||
Y1 = y2 = Y4 = 0 соответствуют тому, |
что |
|
|
|
|
|||||||||
первый и четвертый стержни предельно |
|
|
|
|
||||||||||
сжаты, а второй – предельно растянут. |
|
|
|
|
||||||||||
Оптимальная |
схема |
статически |
|
|
|
|
||||||||
определимой |
|
фермы |
показана |
на |
|
|
|
Рис. 4.16 |
||||||
рис. 4.16. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 4.12. Оптимизация расхода материала конструкций. Фирма выпускает рамные конструкции с преобладающим изгибом (рис. 4.17).
Первая рама выпускается в количестве 10 штук, вторая – в количестве 20 штук, но по условиям унификации ригели и стойки для обеих рам должны быть одинаковыми. Подобрать такие сечения, чтобы вся совокупность элементов обладала минимальной стоимостью, и сравнить полученное решение с результатом оптимального проектирования без учета унификации.
Р е ш е н и е . Решим задачу без учета унификации. Целевые функции для каждой из рам будут иметь вид
91
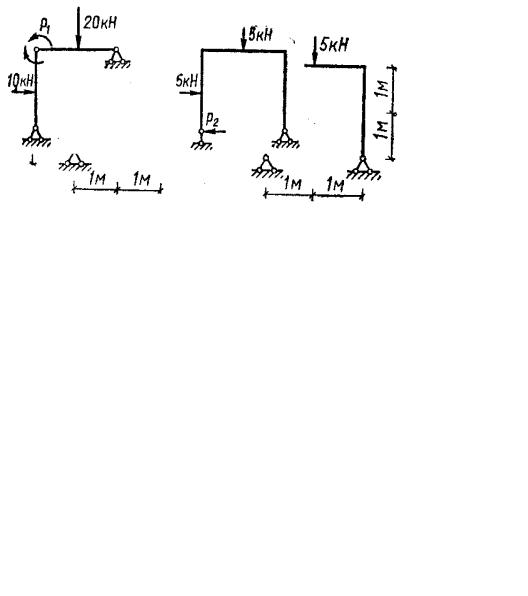
Рис. 4.17
z = M |
1 |
+ M |
1 |
min; |
(4.21) |
1 |
c |
|
p |
|
|
z2 = M c2 + M p2 min, |
(4.22) |
||||
где M p и M с – предельные пластические моменты ригеля и стойки.
Раскрывая статическую неопределенность (рис. 4.18), введем новые переменные р1 и р2 .
Рассмотрим для каждой конструкции опасные сечения и соста-
|
|
|
|
вим условия пластичности: |
|||||||
|
|
|
|
для первой конструкции |
|||||||
|
|
|
|
|
− Мс1 ≤ |
5 − |
р1 |
≤ Мс1; |
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
Рис. 4.18 |
|
|
|
|
− М1 |
≤ |
р ≤ |
М1; |
|||
|
|
|
|
|
с |
|
1 |
с |
|||
− М1 |
≤ р ≤ М1 |
; − М1 ≤ 10 − |
|
р1 |
≤ М1 |
; |
|
|
|||
|
|
|
|
||||||||
р |
1 |
р |
|
р |
2 |
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
для второй конструкции |
|
|
|
|
|
|
|
|
|
|
|
− Мс2 ≤ р2 ≤ Мс2 ; |
− Мс2 ≤ 2 р2 − 5 ≤ Мс2 ; |
|
|
− Мр2 ≤ 2 р2 − 5 ≤ Мр2 ; |
|||||||
− Мс2 ≤ −2 р2 +10 ≤ Мс2 ; |
− Мр2 ≤ −2 р2 +10 ≤ Мр2. |
||||||||||
Таким образом, получили две задачи линейного программирования. Приведем их к стандартной форме, опуская тождественные ограничения.
92

Для первой конструкции
М1 |
+ |
|
р1 |
− у = 5; |
М1 |
− р − у |
|
|
= 0; |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||||||||
с |
2 |
|
|
1 |
|
с |
1 |
2 |
|
|
(4.23) |
|||||
|
|
р1 |
|
|
|
|
|
|
|
|
|
|
||||
М1 |
+ |
− у |
|
= 10; |
М1 |
− р − у |
|
= 0. |
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||||
р |
2 |
|
|
3 |
|
р |
1 |
|
4 |
|
|
|
|
|
||
Первая задача заключается в определении таких М1 |
, М1 |
, р , р |
2 |
, |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
с |
р |
1 |
|
|
уi (i =1, ... 4) , при которых целевая функция (4.21) |
была бы минимальна |
|||||||||||||||
при выполнении ограничений (4.23). Решая ее симплекс-методом, получаем
р = 10 / 3; М1 = 10 / 3; |
М1 |
= 25 / 3; |
|
z = 35 / 3. |
|
||||||||||
1 |
|
|
|
с |
|
|
р |
|
|
|
|
|
|
1 |
|
Аналогично для второй конструкции получаем ограничения |
|
||||||||||||||
− М2 |
+ 2 р |
2 |
+ у |
= 5; |
М2 |
+ 2 р |
2 |
− у |
6 |
= 10; |
(4.24) |
||||
р |
|
|
|
5 |
|
р |
|
|
|
|
|
||||
М2 |
+ 2 р |
2 |
− у |
7 |
= 10; |
− М2 + р |
2 |
+ у = 0. |
|
||||||
с |
|
|
|
|
с |
|
|
8 |
|
||||||
Определяя минимальное значений целевой функции (4.22) при ограничениях (4.24), получаем
р2 = 10 / 3; Мс2 =10 / 3; Мр2 = 10 / 3; z2 = 10.
Если в обеих рамах используются унифицированные элементы, то целевая функция будет иметь вид
z = 50M c + 30M p min
при ограничениях |
|
(4.23) |
и (4.24), |
в |
которых |
следует |
|
принять |
|||||||
Мс1 = Мс2 = Мс |
и |
|
Мр1 = Мр2 = Мр . |
Решая |
|
эту задачу |
линейного |
||||||||
программирования, получаем |
|
|
|
|
|
|
|
|
|
2 |
|
||||
р = 10 / 3; |
р |
2 |
= 5 / 6; |
М |
с |
= 10 / 3; |
М |
р |
= 25 / 3; |
z = 416 |
. |
||||
|
|||||||||||||||
1 |
|
|
|
|
|
|
|
|
3 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Сравним расход z с расходом материала конструкций, изготовляемых по индивидуальным проектам,
z = 35 10 +10 20 = 316 2 . 3 3
Получили, что расход материала в унифицированных конструкциях выше, чем в изготовляемых по индивидуальным проектам, однако унифициро-
93

ванные конструкции могут быть выгоднее с точки зрения технологии изготовления.
Задачи для самостоятельного решения
1. Фирма производит целлофан в виде полотна шириной 150 см, который свертывается в рулоны той же ширины и хранится на складе до тех пор, пока его не разрежут на части меньшей ширины (в соответствии с поступившими заказами). Резальная машина разво-
|
|
|
рачивает полутораметровую |
ленту, и одновре- |
|
|
|
|
|||
|
|
|
менно специально установленные лезвия режут |
||
|
|
|
целлофан на куски меньшей ширины, которые |
||
|
|
|
свертываются в рулоны на другом конце машины |
||
|
|
|
(рис. 4.19). При этом стремятся, кроме рулона за- |
||
|
|
|
казанной ширины, и остальные рулоны получить |
||
|
|
|
таких размеров, на которые может быть спрос. |
||
|
|
|
Например, полутораметровый рулон мож- |
||
|
|
|
но разрезать на три рулона шириной 35 см, одно- |
||
|
|
|
го – 30 см и одного – 15 |
см. Однако если |
|
|
|
|
15-сантиметровый рулон никто не заказывал, он |
||
Рис. 4.19 |
|||||
|
идет в отходы и составляет потерю. |
||||
Учтя все недельные заказы на рулоны разной ширины, можно так организовать работу, чтобы потери были минимальными. Предполагается, что количество широких рулонов достаточно для того, чтобы удовлетворить все недельные заказы.
Сформулировать задачу линейного программирования, если известны данные о заказах текущей недели:
Требуемое количество рулонов, шт. |
|
30 |
|
60 |
|
|
48 |
||
Требуемая ширина рулонов, см |
|
70 |
|
50 |
|
|
40 |
||
|
|
|
2. На неразрезанную жесткопласти- |
||||||
|
|
ческую балку действует импульс, который |
|||||||
|
|
придает в начальный момент времени всей |
|||||||
|
|
балке скорость 2v0. Стоимость балки про- |
|||||||
|
|
порциональна предельным |
пластическим |
||||||
|
|
моментам M10 и M 20 . Найти такие M10 и |
|||||||
|
|
M 20 , при которых стоимость балки с мас- |
|||||||
|
|
сой единицы длины ρ |
минимальна, а оста- |
||||||
|
|
точное перемещение в средине пролета не |
|||||||
|
Рис. 4.20 |
больше заданного значения |
|
(рис. 4.20). |
|||||
u |
|||||||||
94
3. Компания производит полки для ванных комнат типа А и В. Агенты по продажам считают, что в неделю на рынке может быть реализовано
до 550 полок. Для каждой полки типа А требуется 2 м2 материала, а для
полки типа В – 3 м2. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин машинного времени, а типа В – 30 мин. Всего за неделю можно использовать 160 ч машинного времени. Если прибыль от продажи полок типа А составляет 75 руб., а полок типа В – 100 руб., то сколько полок каждого типа следует выпускать в неделю?
4.3.Методы решения многомерных задач
сограничениями на основе преобразования задач
Можно выделить несколько методов преобразования задач, когда исходная нелинейная задача с ограничениями приводится:
–к нелинейной задаче на безусловный экстремум;
–к последовательности решений задач линейного программирова-
ния;
– к последовательности решения нелинейной задачи с линейными ограничениями.
4.3.1. Сведение задачи на условный экстремум к задачам безусловной оптимизации
Все методы в различных вариантах имеют общую черту: преобразование задачи нелинейного программирования с ограничениями либо в одну (эквивалентную исходной) задачу без ограничений, либо в эквивалентную последовательность задач без ограничений. Это можно выполнить тремя методами: методом Лагранжа, методом штрафных функций или методом множителей.
Методы штрафных функций. Наиболее распространенными методами являются так называемые параметрические методы, которые характеризуются наличием одного или нескольких надлежащих образом подобранных параметров, входящих в структуру штрафной функции (которая строится с помощью функций – ограничений) в качестве весовых коэффициентов.
Все параметрические методы подразделяются на три категории:
•методы внутренней точки (метод барьеров);
•методы внешней точки;
•комбинированные методы.
95
В м е т о д а х в н у т р е н н е й т о ч к и значения управляемых параметров постоянно удерживаются внутри допустимой области с помощью штрафной функции. М е т о д ы в н е ш н е й т о ч к и , наоборот, генерируют последовательность точек, которые выходят за пределы допустимой области, но в пределе дают допустимое решение (штрафная функция не позволяет слишком удаляться за пределы допустимой области). В к о м б и н и р о в а н н ы х м е т о д а х в ходе минимизации одни из ограничений удовлетворяются, а другие – нет, однако в пределе все ограничения выполняются при получении оптимального решения.
Итак, пусть задача нелинейного программирования сформулирована следующим образом: найти такой n-мерный вектор параметров оптимиза-
ции х = (х1, х2, … хn)т, |
чтобы |
критерий |
качества был минимален |
( f (x) min ) при выполнении ограничений |
в форме равенств и нера- |
||
венств: |
|
|
|
h j (x) = 0 , |
j = 1, ..., k , |
||
g j (x) ≥ |
0 , |
j = k +1, ..., m , |
|
где f (x), hj (x) и gj (x) – в общем случае нелинейные функции.
Согласно идее штрафных функций сведем эту задачу с ограничениями к задаче на безусловный экстремум функции,
k |
m |
P(xi , ρ i ) = f (xi ) + ∑ ρ ij H j [h(xi )] + |
∑ ρ ijG j [g(xi )]. |
j =1 |
j =k +1 |
Функция P(xi ,ρ i ) называется обобщенной присоединенной (расши- |
|
ренной) функцией или просто штрафной функцией; ρ ij ≥ 0 – весовые ко- |
|
эффициенты; H, G – cпециальным образом выбранные функционалы от соответствующих функций; i – число итерационных этапов оптимизационного процесса.
Требования, налагаемые на функции H и G:
1) |
если ограничения |
в форме равенств, то необходимо, чтобы |
||
H[h(x)] → |
0 при h(x) → |
0 ; |
|
|
2) |
если ограничения в форме неравенств, то необходимо: |
|||
а) чтобы G [g(x)] → |
∞ |
при g(x) → |
0+ , т.е. х определяла точку внутри |
|
области ( g(x) > 0 ); |
|
|
|
|
б) |
чтобы G [g(x)] → |
0 при g(x) → |
0− , т.е. оперируем с внешними |
|
точками;
в) чтобы G [g(x)] > 0 при g(x) < 0 и G [g(x)] = 0 при g(x) ≥ 0 .
96
Таким образом, требования, предъявляемые к функциям, зависят от способа учета ограничений разного вида.
Конкретные методы штрафных функций определяются их видом и правилами перерасчета штрафных параметров по окончании очередного цикла безусловной минимизации.
Приведем наиболее распространенные виды штрафов.
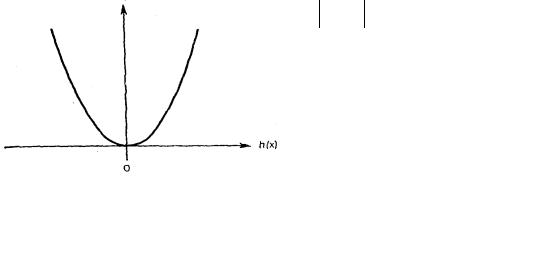
• Квадратичный штраф, который обычно используется для учета Н ограничений-равенств и имеет вид (рис. 4.21)
H = [h(x)]2 .
При минимизации этот штраф препятствует отклонению величины h(x) от нуля. Этот вид штрафа используется как для внешних, так и внутренних точек. В случае ограничений-неравенств их можно привести к ог- раничениям-равенствам, однако для ограничений-неравенств предложены свои виды штрафов.
• Бесконечный барьер: G = 0, если ограничения выполнены, G = ∞ , если ограничения нарушены (рис. 4.22).
Так как в ЭВМ бесконечные величины не используются, то этот вид штрафа записывают в виде
G = 1020 ∑ g j (x) ,
j
где j – число нарушенных ограничений.
+ ∞
|
|
|
n(x) |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.21 |
|
|
Рис. 4.22 |
||
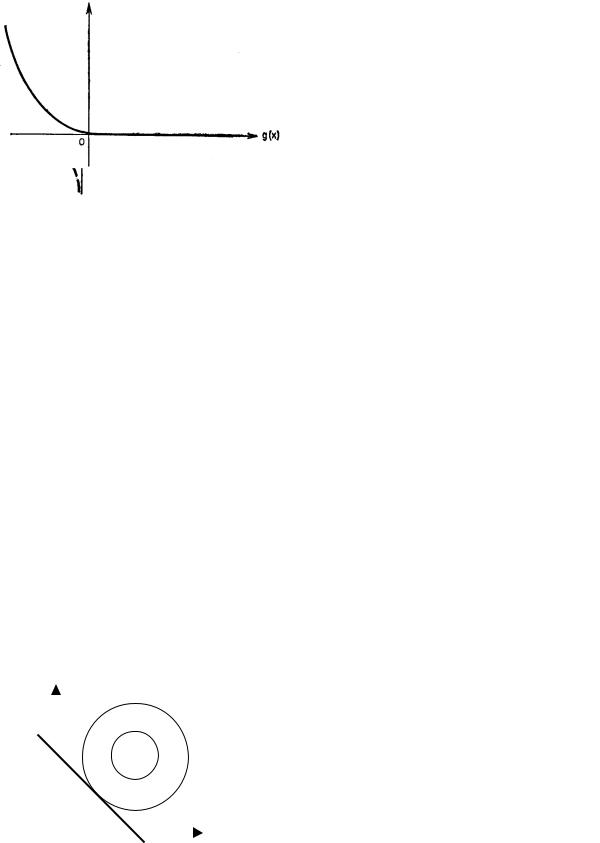
• Логарифмический штраф: |
G = − ln(g(x)) , когда барьерная функ- |
|||||
ция не определена в недопустимых точках (g(x) < 0), а потому методы оптимизации должны предусматривать попадание в допустимую область
(рис. 4.23).
97
Положительный
штраф
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(x) |
|
|
|
|
|
|
|
|
|
|
|
|
g(x) |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отрица- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тельный |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
штраф |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.23 |
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.24 |
|
|
|
|
|
||||||||||
|
• Штраф, заданный обратной |
функцией: G =1/ g(x) – |
барьерный |
|||||||||||||||||||||||||||||||||||||
штраф (рис. 4.24). |
В области |
допустимых значений он всегда положите- |
||||||||||||||||||||||||||||||||||||||
лен. Применяется в методах внутренней точки. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
• Штраф типа квадрата срез- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ки (рис. 4.25). Этот тип штрафа ис- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пользуется в методах внешней |
точ- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ки и имеет вид |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G(x) =< g(x) >2 , |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g(x), если g(x) ≤ |
0; |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.25 |
|
|
|
|
|
|
< g(x) >= |
если |
g(x) > 0. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0, |
|||||||||||||||||
|
Пример 4.13. Минимизировать |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) = (x − 4)2 + (x |
2 |
− 4)2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
при ограничениях разного вида. |
Рассмотрим решение |
при |
одном |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
х2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ограничении-равенстве |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h(x) = x1 + x2 – 5 = 0. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На рис. 4.26 приведено графиче- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ское |
решение |
поставленной |
задачи |
||||||||||||
|
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
х* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( х* = х* = 2,5 ). |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
х1 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решим эту задачу методом штраф- |
||||||||||||||||
|
|
|
|
|
|
|
|
2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
х1 |
+ х2 – 5 = 0 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ных функций. |
Используя квадратичный |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Рис. 4.26 |
штраф, получим |
|
|
|
98 |
P = (x − 4)2 |
+ (x |
2 |
− 4)2 + ρ (x + x |
2 |
− 5)2 min . |
||||||||||||
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
Необходимые условия оптимальности |
|
|
|
|
|
||||||||||||
|
|
∂ P |
|
= 2[x − 4 + ρ (x + x |
2 |
|
− 5)] = 0 ; |
||||||||||
|
|
|
|
||||||||||||||
|
|
∂ x1 |
1 |
|
1 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
∂ P |
= 2[x |
2 |
− 4 + ρ (x + x |
2 |
− 5)] = 0 . |
||||||||||
|
|
|
|||||||||||||||
|
∂ x2 |
|
|
1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Р е ш е н и е : |
|
|
|
|
|
5ρ |
+ 4 |
|
|
|
|
||||||
|
|
|
|
|
x* = x* |
= |
|
. |
|
(4.25) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
1 |
2 |
|
1 + 2ρ |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подсчитаем значения параметров решения в зависимости от ρ.
ρ |
0 |
1 |
10 |
100 |
1000 |
х |
4 |
3 |
2,571 |
2,507 |
2,5007 |
Результаты показывают, что чем больше ρ, тем лучше выполняются ограничения, а решение приближается к точному. Однако при увеличении ρ линии уровней штрафной функции вытягиваются. На рис. 4.27 представлены линии постоянного уровня (а – ρ = 0,5; б – ρ = 2,5; в – ρ = 5а). Такое деформирование ведет к сложности определения безусловного минимума (штрафная функция приобретает овражный характер).
Чтобы преодолеть трудности безусловной оптимизации штрафной функции, решение исходной задачи ведут, используя итерационный процесс: на первом шаге задают не очень большое значение ρ и находят минимум штрафной функции, затем увеличивают ρ, принимая в качестве начальной точки решение, найденное на предыдущем шаге и т.д. Таким образом, трудность нахождения решения во многом зависит от правила, по которому на каждом шаге итерации задают значение параметра ρ, так как если параметр менять довольно медленно, то возрастает число итераций и общее время счета.
Теперь рассмотрим случай, когда ограничение задано в форме неравенства, т.е. найдем минимум функции при ограничении
g(x) = 5 − x1 − x2 ≥ 0 .
Очевидно, что точное решение в этом случае то же, что при ограни- чении-равенстве ( х1* = х2* = 2,5 ). Рассмотрим два вида штрафа.
Штраф типа квадрата срезки
P = (x1 − 4)2 + (x2 − 4)2 + ρ < −x1 − x2 + 5 >2 min .
99
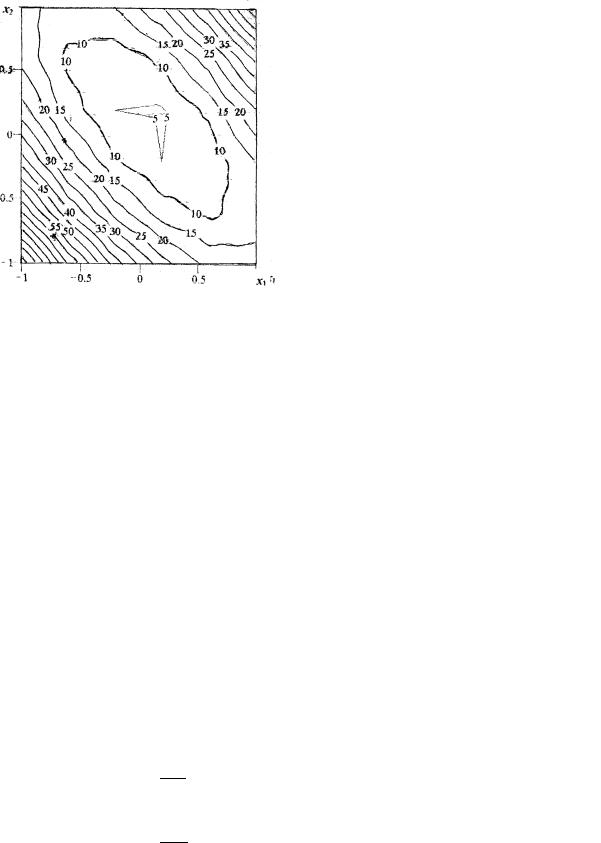
а |
б |
в
Рис. 4.27
Необходимые условия оптимальности:
∂∂ P = 2[x1 − 4 − ρ < −x1 − x2 + 5 >] = 0, x1
∂∂ P = 2[x2 − 4 − ρ < −x1 − x2 + 5 >] = 0 , x2
100
