
Оптимальное проектирование конструкций
..pdfфункцию и не приводит к сильному нарушению ограничений. Это процедура повторяется до тех пор, пока функция может уменьшаться.
Пусть ограничения в рассматриваемой задаче имеют вид
fi (x) = 0, i = 1, …, k ;
(5.49)
fi (x) ≥ 0 , i = k +1, …, m.
Если начальное приближение х0 находится внутри допустимой области, то применим метод наискорейшего спуска, а направление, в котором следует изменять х0 с шагом α > 0, получим из соотношения
|
δ x = −α |
∂ f0т |
(x0 ) = −α f0т(x0 ) . |
|
|
|
|
||
|
|
∂ x |
|
|
Если начальное приближение таково, что fi (x) ≥ |
ε для некоторого i |
|||
и малого параметра ε |
> 0, то определим вектор ограничений |
|||
~ |
для j = 1, …, k и для j > k при |
f j (x0 ) ≤ ε . |
||
f (x) = [ f j (x)] |
||||
Ограничения, для которых f j (x0 ) ≤ ε , называются ε -активными. Та-
кие ограничения должны включаться в рассмотрение, ибо если ими пренебречь, то в процессе выполнения последующих итераций могут возникнуть осцилляции. Для обеспечения малости δ x потребуем, чтобы
δ xтWδ x ≤ ξ 2 , |
(5.50) |
где W – положительно-определенная матрица переменных проектирования (обычно имеющая диагональный вид), а ξ – малая константа.
Таким образом, задача заключается в том, чтобы выбрать δ x , при котором f0 (x0 + δ x) уменьшается, а ограничения не нарушаются. Таким образом, задача состоит в нахождении такой вариации δ x , для которой
δ f0 = |
∂ f |
0 |
(x |
0 |
)δ x ≡ l |
0 |
т |
δ x |
|
|
|
|
|
||||
|
∂ x |
|
|
|
|
|
||
минимально и которая удовлетворяет ограничению (5.49), а также линеаризованным ограничениям
~ |
|
~ |
|
0 |
|
~ |
|
|
|
|
= ∆ f j , j = 1, ..., n |
|
||
|
∂ f |
|
|
|
|
|
|
|||||||
δ f |
= |
|
(x |
|
)δ x ≡ |
l δ x |
|
|
|
|
|
|
, |
|
|
|
≥ |
∆ f |
|
для j > n при f |
|
(x0 ) ≤ ε |
|||||||
|
|
∂ x |
|
|
|
|
j |
j |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
151
где ∆ ~ требуемые уменьшения невязок в ограничениях или границы из f – -
менения функций-ограничений для ε -активных ограничений.
~
Предполагая, что столбцы матрицы l линейно независимы в точках, где несколько ограничений активны ( f j (x0 ) ≤ ε ), можно воспользоваться
условиями теоремы Куна – Таккера и записать необходимые условия оп-
тимальности:
l |
0 |
~~ |
|
|
+ l µ+ 2γ Wδ x = 0, |
|
|
µi (δ fi − ∆ fi ) = 0, i > n, |
(5.51) |
||
γ (δ xтWδ x − ξ 2 ) = 0. |
|
||
Составляющие вектора µ положительны ( i ≥ 0, i > n ), |
как и скалярный |
||
множитель γ (γ ≥ 0) . |
|
|
|
Условия (5.51) нелинейны, что затрудняет нахождение δ x и множителей. Однако можно ожидать, что если ограничения становятся активны-
ми, то они остаются таковыми в течение нескольких итераций. Поэтому
стратегия поиска решения заключается в предположении δ fi = ∆ fi . Тогда
ограничения, имеющие вид произведений, оказываются выполненными, а
для всех переменных будем иметь систему линейных уравнений. При нахождении δ x и µ необходимо следить, чтобы i ≥ 0 при i > n . Если это не
выполняется, то следует исключить соответствующие линеаризованные
ограничения и вновь численно найти решение.
Найдем δ x |
и множители в предположении, что δ fi = ∆ fi . |
Умножив |
||||||||
~т |
|
−1 |
, получим |
|
|
|
|
|
|
|
(5.51) слева на l W |
|
|
|
|
|
|
|
|||
|
|
~т −1 0 |
~т −1~~ |
|
~т |
γδ x = 0. |
|
|||
|
|
l W l |
+ l W l µ+ 2γ l |
|
||||||
|
|
|
|
~ |
~ |
т |
|
|
~ |
|
Из (5.49) и предположения, что δ f |
= l |
|
δ x = ∆ f , будем иметь |
|||||||
|
|
|
|
~ |
~ |
= 0, |
|
(5.52) |
||
где |
|
|
M ff0 + M ff µ+ 2γ ∆ f |
|
||||||
|
|
~ |
|
|
|
|
~ |
~ |
|
|
|
|
|
|
|
|
|
|
|||
|
M ff0 = l тW −1l0 , |
M ff = l |
тW −1l . |
|
||||||
Так как считается, что столбцы матрицы |
~ |
|
||||||||
l линейно независимы и |
||||||||||
W–1 – положительно-определенная матрица, то и матрица M ff |
также по- |
|||||||||
152
ложительно-определенная. Следовательно, систему (5.52) можно разре- |
|||
шить относительно : |
|
|
|
~ |
|
|
|
−1 |
|
|
|
~ |
(M ff0 |
+ 2γ ∆ f ) . |
(5.53) |
µ= −M ff |
|||
Если все компоненты ~ неотрицательны, то это и есть решение, удовлетворяющее условиям Куна–Таккера. Если, с другой стороны, некоторые i оказались отрицательными, то это означает, что такие ограниче-
ния следует исключить из рассмотрения и весь расчет провести заново. Подставив (5.53) в (5.51) и определив проекционную матрицу в виде
|
|
|
|
|
|
~ |
|
~ |
тW −1, |
|
|
|
|
P = I − l M −ff1l |
|
||||||||
получим |
|
|
|
|
|
|
|
|
|
|
|
|
|
δ x = − |
1 |
γδ x1 + δ x2 , |
|
||||||
|
|
|
|
||||||||
где |
|
2γ |
|
||||||||
|
−1 |
|
|
|
|
|
|
|
−1~ |
−1 ~ |
|
1 |
= W |
Pl |
0 |
, |
|
δ x |
2 |
= W |
|||
δ x |
|
|
|
|
l M ff ∆ f . |
||||||
Знание зависимости критерий качества и ограничения от каждой переменной проектирования недостаточно для сложных систем проектирования. Более ценную информацию проектировщик может получить, если
будет знать выгоду, обусловленную ослаблением ограничений, вызванных
сужением их границ.
153
6. МНОГОЦЕЛЕВАЯ ОПТИМИЗАЦИЯ
Одной из проблем, возникающих при разработке методов оптимизации с использованием математического моделирования, является наличие множества показателей качества анализируемых проектов. На начальных этапах исследования предполагалось, что различные, зачастую противоречивые требования к проекту можно тем или иным путем свести к единственному критерию качества. Это возможно, если предположить, что программа нагружения, условия закрепления конструкции и требования, предъявляемые к напряженно-деформированному состоянию, определены единственным способом и единственно само назначение конструкции.
Многокритериальность постановки задачи оптимального проектирования возникает в следующих случаях:
а) если одновременно учитывается работа различных конструкций, для каждой из которых критерии оптимальности различны;
б) учитывается работа одной конструкции, но в разных условиях, например, в переходном режиме и стационарном;
в) работа конструкции оценивается с разных точек зрения, например, материальные затраты, технологичность и др.
Для многокритериальных задач оптимального проектирования можно выделить несколько важнейших особенностей:
1. Множество критериев. Совершенно очевидно, что чем больше критериев вводит конструктор, тем более полное представление о проектируемой машине, о ее возможностях он может получить. Многокритериальная постановка задачи отличается большей близостью к реальной модели и меньшей долей абстракции, и сведение ее к однокритериальной не всегда возможно.
Например, при проектировании автомобиля одним из наиболее важных критериев является расход горючего, который желательно уменьшить. Не менее важным критерием является масса автомобиля. К этим критериям следует добавить стоимость автомобиля, различные прочностные критерии, динамические характеристики (время разгона, устойчивость и т.п.),
х хх степень загрязнения окружающей среды и др. Свести эти критерии к одному практически не-
ххх возможно.
|
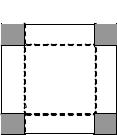
Приведем другой пример. Пусть из желез- |
|
ного листа, имеющего форму квадрата со сторо- |
|
ной l, требуется скроить коробку максимально |
хх |
хх возможного объема при минимальном расходе |
хх материала (рис. 6.1).
Вырезав из листа четыре квадрата с неизвестной пока стороной х и согнув по линиям,
154

отмеченным пунктиром, мы получим коробку, объемом x(l − 2x)2. При этом теряется железо общей площадью 4 x2 . По условию задачи требуется одновременное выполнение двух условий (критериев): x(l − 2x)2 max,
4x2 min. Ясно, что одновременно удовлетворить обоим критериям невозможно: минимальные отходы получаются при х = 0 (не резать вообще),
а максимального объема коробка достигает при x = 1 l . 6
2.Отсутствие критериальных ограничений. Обычно к решению оп-
тимизационной задачи приступают после того, как она математически поставлена. Для задач многокритериальной оптимизации типична обратная ситуация: прежде чем поставить задачу (например, указать множество допустимых решений, среди которых следует искать наилучшее решение), необходимо выбрать критериальные ограничения. Как правило, до проведения специальных расчетов конструктор не может указать обоснованные значения критериев качества. Объясняется это тем, что заранее не известен диапазон изменения критериев качества при изменении параметров управления, а потому постановка таких задач осуществляется в процессе их решения.
3.Трудность выбора единого (решающего) критерия. Отметим, что независимо от того, существует такой критерий теоретически или нет, указать его до проведения расчетов практически невозможно. Это связано прежде всего с очень различным характером критериев, с недостатком сведений о возможностях отдельных критериев, с необходимостью переоценки роли некоторых критериев в зависимости от их реальных возможностей.
Большинство многокритериальных методов основывается на представлении так называемого лица, принимающего решение (ЛПР), т.е. человека, субъективные интересы которого служат основой соизмерения различных частных критериев.
4.Выбор метода. Существуют различные методы решения многокритериальных задач, которые можно разбить на три большие группы:
1)основанные на выявление предпочтений ЛПР и построении единственного критерия качества решения до рассмотрения конкретных альтернатив;
2)диалоговые итерационные человеко-машинные, состоящие в последовательном анализе возможных решений с постепенным выявлением предпочтений ЛПР и переходом к более предпочтительному решению;
3)основанные на предварительном выделении множества неулучшаемых (эффективных) решений и представлении этого множества ЛПР.
155
Постановка корректных задач многокритериальной оптимизации становится возможной только при расширении классического определения экстремума. Естественным обобщением и расширением этого понятия является концепция оптимальности Парето, позволяющая, в частности, расширить круг проблем, рассматриваемых в теории оптимального проектирования, и исследовать принципиальные вопросы проектирования, оптимальные в смысле нескольких критериев качества.
6.1. Множество Парето
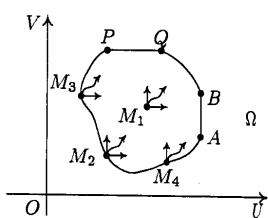
|
Рассмотрим на плоскости (U, V) |
|
множество Q. Каждая его точка облада- |
|
ет одним из следующих свойств: либо |
|
все точки, ближайшие к ней, принадле- |
|
жат множеству Q (такая точка называ- |
|
ется внутренней), либо сколь угодно |
|
близко от нее расположены как точки |
|
множества Q, так и точки, множеству Q |
|
не принадлежащие (такие точки назы- |
|
вают граничными точками множества Q |
|
(рис. 6.2). |
Рис. 6.2 |
Пусть М – произвольная точка |
|
множества Q, внутренняя или гранич- |
ная, (U, V) – ее координаты. Поставим вопрос: можно ли, оставаясь в множестве Q, переместиться из точки М в близкую точку так, чтобы при этом
увеличились обе ее координаты? Если М1 – внутренняя точка, то это бесспорно можно. Если же Мi – граничная точка, то такое возможно не всегда.
Из точек М2, М3, М4 это сделать можно, но из точек вертикального отрезка АВ можно переместиться, только увеличивая координату V (координата U при этом остается неизменной). Аналогично, перемещая точки горизонтального отрезка PQ, мы увеличиваем координату V, координата же U остается неизменной. Что же касается дуги ВQ, то перемещение вдоль нее способно лишь увеличивать одну из координат при одновременном уменьшении другой.
Тем самым точки множества Q можно разбить на три класса:
•точки, которые можно сдвинуть так, чтобы одновременно увеличились обе координаты, при этом точки остались бы в множестве Q (это все внутренние точки множества и часть граничных);
•точки, перемещением которых по множеству Q можно увеличить только одну из координат при сохранении значений второй (точки отрезков АВ и PО);
156
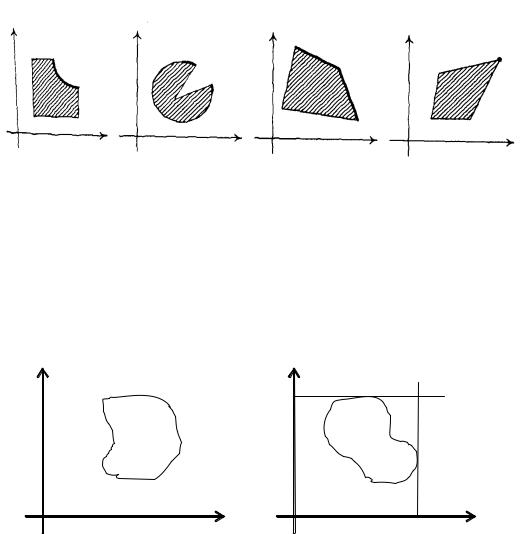
• точки, перемещение которых по множеству Q не способно уменьшить хотя бы одну из координат без одновременного увеличения другой координаты (точки кривой ВО). Множество точек третьего класса называется границей (множеством) Парето данного множества Q.
На рис. 6.3 указаны границы Парето некоторых множеств.
Рис. 6.3
6.2. Постановка задачи
Пусть на плоскости параметров управления (х, у) задано множество ω (рис. 6.4) и в каждой точке этого множества определены непрерывные
функции U = Ф(x, y) и V = Ψ |
(x, y). |
у |
V |
|
Vmax |
ω |
Q |
х |
U |
|
Umax |
Рис. 6.4 |
|
Рассмотрим следующую задачу: на множестве ω |
найти такую точку |
(х0, у0), чтобы |
|
Ф(х0 , у0 ) max и Ψ (х0 , у0 ) max.
Сразу же отметим, что в общем случае поставленная задача решения не имеет.
Действительно, изобразим на плоскости (U, V) все точки, координаты которых вычисляются по формулам
157
U = Ф(x, y), |
V = Ψ (x, y), |
(х, у) ω . |
Обозначим полученное множество через Q. Тогда из рис. 6.4 видно, что наибольшие значения Umax и Vmax достигаются в разных точках, а точка с
координатами (Umax, Vmax) лежит вне множества Q. Тем самым, в исходной постановке задача неразрешима, ибо удовлетворить обоим требованиям одновременно невозможно, поэтому нужно искать компромиссное решение.
Рассмотрим некоторые из известных методов:
•метод идеальной точки;
•метод уступок;
•метод равных и наименьших отклонений.
Два последних метода позволяют многокритериальную задачу свести к однокритериальной.
6.3. Методы решения
6.3.1. Метод идеальной точки
Метод идеальной точки заключается в отыскании на границе Парето точки, ближайшей к точке утопии, задаваемой лицом, принимающем решение. Обычно ЛПР формулирует цель в виде желаемых значений показателей и часто в качестве координат целевой функции выбирает сочетание наилучших значений всех критериев (обычно эта точка не реализуется при заданных ограничениях, поэтому ее называют точкой утопии).
Поясним идею метода на примере.
Пример 6.1. Найти х1 ≥ 0 и х2 ≥ 0 такие, чтобы f1 = x1 + 2x2 max ,
f2 = x1 + x2 min или |
~ |
= −x1 − x2 max |
при условиях x1 + 2x2 ≥ 6, |
f2 |
x1 ≤ 4; x2 ≤ 5. Тогда в плоскости (х1, x2) область допустимых значений –
~
многоугольник с вершинами (0,3), (0,5), (4,1) и (4,5), а в плоскости f1, f2 –
многоугольник с вершинами (6, –3), (10, –5), 6, –5) и (14, –9) (рис. 6.4).
Множество Парето выделено жирными линиями, а точка утопии U(14, –3). Требуется найти на множестве Парето точку А, ближайшую к точке утопии U.
Напишем уравнение прямой, проходящей через две точки с коорди-
натами (10, –5) и (14, 9):
~ |
= af1 |
− 5 =10а+ b |
4 = −4a a = −1. |
||
f2 |
+ b |
=14a + b |
|
b = 5. |
|
|
|
− 9 |
|
||
158

|
|
|
|
x2 |
|
f2 |
|
6 |
10 |
14 |
|
|
|
|
|
|
f1max |
|
|
||||
|
|
|
|
5 |
|
|
|
|
|
f1 |
|
|
|
|
|
-3 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
U(14, –3) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f2min |
|
-5 |
|
|
A |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-9 |
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.4 |
|
|
|
|
|
|
|
Таким образом, уравнение примет вид |
|
|
|
||||||
|
|
|
|
|
|
~ |
|
|
|
|
|
|
|
|
|
|
|
f2 = − f1 + 5, |
|
|
|
||
т.е. |
если |
обозначить |
одну координату |
точки А через |
f * , то другая |
||||||
~* |
|
|
|
|
|
|
|
|
|
1 |
|
= − f |
* |
+ 5 . Расстояние (или квадрат расстояния) s |
2 |
от точки А до точки |
|||||||
f |
2 |
|
|
||||||||
|
1 |
|
|
|
|
|
|
|
|
||
утопии равно (14 − f *) |
2 + (− f * |
+ 5 + 3)2 . |
|
|
|
|
|||||
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
Потребуем, чтобы это расстояние было минимально, тогда получим |
|||||||||
|
|
|
|
(2( f * −14) + 2( f * − 8) = 0 |
|
f * =11; |
|
f * |
= −6. |
||
|
|
|
|
1 |
1 |
|
|
1 |
|
2 |
|
|
|
Таким образом, оптимальные значения критериев в поставленной за- |
|||||||||
даче имеют значения: |
f * = 11; |
f * = − f |
* = 6. Значения параметров найдем |
||||||||
|
|
|
|
|
1 |
2 |
2 |
|
|
|
|
из условий
* +x1* +x1
2x* =11 |
x* = 5; |
x* = 1. |
2 |
||
x2* = 6 |
2 |
1 |
|
|
6.3.2.Метод равных и наименьших отклонений
Вметоде идеальной точки отклонение критериев от своих экстремальных значений было различным. Потребуем, чтобы относительные отклонения всех критериев от своих экстремальных значений были равны и минимальны. При этом предположим, что не существует критерия, оптимизирующего все критерии одновременно.
Условия равенства отклонений запишем в виде
f * − f |
|
|
f * − f |
2 max |
|
|
f |
* |
− f |
m max |
|
|
|
||
1 |
1max |
|
= |
1 |
|
|
= ...... = |
|
m |
|
|
, |
(6.1) |
||
|
f1max |
|
f2 max |
|
|
fm max |
|||||||||
|
|
|
|
|
|
|
|
|
|
||||||
159

где fk* – экстремальное значение k-го критерия при решении многокрите-
риальной задачи, а fkmax – максимальное значение того же критерия при решении однокритериальной задачи.
Предположим, что все критерии должны принимать максимальные значения, тогда соотношение (6.1) можно записать в виде
|
|
|
− f * |
+ f |
|
|
|
− f |
* + f |
k max |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 |
|
|
1max |
|
= |
|
k |
|
|
для любого k =1, ..., |
m |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
fk max |
|
|
|||||||||||||||
или |
|
|
|
|
|
f1max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
− f |
* |
|
|
|
|
− f |
* |
|
+1 |
f * |
|
f * |
g |
|
* |
|
|
|
* |
|
|
||||||
|
1 |
|
+1 = |
|
|
k |
1 |
= |
|
k |
f |
|
− g |
k |
f |
k |
= 0, |
(6.2) |
||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
f1max |
|
|
|
|
fk max |
|
|
|
f1max |
|
fk max |
1 |
1 |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
где |
gk = |
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
fk max |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
В случае, если один из критериев (6.1) максимизируется, а второй, например n, минимизируется, то условие равенства отклонений (6.2) запишется как
g |
f * + g |
n |
f |
* = 2 . |
(6.3) |
1 |
1 |
|
n |
|
Так как относительные отклонения для всех критериев равны, то достаточно сделать эти отклонения минимальными для любого одного критерия k. Пусть k = 1 и все критерии принимают максимальные значения. Тогда, чтобы минимизировать относительное отклонение
f1* − f1max
f1max
нужно f1* увеличить, приблизив его к максимальному значению f1max. Таким образом, решение многокритериальной задачи свелось к решению однокритериальной задачи (нахождению максимального значения f1* с уче-
том дополнительных ограничений (6.3). Если какой-то критерий k должен принимать минимальное значение, то его необходимо учесть ограничени-
ем (6.3).
Пример 6.2. Найти х1 ≥ 0 и х2 ≥ 0 такие, чтобы f1 = x1 + 2x2 max, f2 = x1 + x2 min при условии x1 + 2x2 ≥ 6; x1 ≤ 4; x2 ≤ 5.
160
