
Оптимальное проектирование конструкций
..pdf
f2 (6) = min [(g2 (1,6) + f1(1)), (g2 (2,6) + f1(2)), ....] = = min (252 + 30, 200 + 60, ....) = 260 ;
f2 (7) = min [(g2 (1,7) + f1(1)), (g2 (2,7) + f1(2)), ....] = = min (324 + 30, 265 + 60, ....) = 320 ;
f2 (8) = min [(g2 (1,8) + f1(1)), (g2 (2,8) + f1(2)), ....] = = min (401+ 30, 335 + 60, ....) = 383 ;
f2 (9) = min [(g2 (1,9) + f1(1)), (g2 (2,9) + f1(2)), ....] = = min (480 + 30, 407 + 60, ....) = 450.
На 3-м шаге
f3(l3 ) = min[g3 (l2 , l3) + f2 (l2 )].
l2
Так как l3 задано и равно 10 м, то l2 может принимать значения 2; 3; 4; …; 9, а потому
zmin = f3 (l3 ) = min(476 + 82,418 +114,344 +153,277 + 202,216 + + 260,154 + 320,105 + 383,55 + 405) = 474.
Таким образом, минимальный вес полуфермы из трех панелей при заданной высоте стоек равен 474 кг и достигается при l2 = 7 . Возвращаясь
к предыдущим результатам ( f2 (7) = 320 ), получаем l1 = 3 .
Для того чтобы подобрать размер высоты стоек и конфигурацию сечения стержней, выпишем необходимые соотношения для учета прочности
иустойчивости.
Всилу статической определимости i-й панели будем иметь
N1i = − |
M i −1 |
|
, |
|
|
N2i = Qi − N1i sin α i , |
||
hi −1 cos |
|
|
|
|||||
|
α i |
|
|
|
|
|
||
|
N3i = − |
N2i |
|
, |
N4i = |
M i |
, |
|
|
sin β |
|
|
|||||
|
|
i |
|
hi |
||||
где Мi – изгибающие моменты в точке I простой балки с тем же пролетом,
что и у фермы, Qi – поперечная сила в i-й панели. По условию прочности
Sik ≥ Nσ ik .
Т
121

Применяя известную формулу для критической силы сжатого шарнирно закрепленного стержня длиной а
= π 2 EI
Ркр а2 ,
можно записать условие устойчивости стержня в виде
|
0, |
|
|
|
Nik ≥ 0; |
||
|
|
|
|
2 |
|
если |
|
|
|
|
|||||
Iik = |
|
|
Nik aik |
|
Nik < 0. |
||
|
|
|
|
|
|
|
|
Eπ |
2 |
|
|
||||
|
|
|
|
|
|
|
|
В заключение отметим, что если размерность уравнения Беллмана выше трех, то вступает в силу «проклятие размерности», которое заключается в необходимости производить поиск методом простого перебора при высокой размерности пространства поиска, и метод динамического программирования становится неэффективным.
Пример для самостоятельного решения
На шарнирно опертую по концам балку действует в средине пролета сосредоточенная нагрузка Р = 20 кН. Определить, каким должны быть размеры сечения, чтобы вес балки был минимален, а максимальный прогиб
не превышал заданного значения у0 = 0,001 м, если длина балки 4 м, а
Е = 2·1011 Па.
Рассмотреть два случая: балка круглого сечения и прямоугольного, ширина балки 0,1 м. Полученное решение сопоставить с решением для балки постоянного поперечного сечения.
4.5. Анализ чувствительности
Информация о чувствительности разрабатываемых систем и конструкций к изменениям в проектах, к нарушениям технологии изготовления, внешним воздействиям и другим факторам представляется исключительно важной и позволяет эффективно решать сложные задачи оптимизации.
Основная задача анализа чувствительности заключается в установлении эффективных соотношений между изменениями в проектах конструкции и изменениями ее функциональных характеристик, что позволяет выбрать наиболее эффективные способы оптимизации. Обычно при оптимальном проектировании конструкции имеется широкий выбор переменных проектирования, варьируя которыми можно влиять на величину кри-
122
терия качества. Например, уменьшение веса конструкции может быть достигнуто в результате рационального распределения толщины, управления анизотропией материала, создания предварительного напряженного состояния и др. Важно знать, какие способы оптимизации или их комбинации приводят к большим изменениям критериев качества и каким образом может быть достигнут максимальный выигрыш.
При оптимальном проектировании механических систем и конструкций в роли параметров оптимизации или переменных проектирования обычно выступают геометрические характеристики конструкций, физические характеристики материала и т.п. Каждый из этих параметров определен проектом системы. Однако состояние системы при известных параметрах проектирования обычно описывают с помощью других характеристик, таких как напряжения, перемещения, деформации, которые мы называли параметрами (переменными) состояния. Переменные проектирования и состояния связаны между собой, ибо переменные состояния находят из системы уравнений, определяющих напряженно-деформированное состояние конструкции, в которые входят переменные проектирования. Переменные состояния не зависят от желания проектировщика, если параметры проектирования заданы.
Например, пусть необходимо определить размеры балки, которая должна быть использована в конструкции таким образом, чтобы при приложении заданного множества нагрузок напряжения и отклонения некоторых точек конструкций оказались бы в заданных пределах, а конструкция имела бы, по возможности, малый вес.
Вэтой задаче размеры балки являются переменными проектирования, поскольку они описывают проектируемую конструкцию и должны быть выбраны конструктором. Напряжения и перемещения являются переменными состояния, которые определяются уравнениями равновесия и связью между силой и перемещением. Конструктор не может непосредственно управлять напряжением и перемещением. Он может воздействовать на эти величины только косвенно, меняя размеры балки в конструкции.
Вбольшинстве технических задач проектирования переменные состояния и проектирования легко распознаются. Будем в дальнейшем опи-
сывать n переменных состояния вектором u Rn, а k переменных проекти-
рования – вектором x Rk. Тогда конечно-мерную задачу оптимального проектирования можно сформулировать следующим образом: найти такой вектор x = (x1, x2, …, xk)т, чтобы
f0 (u, x) min |
(4.28) |
при ограничениях |
|
hj (u, x) = 0, j = 1, …, n; |
(4.29) |
123
fi (u, x) ≥ 0, |
i = 1,…., m. |
(4.30) |
На все функции задачи наложено требование существования производных первого порядка. Кроме того, потребуем, чтобы расширенные (n + k)-мерные векторы
|
∂ f |
i |
, |
∂ f |
i |
т |
|
|
|
|
|||
|
|
|
|
|||
|
∂ u |
∂ x |
||||
были линейно-независимы для всех i, для которых fi (u, x) = 0, и чтобы (n× n)-матрица ∂ h/∂ u была неособой. Переменная состояния u должна быть дифференцируема по x, что будет учтено при изложении конструктивных методов.
Если в реальных практических задачах уравнение (4.29) можно решить в замкнутой форме, то сформулированную задачу оптимального проектирования можно записать как задачу нелинейного программирования в терминах переменной проектирования. Однако в некоторых случаях результаты нелинейного программирования могут быть распространены и на случай задач оптимального проектирования в пространстве состояний. В частности, если уравнение (4.29) линейно, то необходимые условия оптимальности в задаче оптимального проектирования записываются так же, как в теореме Куна–Таккера для задач нелинейного программирования.
Рассмотрим другой подход к решению задач оптимального проектирования конструкций, основанный на анализе влияния вариации параметра проектирования на решение задачи (4.28–4.30), который получил название анализа чувствительности проекта.
Критерий качества (4.28) зависит в общем случае как от параметров оптимизации, так и от параметров состояния. Покажем, что зависимость критерия только от параметров проектирования можно получить двумя способами:
•прямым методом дифференцирования;
•методом сопряженных переменных.
4.5.1. Прямой метод дифференцирования
Будем считать, что мы имеем решение задачи (4.28–4.30), которое обозначим через х0, u0. Определим влияние изменения х0 на величину δ х, т.е. посмотрим, как изменится проект, если параметр проектирования
х1 = х0 + δ х. |
(4.31) |
124

Если подставить новую переменную (4.31) в уравнения (4.29), то эти уравнения можно решить относительно новых переменных состояния u1. Поскольку матрица Якоби
J ≡ |
∂ h |
[u0 , x0 ] |
|
||
|
∂ u |
|
неособая, то из теоремы о неявных функциях следует, что если величина
||δ x|| мала, то разность (u1 – u0) тоже мала. Обозначив это изменение через δ u, получим u1 = u0 + δ u.
Используя линейные аппроксимации нелинейных функций, определим, как изменятся характеристики проекта при изменении параметров проекта на величину δ х. Линейные приближения к изменениям величин f0(u, x) и fi (u, x), вызванные малыми изменениями переменных, имеют вид
δ f0[u0 , x0 ] = |
∂ f0 |
[u0 , x0 ]δ u + |
|
∂ f0 |
|
[u0 , x0 ]δ x; |
(4.32) |
|
|
|
|
||||||
|
|
∂ u |
|
∂ x |
|
|||
δ f j [u0 , x0 ] = |
|
∂ f j |
[u0 , x0 ]δ u + |
|
∂ f j |
[u0 , x0 ]δ x . |
(4.33) |
|
|
|
|
||||||
|
|
∂ u |
|
∂ x |
|
|||
В последующих выкладках все функции будут иметь аргументы (u0, |
||||||||
x0), если не оговорено противное. Символ δ |
|
перед обозначением функции |
||||||
означает полный дифференциал этой функции.
Так как параметры состояния u в явном виде неизвестны, то при оп-
|
∂ f |
0 |
δ u |
|
∂ f j |
δ u |
0 |
0 |
|
|
0 |
+ δ u) так- |
ределении |
|
и |
|
учтем, что h( u , x |
|
) = 0 |
и вектор (u |
|
||||
∂ u |
∂ u |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||
же должен удовлетворять уравнению
h( u0 + δ u, x0 + δ x)=0.
Линеаризованный вариант этого условия имеет вид
∂ h |
δ u + |
∂ h |
δ |
x = Jδ u + |
∂ h |
δ x = 0 . |
(4.34) |
|
|
|
|||||
∂ u |
∂ x |
|
∂ x |
|
|||
Это уравнение можно рассматривать как условие, определяющее δ u в виде функции от δ x. Решив его, получим
δu = −J −1 ∂ h δ x .
∂x
125
Подставляя полученное соотношение в уравнения (4.32) и (4.33), можно выразить все члены явно через δ x:
δ f0 = −J |
−1 ∂ h |
∂ f0 |
|
δ x |
+ |
∂ f0 |
|
δ x |
= (−J |
−1 |
∂ h ∂ f0 |
+ |
∂ f0 |
)δ x = l |
0т |
δ х; |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
∂ x |
|
|
∂ u |
|
∂ x |
|
|
∂ x ∂ u |
|
∂ x |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
δ f j = −J |
−1 ∂ h ∂ f j |
|
δ x |
+ |
|
∂ f j |
|
δ x |
|
= (−J |
−1 |
∂ h ∂ f j |
+ |
|
∂ f j |
|
)δ x = l |
j |
т |
δ х. |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
∂ x |
|
∂ u |
|
|
∂ x |
|
|
|
∂ x ∂ u |
|
∂ x |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Компоненты вектора l i |
|
вычисляются по формуле |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
l |
j т |
= −J |
−1 |
|
∂ h ∂ f j |
+ |
|
∂ f j |
|
|
|
|
|
|
|
|
|
|
(4.35) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
∂ x ∂ u |
|
∂ x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
и называются коэффициентами чувствительности функции |
fi |
относитель- |
||||||||||||||||||||||||||||||||||||
но соответствующих переменных проектирования. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Если следовать (4.35), то необходимо вычислить обратную матрицу J–1. Иногда бывает проще численно решить систему (4.29), т.е. вычислить u(x) или использовать другой подход.
4.5.2. Метод сопряженных переменных
Если при вычислении обратной матрицы J–1 размерность n ее очень велика, то процедура обращения оказывается весьма трудоемкой. Чтобы
выразить слагаемые |
∂ f |
0 |
|
δ u |
и |
|
∂ |
f j |
δ u через |
δ x, введем векторы-столбцы λ i |
|||||
∂ u |
|
|
∂ |
u |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
(0 ≤ i ≤ m) как решения сопряженных уравнений |
|
||||||||||||||
|
|
|
т |
λ |
i |
= |
∂ fiт |
0 ≤ |
I ≤ m, |
|
|||||
|
J |
|
|
|
|
|
|
|
, |
(4.36) |
|||||
|
|
|
|
|
∂ u |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где все величины вычислены в точке (х0, u0). Чтобы увидеть пользу этих вновь введенных переменных, вычислим транспонированные значения обеих частей равенства (4.36) и умножим на δ u:
|
i |
т |
∂ f |
i |
δ u . |
|
λ |
|
Jδ u = |
|
(4.37) |
||
|
∂ u |
|||||
|
|
|
|
|
||
Заметим, что член в правой части уравнения (4.37) в точности совпадает с членом, который должен быть исключен из уравнений (4.32), (4.33). Кроме того, произведение Jδ u, которое появилось в уравнении (4.37), может быть выражено при помощи уравнения (4.34):
126

Jδ u = − |
∂ h |
δ x . |
|
||
|
∂ x |
|
Подставив это соотношение в (4.37), получим
∂ f |
i |
δ u = −λ |
i |
т ∂ h |
δ x . |
|
∂ u |
|
|
∂ x |
|||
|
|
|
|
|||
Тогда соотношения (4.32) и (4.33) примут вид
δf0 = −λ 0т
δf j = −λ j т
∂ h |
+ |
∂ f0 |
|
|
|
∂ x |
|
||
∂ x |
|
|
||
∂ h |
+ |
∂ f j |
|
|
∂ x |
∂ x |
|
||
|
|
|||
δ x = l 0тδ x ,
δ x = l j тδ x , |
(4.38) |
где вектор l0 и столбец l i матрицы |
l |
вычислены в точке (х0, u0) согласно |
||||||||
равенству |
|
|
|
|
|
|
|
|
|
|
|
i |
|
∂ f |
т |
|
∂ hт |
|
i |
|
|
l |
|
= |
|
i |
− |
|
λ |
|
, |
(4.39) |
|
∂ x |
∂ x |
|
|||||||
|
|
|
|
|
|
|
|
|||
а компоненты его, как и прежде, называются коэффициентами чувствительности функции fi относительно соответствующих переменных проектирования.
Эти векторы задают в явном виде производные функций критерия качества и ограничений по переменным проектирования, т.е. определяют влияние, которое окажет изменение проекта на критерий качества и огра-
ничения. В частности, если компонента lij положительна, то увеличение xj приведет к увеличению fi. Далее, порядок величины различных коэффициентов чувствительности lij говорит проектировщику о том, какие переменные проектирования значительно влияют на fi , а какие мало влияют.
Различие между двумя формулами для lij (4.39) и (4.34) объясняется
методом рассмотрения члена, связанного с δ u: для уравнения (4.39) нужно вычислить из (4.36) сопряженный вектор λ i для каждого ограничения, которое явно зависит от u. Для уравнения (4.34) нужно вычислить из (4.29)
матрицу ∂ h . Таким образом, в зависимости от числа ограничений и раз-
∂ x
мерности векторов u и x следует отдавать предпочтение одному или другому методу. Однако при наличии большого числа входных условий и ус-
127

ловий нагружения и при больших размерностях векторов u и x вычисления по формуле (4.39) более эффективны.
Пример 4.20. Построим один из векторов чувствительности прочностных ограничений для рассмотренной ранее (пример 4.6) трехстержневой системы. Если система симметричная, то параметрами проектирования
являются площади стержней s = (s1, s2)т, а параметром состояния – пере-
мещение общего узла u = (ux, uy)т. Критерий качества – вес
f0 = ρ g(2s1  2L + s2 L) min .
2L + s2 L) min .
Уравнения равновесия:
|
E 2 |
u |
s |
= P cos α |
, |
|
|
E 2 |
u |
|
(s + 2s |
2 |
) = P sin α . |
(4.40) |
|||||||||
|
|
|
|
y |
|||||||||||||||||||
|
2L |
x 1 |
|
|
|
|
|
|
|
2L |
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Прочностные ограничения: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
f = σ 0 |
− |
E |
(u |
|
+ u |
|
) ≥ 0 , |
|
f |
2 |
= σ 0 |
− |
E |
u |
|
≥ 0 . |
|
|||||
|
|
x |
y |
|
|
y |
|
||||||||||||||||
1 |
|
|
|
2L |
|
|
|
|
|
|
|
|
|
L |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для определения векторов чувствительности используем сначала метод сопряженных уравнений. Якобиан J для уравнения равновесия имеет вид
J = |
E |
2 |
s1 |
0 |
|
2L |
|
s1 + s2 |
, |
||
|
0 |
2 |
|||
а сопряженное уравнение (4.36) для первого прочностного ограничения можно записать в виде
|
|
|
E 2 |
s1 |
|
0 |
|
λ |
1 |
|
|
Е |
1 |
||
|
|
|
|
|
|
+ s2 |
|
* |
1 |
|
= − |
* . |
|||
|
|
|
2L |
|
|||||||||||
|
|
|
0 s1 |
2 |
λ 12 |
|
2L |
1 |
|||||||
Решение этих уравнений: |
|
|
|
|
|
|
|
|
|
||||||
|
|
λ 11 = − 1 |
; |
|
λ 12 |
= − |
|
|
|
|
1 |
|
. |
||
|
|
|
|
2(s1 |
+ s2 |
2) |
|||||||||
|
|
|
|
2s1 |
|
|
|
|
|
|
|
||||
Матрица |
∂ h |
(4.39) задается в виде |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||||
|
∂ s |
|
|
|
|
|
|
|
|
|
|
|
|
||
128
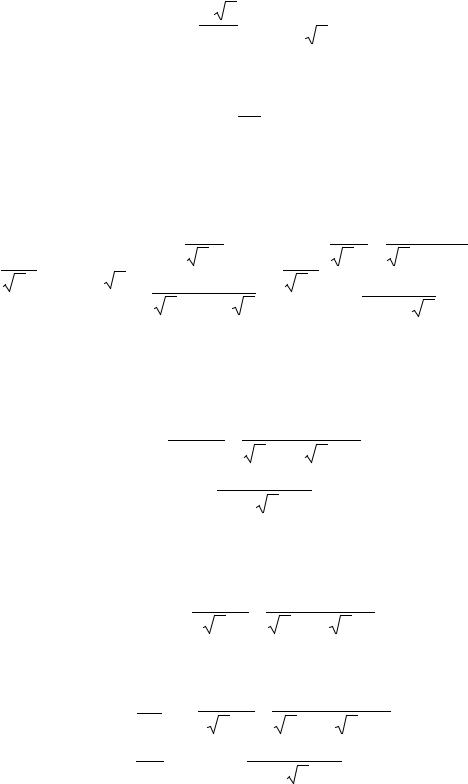
∂ h |
= |
E 2 |
ux |
0 |
|
|
|
|
|
|
|
|
, |
||
∂ s |
2L |
u y |
2 |
||||
|
u y |
|
а производная
∂f1 = 0
∂s 0 .
Подставив эти величины в уравнение (4.39), можно получить вектор чувствительности относительно первого ограничения
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
u |
x |
+ |
|
u y |
|
|
|
l1 = E |
u |
|
u |
|
|
|
|
|
2s1 |
|
|
|
= |
E |
|
|
|
|
|
. (4.41) |
||||
|
|
x |
u y |
y |
|
|
|
|
|
|
|
|
2s1 |
|
2s1 + 2s2 |
|||||||||
2L |
0 |
|
2 |
|
|
|
1 |
|
|
|
|
2L |
|
|
|
u y |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2(s |
+ s |
2 |
2 |
|
|
|
|
|
s |
|
+ s |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
При численных расчетах перемещения определяют из уравнений равновесия (движения) обычно численно. В нашей простейшей задаче они имеют вид (4.40). Подставив их в (4.41), получим
|
P cos α |
+ |
P sin α |
|
|
|
||||
1 |
s |
2 |
2(s |
+ 2s |
2 |
)2 |
|
|||
l |
= |
1 |
|
1 |
|
|
. |
(4.42) |
||
|
|
P sin α |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
(s1 + |
2s2 ) |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Получим тот же вектор, используя второй подход. Для этого подставив решение системы (4.40) в первое прочностное ограничение, получим
f = σ 0 |
− ( P cos α |
+ |
P sin α |
) . |
1 |
2s1 |
|
2(s1 + 2s2 ) |
|
|
|
|
Вектор чувствительности
|
|
|
∂ f1 |
|
P cos α |
+ |
P sin α |
|
|
|
|
|||||
l |
1 |
|
∂ s |
|
|
2s2 |
2(s |
|
+ 2s |
2 |
)2 |
|
, |
|||
|
= |
1 |
|
= |
1 |
|
1 |
|
|
|
|
|
||||
|
|
|
∂ f1 |
|
|
|
|
P sin α |
|
|
|
|
|
|
|
|
|
|
|
∂ s2 |
|
|
|
(s |
+ 2s |
|
|
) |
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
что совпадает с уже найденными значениями (4.42).
129
5.ОПТИМИЗАЦИЯ КОНСТРУКЦИЙ
СРАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
Втеории оптимального проектирования исследуются проблемы определения внутренних свойств и формы конструкции, при которых определенная характеристика ее – критерий качества – принимает экстремальное значение, в то время как некоторые другие механические характеристики находятся в заданных пределах. Континуальный подход основан на непрерывном пространственном описании конструкций. При этом функции состояния (перемещения, деформации, напряжения) и переменные проектирования представляются как функции координат. На переменные проектирования накладываются ограничения из требований технологии и адекватности принятой модели описываемой конструкции. От переменных проектирования могут зависеть коэффициенты уравнений, описывающих поведение конструкции, или форма занимаемой ею области пространства.
К преимуществам континуального подхода следует отнести возможности использования дифференциальных уравнений механики деформируемого твердого тела и получения точных аналитических решений, рассматриваемых в качестве эталонных при применении численных методов,
атакже широкую физическую интерпретацию получаемых результатов. Дискретный подход, ориентированный на вычисление с помощью
ЭВМ, при существующих развитых численных методах позволяет получать решения задач высокой размерности. Этот подход, однако, не всегда оказывается эффективным при исследовании зависимости вида оптимальных проектов от параметров системы.
Исследование вопросов оптимального проектирования систем с распределенными параметрами часто проводят с применением методов вариационного исчисления и оптимального управления.
5.1. Использование вариационных методов для решения задач оптимального проектирования
Вариационные принципы применительно к задачам оптимального проектирования позволяют исключить из рассмотрения дифференциальные связи и устранить необходимость введения сопряженных уравнений. Тем самым понижается порядок общей краевой задачи оптимизации и упрощается вывод условий оптимальности. Кроме того, вариационные принципы и вытекающие из них вариационные неравенства оказываются полезными при аналитических исследованиях оптимизационных задач и обосновании оптимальных решений [3].
Как известно, задачи оптимизации конструкций можно условно разделить по типу оптимизируемых функционалов и виду ограничений на две
130
