
Оптимальное проектирование конструкций
..pdf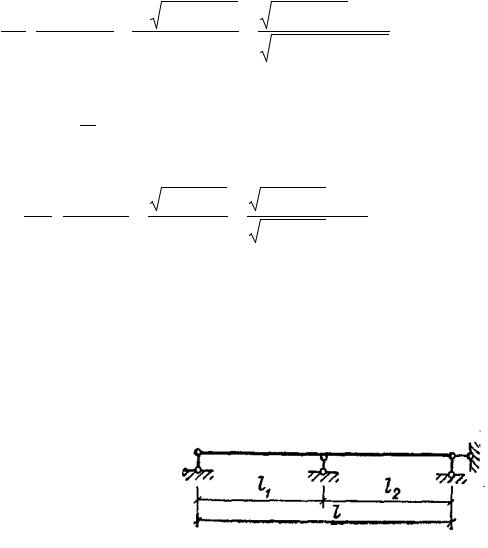
и объем арки
|
|
16 f |
2 |
+ l |
2 |
|
l |
2 |
16 f |
2 |
+ l |
2 |
16 f |
2 |
+ l |
2 |
|
V = |
ql |
|
|
+ |
|
|
|
|
|
+ 4 f |
|||||||
|
16 f |
|
|
|
128 f |
2 |
ln |
16 f |
2 |
+ l |
2 |
. |
|||||
|
[σ ] |
|
|
|
|
|
|
|
|
− 4 f |
|||||||
Если в качестве параметра оптимизации взять отношение стрелы
подъема к пролету w = f , то минимизируемая функция может быть запи- l
сана в виде |
|
|
|
|
|
|
|
|
|
|
|
V = |
ql 2 |
|
16w2 + 1 |
+ |
16w2 |
+ 1 |
ln |
16w2 + 1 |
+ 4w |
. |
|
[σ ] |
16w |
128w2 |
16w2 + 1 − 4w |
||||||||
|
|
|
|
||||||||
Использование необходимого условия оптимальности приводит нас к уравнению, которое не имеет аналитического решения, поэтому для нахождения решения были использованы некоторые из методов, изложенных ранее. В результате получено, что минимальный объем арки достигается
при w = |
|
f |
≈ |
1 |
≈ 0,3418. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
l |
2,93 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 2.3. Оптимизация |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
колеблющейся балки [20]. Опре- |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
делить, при каком соотношении |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
l1 |
|
|
|
|
|
l2 |
|
|||||||
длин l1/l2 низшая частота собст- |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
l |
|
|
|
|
|||||||
венных |
|
колебаний неразрезан- |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
ной балки (рис. 2.9) с равнорас- |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Рис. 2.9 |
|
|
|
|||||||||
пределенной массой m макси- |
|
|
|
|
|
|
|
|
|
|||||||||
мальна. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Р е ш е н и е . Если балка постоянного сечения совершает попереч- |
||||||||||||||||||
ные колебания, то уравнение движения имеет вид |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
EI |
∂ 4 y |
+ ρ F |
∂ 2 y |
= 0, |
|
|
|
|
|
|
|
||
|
|
|
|
|
∂ x4 |
∂ t |
2 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где EI |
– жесткость балки; F – площадь поперечного сечения; ρ – масса |
|||||||||||||||||
единицы объема; t – время.
В случае, если с балкой еще связана равномерно распределенная массовая нагрузка, то в уравнении ρ заменяют на ρ 1 = (1 + е)ρ , где e = q / ρ F ; q – интенсивность внешней равномерно распределенной нагрузки.
41

Если ввести безразмерную координату ξ = x / l (l – длина балки), то уравнение движения примет вид
∂ 4 y |
+ |
ρ Fl 4 |
(1 |
+ e) |
∂ 2 y |
= 0. |
||
∂ ξ 4 |
EI |
∂ t |
2 |
|||||
|
|
|
|
|||||
Решение этого уравнения
y(ξ , t) = ( Asin pt + B cos pt)Y (ξ ),
где р – собственная частота колебаний, а функции формы определяются из уравнений
Y |
IV |
(ξ ) − α |
4 |
где |
α |
4 |
= |
ρ Fp2l |
4 (1 + e) |
|
Y (ξ ) = 0, |
|
|
. |
EI
Таким образом, функции формы можно записать через известные функции Крылова в виде
Y (ξ ) = C1chα ξ + C2shα ξ + C3 cos α ξ + C4 sin α ξ .
Подобное уравнение можно записать для каждого из участков неразрезанной балки:
Yi (ξ ) = C1ichα iξ + C2ishα i ξ + C3i cos α i ξ + C4i sin α i ξ ,
α i 4 = ρ Fp2li 4 (1 + e) ,
EI
где li – безразмерная длина пролета; а ξ – безразмерная координата, отсчитываемая для каждого участка вправо от левой опоры.
Из граничных условий шарнирного опирания
Y1(0) = Y1′′(0) = Y2 (l2 ) = Y2′′(l2 ) = 0
и условий сопряжения в месте расположения опоры
Y1(l1) = Y2 (0) = 0, Y1′(l1) = Y2′(0), Y1′′(l1) = Y2′′(0)
определяем постоянные Cmn и получаем частотное уравнение
cthα 1 + cthα 2 − ctgα 1 − ctgα 2 = 0 .
Решение этого уравнения дано в [20] в табличном виде, а для рассматриваемого случая собственную частоту можно определить по формуле
42
|
p = r |
2 |
EI |
|
|
|
|
r |
|
|
|||
|
Fρ l 4 , |
|
||||
|
|
|
|
|
||
|
|
|
|
|
|
|
в которой r зависит от отноше- |
|
|
|
|||
ния l1/l. Следовательно, реше- |
|
|
|
|||
ние оптимизационной задачи |
|
|
|
|||
свелось |
к нахождению того |
|
|
|
||
значения |
l1/l, |
при котором r |
|
|
|
|
|
|
l1/l |
||||
максимально. |
|
|
|
|
||
|
|
|
|
|
||
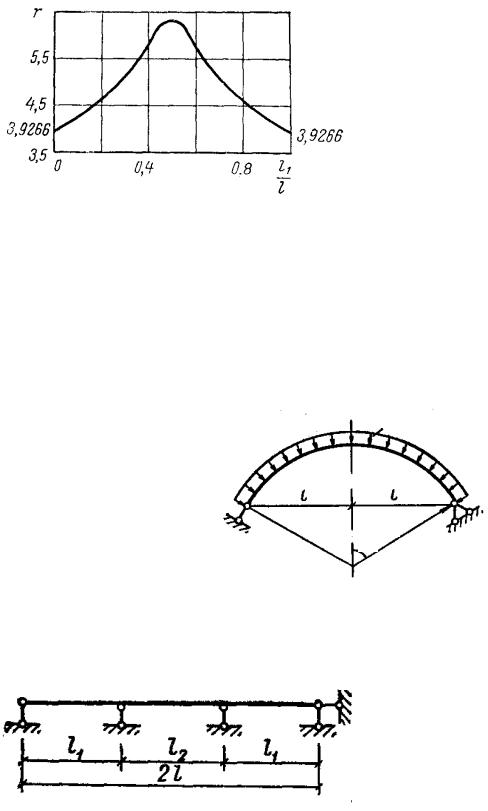
На рис. 2.10 приведена |
|
|
|
|||
|
|
|
||||
графическая зависимость r от |
|
Рис. 2.10 |
||||
l1/l, из которой следует, что
низшая собственная частота поперечных колебаний двухпролетной балки максимальна при l1 = l2 .
Задачи для самостоятельного решения
1. Круговая арка перекрывает пролет 2l и находится под действием равномерно распределенной нагрузки р. Определить значение угла ϕ и ра-
диуса r, минимизирующие объем (вес) арки, удовлетворяющей условиям прочности (рис. 2.11).
2. Определить, при каком соотношении длин l1/l2 низшая частота собственных колебаний неразрезанной балки (рис. 2.12) с равнораспределенной массой m максимальна.
р
l |
|
l |
|
|
|
r
ϕ
Рис. 2.11
l1 |
|
|
l2 |
|
|
|
|
|
|
l1 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2l |
|
|
|
Рис. 2.12
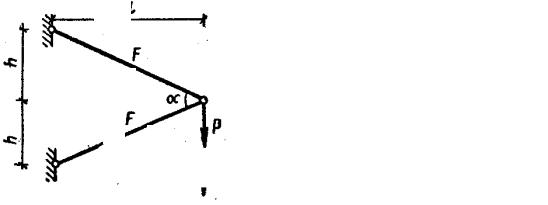
3. Двухстержневые кронштейны (рис. 2.13, а, б) проектируются для восприятия груза Р (расстояния l, h) заданы. Считая, что допускаемое на-
43
l
 F1
F1
F2 α
P
l
F
h
α
F
P
h
a |
б |
Рис. 2.13
пряжение [ σ ] одинаково при растяжении и сжатии, определить значение угла α , минимизирующее суммарный объем двух стержней, удовлетворяющих условиям прочности.
44
3. ЗАДАЧИ МНОГОМЕРНОЙ БЕЗУСЛОВНОЙ ОПТИМИЗАЦИИ
3.1. Постановка и критерии оптимальности многомерных задач безусловной оптимизации
В задачах подобного типа требуется минимизировать f (x) ( х Rn ) при отсутствии ограничений на х, где х – вектор параметров управления размерности n; f – скалярная целевая функция.
Напомним, что точка х* является точкой глобального минимума, если неравенство f (x) − f (x* ) ≥ 0 выполняется для всех х Rn . Когда же это неравенство справедливо лишь в некоторой δ – окрестности точки х* , т.е. для всех х, таких, для которых х− х* < δ при заданном δ > 0, то х* – точка
локального минимума.
Если f (x) – дифференцируемая функция, то градиент функции – век-
тор
|
|
∂ f |
/ ∂ x |
|
|
|
|
|
∂ f |
|
∂ f |
|
∂ f |
т |
f ≡ |
|
|
1 |
|
|
|
т |
|
|
|||||
g(x) = |
∂ f / ∂ x2 |
|
или |
g |
|
(x) = |
|
, |
|
,..., |
|
. |
||
|
∂ x1 |
∂ x2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂ xn |
|||
|
|
∂ f |
/ ∂ xn |
|
|
|
|
|
|
|
|
|
|
|
Если вычислить вторую производную от минимизируемой функции, то получим симметричную квадратную матрицу Гессе
|
|
|
|
|
|
∂ 2 f |
|
|
|
∂ 2 f |
|
|
|
∂ 2 f |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ x12 |
|
|
∂ x1∂ x2 |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
∂ x1∂ xn |
||||||||||
|
2 |
|
|
|
|
∂ 2 f |
|
|
|
∂ 2 f |
|
|
|
∂ 2 f |
|
|
||||
|
f |
≡ |
G(x) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||
|
∂ x1∂ x2 |
|
|
|
∂ x22 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
∂ x2∂ xn |
||||||||||
|
|
|
|
|
|
∂ 2 f |
|
|
|
∂ 2 f |
|
|
|
∂ 2 f |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂ x1∂ xn |
|
∂ x2∂ xn |
|
|
|
∂ x2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
||
Необходимое условие стационарности g(x*) = 0.
Если исходную функцию f (x) можно разложить в ряд Тейлора:
f (x* + ∆ x) = f (x* ) + g т(x* )∆ x + 1 (∆ x)тG(x* )∆ x + ... , 2
где ∆х – вектор изменения х, то знак приращения функции в точке стационарности ∆ f = f (x* + ∆ x) − f (x* ) определяется квадратичной формой
45

∆ f = 1 (∆ x)тG(x* )∆ x . 2
Из линейной алгебры известно, что знак этого приращения зависит от свойств матрицы G, а именно:
∆ f > 0, |
если G – определенно-положительна; |
|
∆ f ≥ |
0, |
если G – полуопределенно-положительна; |
∆ f < 0, |
если G – определенно-отрицательна; |
|
∆ f ≤ |
0, |
если G – полуопределенно-отрицательна. |
Можно привести формулировку необходимых и достаточных условий существования минимума функции нескольких переменных:
• для наличия в точке х* локального минимума необходимо, чтобы выполнялось равенство f (x* ) = 0 и матрица вторых производных
2 f (x* ) была положительно полуопределенной;
•достаточным условием наличия в точке х* локального (изолированного) минимума является f (x* ) = 0 , 2 f (x* ) – положительно определена.
Если удается доказать, что (∆ x)т 2 f (x* )∆ x ≥ 0 для всех х, то f(x) на-
зывается выпуклой функцией, а локальный минимум оказывается глобальным.
Пример |
3.1. |
[16]. Рассмотрим |
функцию f (x) = 2x |
2 |
+ 4x x3 |
– |
||||||
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
|
−10x x |
2 |
+ x |
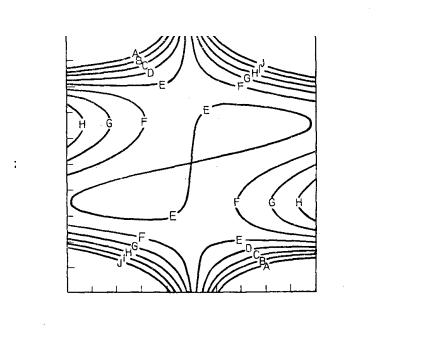
2 , линии уровня которой показаны на рис. 3.1. Необходимо |
|||||||||
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
классифицировать точку x* = [0,0] т . |
|
|
|
|
|
|
||||||
Р е ш е н и е . Градиент функции |
|
|
|
|
|
|
||||||
|
|
|
f (x |
* |
|
4x1* + 4(x2* )2 −10x2* |
|
0 |
|
|
|
|
|
|
|
) = |
|
|
= . |
|
|
|
|
||
|
|
|
|
|
12x1* (x2* )2 −10x1* + 2x2* |
0 |
|
|
|
|
||
Следовательно, точка х* – стационарная точка.
Классифицируем точку х* , для чего подсчитаем значения вторых производных:
∂ 2 f |
= 4, |
∂ 2 f |
= 24x x |
2 |
+ 2, |
|
|
|
|
||||
∂ x 2 |
|
∂ x |
2 |
1 |
|
|
|
|
|
|
|||
1 |
|
|
2 |
|
|
|
46
|
|
∂ 2 f |
=12x2 |
−10, |
|
|
|
||
|
|
∂ x1∂ x2 |
2 |
|
|
|
|
|
|
а потому |
4 |
−10 |
|
|
2 f (x* ) = G(x* ) = |
. |
|
||
|
−10 |
2 |
|
|
f (x) = 2х12 + 4х1х23 −10х1х2 + х22
2,40
1,20
x2
0,00
–1,20
–2,40
–2,40 –1,20 0,00 1,20 2,40
x1
Рис. 3.1
Линии
уровня А – 40,000 В – 30,000 С – 20,000 D – 10,000 Е – 0,000 F – 10,000 G – 20,000 H – 30,000 I – 40,000 J – 50,000
Эта матрица является неопределенной, так как элементы главной диагонали положительны, а определитель матрицы отрицателен. Следова-
тельно, х* – седловая точка, что и отражено на рис. 3.1.
3.2. Методы решения многомерных безусловных задач
Использование необходимых условий оптимальности для решения многих задач проектирования затруднительно, так как в большинстве случаев мы получаем нелинейную систему уравнений. Поэтому разработано большое число численных методов решения.
Работа любого метода оптимизации состоит из двух этапов:
1)вычисление в начальной точке предусмотренных методом характеристик (значений функции, иногда значений производных);
2)по полученной на первом этапе информации строится приближение к решению. Обычно это сводится к переходу в новую точку, в которой
47
значение функции уменьшается. Каждый из алгоритмов отличается способом выбора этой новой точки.
Все численные методы итерационные. Для многих из них очередная точка xk +1 выбирается по значению предыдущей согласно алгоритму
xk +1 = xk + α k pk , |
(3.1) |
|
где α k – шаг изменения (число); |
pk – вектор направления, вдоль которого |
|
происходит переход от точки xk |
к точке xk +1 . |
|
Если для определения точки xk +1 используется информация не только с предыдущего k-го шага, но и с других (k – 1, k – 2, …), то такие алгоритмы называются самообучающимися.
Чаще же для организации итерационного процесса используется соотношение (3.1), и обычно название метода минимизации определяется
способом выбора направления pk , а вариант метода зависит от способа выбора длины шага α k . Трудности решения задачи определяются числом
переменных и видом целевой функции.
Методы решения задач безусловной оптимизации отличаются относительно высоким уровнем развития по сравнению с другими методами нелинейного программирования. Все методы можно условно разделить на три класса в соответствии с типом используемой при реализации того или иного метода информации:
1)методы прямого поиска, основанные на вычислении только значений целевой функции;
2)градиентные методы, в которых используются точные значения первых производных f (x);
3)методы второго порядка, в которых наряду с первыми производными используются также вторые производные функции f (x).
Отметим, что ни один метод или класс методов не отличается высокой эффективностью при решении задач различных типов. Например, в некоторых задачах вычисление целевой функции требует чрезмерных затрат времени, в других задачах получить решение с очень высокой степенью точности невозможно, иногда весьма затруднительно найти аналитическое выражение производных целевой функции. Поэтому инженер должен осознанно выбирать тот или иной метод, исходя из его достоинств и недостатков.
48
3.2.1.Методы оптимизации, не связанные
свычислением производных
Эти методы еще называются методами прямого поиска и используются для оптимизации непрерывных и разрывных функций, однако функции должны быть унимодальны. Суть методов состоит в сопоставлении значений функций в определенных точках. Это относится и к методам сокращения интервалов, которые использовались для решения одномерных задач, однако в случае многомерных задач эти методы неэффективны, так как сравнение надо вести на решетке n-размерности, в результате чего и объем вычислений сильно возрастает, даже существует специальный термин – «проклятие размерности».
Все методы данного класса условно можно разделить на эвристические и теоретические. В эвристических методах поиск оптимальной точки ведут на основе интуитивных геометрических представлений, а в теоретических – на основе фундаментальных математических теорем. Рассмотрим один из самых распространенных эвристических методов – метод поиска по симплексу или метод многогранника, как вариант этого метода – метод сопряженных направлений.
Метод поиска по симплексу. Существуют разные варианты этого метода. Вначале рассмотрим вариант, предложенный Нелдером и Мидом. В n-мерном пространстве по определенному правилу выбирается (n+1) точка. Эти точки можно интерпретировать как вершины многогранника (отсюда название метода). Если точки выбраны таким образом, что они являются равноотстоящими друг от друга вершинами, то такой многогранник называют регулярным симплексом (отсюда другое название метода). После определения значений функции в каждой из вершин их нумеруют таким образом, чтобы выполнялось неравенство
f (xn +1) = fn +1 ≥ fn ≥ fn −1 ≥ .... ≥ f1,
т.е. в вершине (n+1) функция принимает максимальное значение («худшая» из вершин, если решается задача нахождения минимума функции; в дальнейшем координату «худшей» вершины будем обозначать как xh , а
значение функции в ней fh ), а в первой вершине – минимальное значение
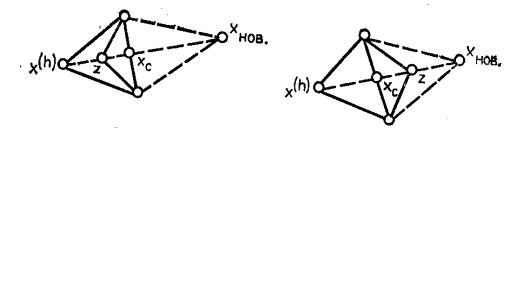
(«наилучшая» вершина). Согласно алгоритму на каждом шаге итерации избавляемся от «худшей» вершины (рис. 3.2).
Если обозначить через хс центр тяжести лучших n вершин
|
1 |
n |
|
xc = |
∑ x j , |
||
|
n j =1
49
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хнов |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
х |
(h) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хс |
|
|
|
|
|
хнов |
|
|
|
|
|||||
|
|
|
|
|
|
|
а |
|
|
|
|
|
|
|
|
х |
(h) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хнов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хнов |
|
|
|
|
|
|
х |
(h) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
хс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
х(h) |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
хс |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
в |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 3.2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
то можно построить новую точку xнов = xc + α (xc − xh ), |
|
( α > 0 – коэффи- |
|||||||||||||||||||||||||||||||||||
циент отражения) и вычислить f (xнов) . В этом случае говорят, что точка xнов получена отражением точки хh . При этом могут возникнуть три слу-
чая:
1) f1 ≤ fнов ≤ f N , т.е. точка xнов – не лучшая, но и не худшая из всех вершин, поэтому заменяем в многограннике вершину хh на xнов (строим
новый многогранник, рис. 3.2, а) и переходим к следующей итерации;
2) fнов < f1 , т.е. xнов оказалась лучшей, а потому многогранник рас-
тягиваем в этом направлении, определяем новую точку x p = xc + γ (xнов − хс) , где γ > 1 представляет собой коэффициент растяже-
ния (рис. 3.2, б). Если f p < fнов, то xнов заменяем на хри переходим к следующей итерации. В противном случае заменяем в многограннике вершину хh на xнов ;
3) fнов > f N , т.е. xнов оказалась худшей среди всех вершин (шаг неудачный, рис. 3.2, в, г), а потому многогранник сжимаем, определяя новую точку
x |
x |
c |
+ β (x |
h |
− x |
c |
) |
при |
f |
нов |
≥ f |
h |
, |
= |
|
|
|
|
|
|
|
||||||
сж |
xc + β (xнов − хс |
при |
fнов < fh . |
||||||||||
50
