Оптимальное проектирование конструкций

Умножив левую и правую часть на а, получим

так как as′′ = 0 из условия допустимости направления.

Из (4.29) можно найти коэффициент γ = (aaт)−1as, и подставив его в

(4.28), получим

s = aт(аат)−1аs + s′′ ,

откуда

s′′ = [I − aт(аат)]s,

где I – единичная матрица.

Обозначим через Р = I − aт(аат) – проективную матрицу, тогда, вы-

брав произвольным образом направление s, всегда можно получить допустимое направление согласно s′′ = Ps . Если s = − f (x) , то получим метод

раничениях h(x) = 2x1 + x2 − 3; x1 ≥ 0; x2 ≥ 0.

Р е ш е н и е . Выберем в качестве начальной допустимую точку x0 = [1,5; 0]т. Построим проективную матрицу

111

Подсчитаем градиент функции:

Определив α из условия минимума функции в точке х1 ( α = − 0,83 ), найдем решение задачи: x1 = [1, 1]т.

4.4. Динамическое программирование

Динамическое программирование представляет собой математический метод для нахождения оптимальных решений многошаго-

вых (многоэтапных) задач. Некоторые из таких задач естественным образом распадаются на шаги (этапы), но имеются задачи, в которых разбиение производится искусственно.

Метод применяется для управляемых процессов. Процесс является управляемым, если можно влиять на ход его развития. Под управлением же понимается совокупность решений, принимаемых на каждом этапе для влияния на ход развития процесса. Метод позволяет одну задачу со многими переменными заменить рядом последовательно решаемых задач с меньшим числом переменных. Это значительно сокращает объем вычислений и ускоряет процесс принятия решений.

Основным принципом, на котором базируется оптимизация многошагового процесса и особенности вычислительного метода динамического программирования, является принцип оптимальности Беллмана, который формулируется следующим образом: каково бы ни было состояние систе-

мы перед очередным шагом, выбирать управление на этом шаге надо так,

112

чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах были оптимальными. Другими словами, решение на ка-

ждом последующем шаге должно приниматься с учетом результата, полученного на предыдущих шагах. Далее будет показано, что этот математический принцип имеет довольно простую математическую интерпретацию, выражающуюся в составлении определенных рекуррентных соотношений.

Согласно другому принципу, природа задачи, допускающая использование метода ДП (динамического программирования), не меняется при изменении количества шагов, т.е. форма такой задачи инвариантна относительно числа шагов N. В этом смысле каждый конкретный процесс с заданным N оказывается как бы вложенным в семейство подобных ему процессов (принцип вложения).

Реализация названных принципов дает гарантию того, что, вопервых, решение, принимаемое на очередном шаге, окажется наилучшим с точки зрения всего процесса в целом (а не узких интересов данного этапа) и, во-вторых, последовательность решений одношаговой, двухшаговой и т.д. задач приведет к решению исходной N-шаговой задачи.

Полезно обратить внимание на специфические особенности построения схем ДП. Обычно они строятся так, что первым исследуется конечный этап того реального явления, которое отражено в задаче оптимизации. Действительно, этот этап может быть изучен и спланирован сам по себе наилучшим (в смысле критерия оптимизации) образом, поскольку он завершает процесс. Но сделать это можно лишь на основе предположений об ожидаемых исходах предшествующего (но еще не исследованного) этапа.

Завершив последний этап, нужно рассмотреть аналогичную задачу применительно к предпоследнему этапу оптимизации, но потребовать при этом, чтобы экстремальное значение критерия, которое можно получить на этом этапе, было достигнуто с учетом двух последних этапов вместе.

Рассмотрим задачу о минимальном расходе горючего самолетом при наборе высоты и скорости, поясняющую идею ДП.

Пример 4.18. Миниминизация расхода горючего самолетом. Самолет, находящийся на высоте Н0 и имеющий скорость V0, должен подняться на высоту Hk и приобрести скорость Vk. Известен расход горючего при подъеме самолета с любой высоты Hi на любую (Hi + ∆Hi) при постоянной скорости, а также расход горючего при увеличении скорости от любой Vi

до любой (Vi + ∆Vi) при неизменной высоте. Найти оптимальное управление набором высоты и скорости, при котором общий расход горючего минимален.

113

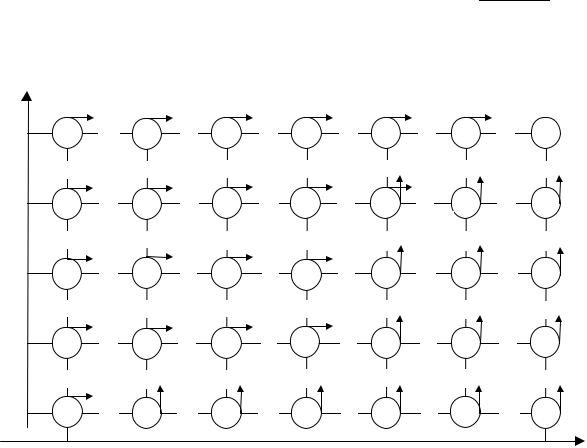
Р е ш е н и е . Из условия задачи следует, что состояние системы в любой момент времени t определяется функцией S = S(V, H), поэтому решение будем искать в плоскости V, H, а точнее в области, ограниченной

прямыми V0 и Vk, а также H0 и Hk, которая является областью допустимых

состояний. Начальное состояние S0(V0, H0) и конечное Sk(Vk, Hk) определены как две точки плоскости V, H.

Чтобы построить решение методом ДП, разобьем отрезок (Hk–H0) на n1, а (Vk–V0) на n2 равных частей (этапов) и условимся считать, что за один

шаг (этап) самолет может увеличить либо высоту на ∆ H = H k − H 0 , либо

Из них нужно выбрать ту траекторию, при которой общий расход горючего, равный сумме расхода на каждом этапе, будет минимален. Если n1 и n2 велики, то общий перебор требует очень много времени. Использование же ДП позволяет решить эту задачу проще и быстрее.

Изобразим на чертеже на вертикальных линиях расход горючего при наборе высоты с постоянной скоростью, а на горизонтальных – расход го-

114

рючего при увеличении скорости при постоянной высоте. Пусть n1 = 4, n2 = 6, всего n1 + n2 = 10 этапов.

Оптимизацию начинаем с последнего этапа, т.е. с точки Sk. В нее

можно прийти либо из А1, либо из А2, причем для каждого такого шага управление единственно. Обозначим минимальный расход горючего при таких шагах цифрами в кружках в А1 и А2, а условия оптимальности управления, приводящие к этому расходу, будем обозначать стрелкой.

Итак, последний десятый шаг спланирован, поскольку найдены условия оптимального управления (либо набор высоты, либо увеличение скорости) и определен расход, соответствующий этим управлениям.

Переходим к девятому этапу. В А1 и в А2 можно попасть из точек В1, В2 и В3. Найдем условно оптимальные управления для каждого из трех возможных состояний. Из В1 можно попасть в Sk только через А1 с суммарным расходом 9+8 = 17 единиц; из В2 – через А1 (суммарный расход – 18) и через А2 (суммарный расход – 24), но минимальное (оптимальное) управление будет через А1, его и записываем в В2 с указанием стрелки; из В3 –

только через А2. Условно оптимальное управление выбрано, следовательно, этот этап завершен.

Переходим к восьмому этапу, на котором возможны четыре состояния (С1, С2, С3, С4). Для С1 и С4 – управления единственны и расходы равны 27 и 34. Из С2 можно попасть в В1 и В2, при этом расход одинаков и равен 25. Стрелкой указываем оба направления. Для С3 оптимальным являет-

ся переход через В2, при этом расход равен 28.

На последнем этапе выбираем оптимальное управление и суммарный расход, равный 88, и таким образом находим оптимальное управление в целом.

Упрощенный процесс решения задачи обусловлен тем, что не учитывалась возможность одновременного набора высоты и скорости. Чтобы это учесть, достаточно на рис. 1 провести диагональные линии, т.е. разре-

шить, например, переход из точки В2 в Sk с указанием расхода. Остальные рассуждения будут аналогичны.

В оптимальном проектировании конструкций нашли применение несколько модификаций динамического программирования. Рассмотрим один из них.

Пусть требуется найти вектор х, доставляющий минимум функции

Задачу можно интерпретировать как задачу оптимального распределения некоторого количества а между n объектами. Введем функцию

115

которая называется функцией Беллмана и определяет оптимальное распределение количества α ≤ а между i ≤ n объектами, так что

n

∑ x j = α .

j =1

Тогда задачу распределения количества а между n объектами можно представить такой последовательностью шагов:

1-й шаг: j = 1, f1(α ) = g1(α ). На этом шаге минимизации пока нет:

все количество а поступает на единственный первый объект, а а принимает дискретные значения в диапазоне 0 ≤ α ≤ а;

Это уравнение носит название уравнения Беллмана. Когда процесс доходит до i = n , исходная задача оказывается решенной. Значение xn находится непосредственно из последнего шага, а предыдущие значения неизвестных находятся последовательно: сначала xn–1, затем xn–2 и т.д. (обратный ход процесса ДП). Приведем пример решения задачи.

116

Сведем данную задачу к задаче математического программирования, для чего разобьем стержень на три подобласти. В каждой подобласти толщина стержня постоянна. Обозначим площадь сечения стержня на i-м

участке через Si (i = 1, 2, 3). Тогда оптимизационную задачу можно сформулировать следующим образом: найти такой трехмерный вектор S = (S1, S2, S3), чтобы критерий качества

Р е ш е н и е . Запишем уравнение изгиба балки для каждой из подобластей и состыкуем решения в каждом i-м сечении. Тогда прогиб на свободном конце можно записать в виде

y(L) = Pl3 ( 1 + 19 + 7 ), 81E I3 I1 I2

где Ii – момент инерции i-го сечения, который может быть выражен через площадь сечения,

Ii = α k Sik .

Как было показано ранее, α и k зависят от формы сечения (например,

если сечение круглое, то k = 2, α k = 1 , а если сечение в форме прямо- 2π

угольника и в качества параметра управления выступает высота сечения,

то k = 3, α k = 1 ). Будем решать задачу методом динамического про12b2

граммирования, начиная со свободного конца. Для 3-го участка балки функция Беллмана

f1 = ρ gS3 min,

при этом должно выполняться ограничение

На этом этапе оптимизационной задачи нет, так как минимальное значение функции будет при минимальном значении S3, которое может быть найдено из ограничения

117

т.е. из этого уравнения можно выразить S3 min = ϕ (S1, S2 ) при известном

профиле сечения.

На втором шаге согласно уравнению Беллмана находим минимум функции f2:

без каких-либо ограничений, а потому минимальное значение можно найти из обычного условия

∂f2 = 0 ,

∂S2

которое позволяет выразить S2 через S1, тогда S2 min = ϕ (S1) . Переходим к последнему шагу. Согласно уравнению Беллмана

назад, определяем и все остальные переменные проектирования.

В заключение приведем другие возможные формулировки задач, которые можно решить методом динамического программирования.

1. Задача минимизации функции

n

z = ∑ g j (x j −1, x j ) min

j =1

без ограничений. В этом случае функция Беллмана имеет вид

а уравнение Беллмана

Процесс решения по-прежнему заключается в последовательности решения минимизации задач (уравнения Беллмана) при дискретном изменении x j и запоминании результатов решения.

118

2. Задачей более общего вида является задача минимизации по двум переменным.

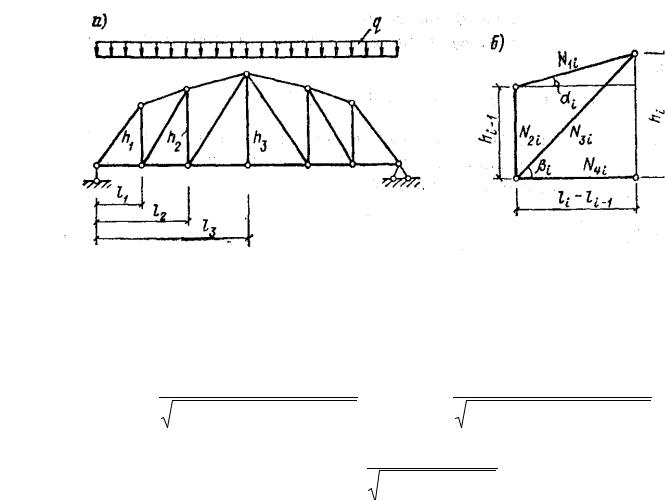
Пример 4.20. Оптимальное проектирование симметричной фермы [13]. Симметричная балочная ферма с восходящими раскосами перекрывает пролет 20 м и несет равномерно распределенную нагрузку q. Ферма

имеет три панели. Считая на первом этапе заданными высоты стоек h1, h2 и h3 , найти длины панелей, отвечающие минимуму веса (рис. 4.33).

Рис. 4.33

Р е ш е н и е . Рассмотрим i-ю панель фермы (рис. 4.33, б), где

Вес каждой панели зависит только от положения ее границ:

панели при фиксированных значениях ее границ) и запишем их в таблицу.

119

Для первой панели уравнение Беллмана имеет вид

f1(l1) = min g1(l0 , l1) = g1(0, l1),

l0

так как l0 = 0. Таким образом, возможные значения f1(l1) расположены в

верхней строке таблицы (если длина первой панели 1 м, то ее вес равен 30 кг, если длина 2 м, то 60 кг и т.д.).

На втором шаге уравнение Беллмана примет вид

f2 (l2 ) = min[g2 (l1, l2 ) + f1(l1)].

l1

Если l2 = 2 , то возможно только значение l1 = 1, так как 0 < l1 < l2 , а потому

f2 (2) = min[g2 (1,2) + f1(1)] = 52 + 30 = 82.

Если l2 = 3 , то возможны значения l1 = 1 и l1 = 2 , а потому

f2 (3) = min[(g2 (1,3) + f1(1)), (g2 (2,3) + f1(2))] = min(84 + 30,56 + 60) = 114.

Аналогично получаем

f2 (4) = min[(g2 (1,4) + f1(1)), (g2 (2,4) + f1(2)), (g2 (3,4), f1(3))] = = min(129 + 30,93 + 60,58 + 110) = 153;

f2 (5) = min [(g2 (1,5) + f1(1)), (g2 (2,5) + f1(2)), ....] = = min (186 + 30, 142 + 60, 100 + 180) = 202;

120