Теоретическая механика избранные задачи студенческих олимпиад ПНИПУ

Содержание

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

3

Предисловие к первому изданию

Студенческие олимпиады ПГТУ (ППИ) по теоретической механике проводятся с 1974 г. В них приняли участие около 4600 студентов. Форма проведения олимпиад неоднократно изменялась, так как учитывался накопленный опыт и изменялись учебные планы.

В1974 г. все задачи были по динамике. В 1975 г. олимпиада проводилась в два тура. Первый (заочный) тур был отборочным, второй – основным. В каждом туре были задачи по статике и по динамике, причем соревнования по статике и динамике проходили отдельно (в них участвовали студенты разных курсов); фактически проводились параллельно две олимпиады. В 1976 г. олимпиада проводилась в один тур, и были задачи по всем трем разделам механики (статика, кинематика, динамика), соревнования по которым проходили отдельно; фактически проводились параллельно три олимпиады. В 1977–1999 гг. эта система проведения олимпиады в основном сохранялась. Изменения касались только соревнования по кинематике: иногда оно не проводилось, а иногда было объединено

ссоревнованием по статике. В 1974–1999 гг. олимпиада проходила (один раз в год) в апреле или в мае, за исключением 1990 г. (декабрь) и 1991 г. (не проходила по техническим причинам). Начиная

с2000 г., ежегодно проводятся две олимпиады – одна в апреле или в мае, другая – в декабре. В 2000 г. весенняя олимпиада проходила по всем трем разделам механики (отдельные соревнования), а зимняя – только по динамике. В 2001–2002 гг. весенняя олимпиада была посвящена только кинематике, а зимняя – только динамике. В 2003–2006 гг. обе олимпиады были по динамике. Весенняя олимпиада 2007 г. также была только по динамике. Начиная с зимы 2007 г. и по настоящее время (2009 г.) каждая из двух ежегодных олимпиад содержит задачи по всем трем разделам механики; по ним проходит единое соревнование.

Вданном пособии собраны наиболее интересные задачи всех олимпиад ПГТУ (ППИ) за 1974–2009 гг. Некоторые задачи заимствованы из [1–19]. В ряде случаев заимствовалась только идея, а со-

4

держание задачи подвергалось существенной переработке. Задачи сгруппированы по темам и снабжены решениями; поиск решений, отличных от приведенных, может составить дополнительное задание для читателя.

Авторы надеются, что пособие будет полезно для студентов всех специальностей при подготовке к олимпиадам (разных уровней) и при углубленном изучении курса теоретической механики. Преподаватели же теоретической механики и общей физики могут найти в пособии задачи для практических занятий.

Предисловие ко второму изданию

Первое издание «Избранных задач», вышедшее в 2010 г., почти полностью разошлось среди студентов и преподавателей ПНИПУ и других вузов. Второе издание выходит к 40-летию студенческих олимпиад ПНИПУ (ПГТУ, ППИ) по теоретической механике. За эти годы в них приняли участие около 5100 студентов. В мае 2012 г. прошла 50-я олимпиада (с 2000 г. ежегодно проводятся две олимпиады). Во втором издании количество задач увеличено вдвое (их стало 142), причем, в соответствии с традицией ряда олимпиадных сборников, к задачам с нечетными номерами приведены подробные решения, а к задачам с четными номерами – только ответы. Исправлено несколько неточностей; расширен список литературы. Все задачи имеют «студенческий» уровень сложности, но авторы надеются, что и специалисты по теоретической механике могут найти в сборнике новые идеи. Например, задача С5 побуждает задуматься о точной формулировке закона Кулона.

Авторы благодарны рецензентам П.В. Трусову и С.В. Лутманову за внимательное рецензирование рукописи.

5

Задачи

¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯

СТАТИКА

Статика твердого тела

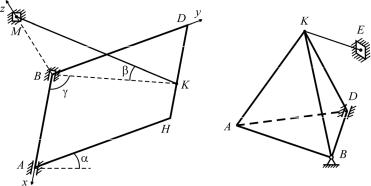
С1 (1980). Однородная прямоугольная плита ABDH массой m удерживается в равновесии тросом KМ, подшипником A и подпятником B. Плита образует угол с горизонтом и прямой угол с отрезком BM; положение троса задано углами и ; DK k DH ,

где k – заданный коэффициент.

Найти реакции y A , z A , xB , yB , zB подшипника A и подпятника B и модуль T силы натяжения троса.

С2 (2009). Однородный правильный тетраэдр ABDK массой m удерживается в равновесии сферическим шарниром B, цилиндрическим шарниром D и нитью KE, параллельной ребру AB. Основание ABD горизонтально.

Найти модуль T силы натяжения нити.

С3 (1981). Однородный брус массой m, имеющий форму прямоугольного параллелепипеда, может вращаться без трения вокруг неподвижной оси AB. Брус удерживается в равновесии тросом DK.

Найти модуль T силы натяжения троса.

6

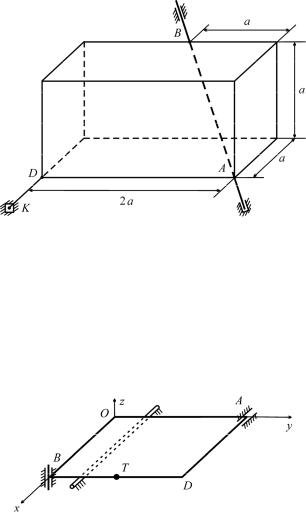
К задаче С3

С4 (2010). Однородная квадратная плита OADB массой M удерживается в равновесии цилиндрическими шарнирами A, B и неподвижным тонким гладким стержнем, на который она опирается по всей своей ширине. К краю плиты прикреплена тяжелая точка T. Длина каждой стороны плиты равна ; стержень параллелен сторо-

не OB и находится на расстоянии 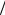4 от нее; расстояние BT 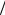2 .

Найти, при каких значениях m массы точки T такое равновесие возможно.

К задаче С4

С5 (1983). Однородный тяжелый стержень OA укреплен на сферическом шарнире в точке O и опирается на неподвижную вертикальную шероховатую плоскость. Коэффициент трения между

7

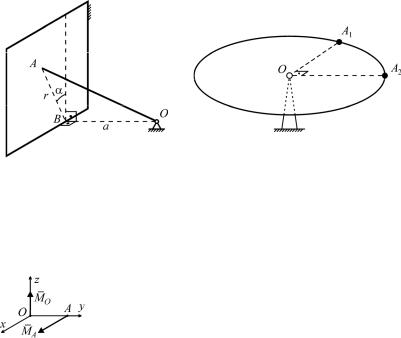
стержнем и плоскостью равен f. Расстояния OB a и BA r известны.

Найти, при каких значениях угла 0 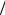2 стержень может находиться в равновесии.

С6 (2011). Круглая невесомая пластина закреплена в центре O сферическим шарниром. К краю пластины прикреплены материаль-

ные точки A1 и A2 массами m и 2m соответственно. Угол A1OA2 –

прямой.

Найти минимальную величину F силы, которую следует приложить к пластине в какой-либо точке, чтобы удержать пластину в равновесии в горизонтальном положении.

С7 (1992). На твердое тело действует система сил, главные моменты которой относительно точек O и A отличны от нуля и направлены так, как показано на рисунке.

Доказать, что такая система сил не имеет равнодействующей.

сти диска пара сил с моментом M.

8

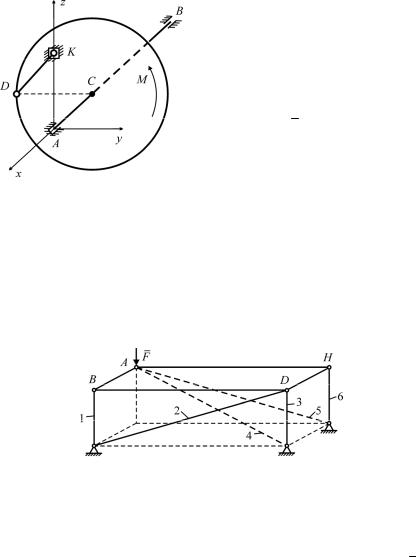
Найти модуль RA реакции в шарнире A.

С9 (1993). Прямоугольная однородная плита ABDH массы m удерживается в равновесии шестью стержнями, массами которых пренебречь. На плиту действует верти-

кальная сила F .

Доказать, что усилия в стержнях не зависят от размеров конст-

К задаче С9

С11 (1996). Однородный стержень AB массы m опирается концом A на шероховатую вертикальную плоскость (коэффициент трения равен f ), а концом B – на гладкую горизонтальную плоскость.

К точке B приложена заданная постоянная горизонтальная сила F . Найти область значений угла 0 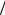2 , при которых воз-

можно равновесие стержня.

9

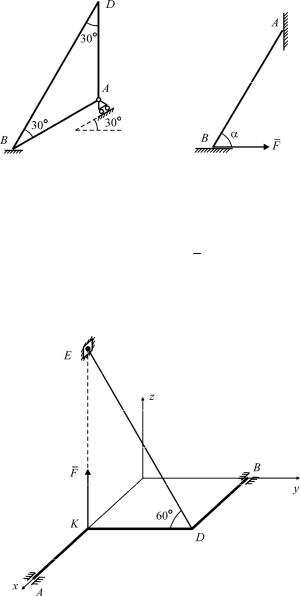
К задаче С10 К задаче С11

С12 (2013). Изогнутый под прямыми углами невесомый стержень AKDB закреплен в цилиндрических шарнирах A и B . В точке D к стержню привязана нить DE . В точке K на стержень дей-

ствует заданная вертикальная сила F . Расстояния AK KDDB . Стержень находится в равновесии.

Найти составляющую yB реакции в шарнире B.

К задаче С12

10