Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Тестовый контроль по математике учебно-методическое пособие

..pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

1.69 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 124 5 6 7 8 9 10 11 12 > Следующая >>>

2a − 3a +

a = 0; −6 + 9 −

;8 −12 + 2 =

; −2 .

Ответ:

2a − 3a +

a = 0;

; −2 .

Пример 9

b = {1;0;1} равен…

Угол между векторами a = {1;1;0}

1)* 60°;

2) 30°;

3) 15°;

4) 45°.

Решение. Обозначим угол между векторами a и b через ϕ .

cos φ =

b )

1 1 +1 0 + 0 1

+12 + 02 12 + 02 +12

2 2

Следовательно, φ = 60°.

Ответ: φ = 60°.

Пример 10

Векторы a = {2;5;7} ,

b = {1;1; −1} , c = {1; 2; 2}

являются…

1)* компланарными;

2) коллинеарными;

3) взаимно перпендикулярными;

4) равными по длине.

Решение. Вычислим смешанное произведение векторов

a,b , c :

a b c =

1 −1

−1

1 1

1 1 −1

= 2

− 5

+ 7

= 2(2 + 2

) − 5(2 +1

) + 7 (2 −1) = 8 −15 + 7 = 0.

Так как смешанное произведение векторов a, b

и c равно

нулю, то они компланарны.

Возможны ошибки:

1. Так как координаты векторов не пропорциональны, то векторы не коллинеарны.

2. Так как (a c ) = 2 1 + 5 2 + 7 2 = 26 ≠ 0, то векторы a, b

и c не являются взаимно перпендикулярными.

4 + 25

49 = 78 ,

1 +1 +1 =

3 ,

1 + 4 +

9 = 3 , следовательно, векторы не рав-

ны по длине.

Ответ: a,b и с компланарны.

Пример 11

Работа по перемещению материальной точки из точки

M1 (1; −1; 2)	в точку M 2 (3; −2;0)			под воздействием силы
f = {3; −5; 2}	равна…
1)* 7;	2) 17;	3) –7;	4) 3 38.
Решение. Найдем вектор				перемещения s = M1M 2 =
= {3 −1; − 2 − (−1); 0 − 2} = {2;−1;−2} .
Вычислим работу:

A = ( f s ) = 3 2 + (−5) (−1) + 2 (−2) = 6 + 5 − 4 = 7.

Ответ: A = 7.

Возможны ошибки:

Вычислять скалярное произведение по определению в данном случае не рационально.

Примеры второго уровня сложности

Пример 12

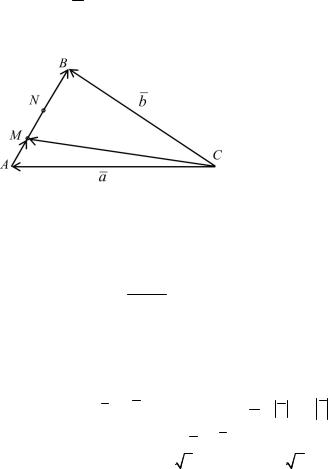
Дан треугольник с вершинами	А, В и С. Сторону АВ
точками MN разделили на три равные	части. CA = a,CB = b.
Вектор CM равен…
32

1)*

+ b

;

b − 2a

; 3)

2a − b

;

a + b

Решение:

Поправилутреугольника

= CB − CA = b −

Так как по условию

то AM =

AB =

b − a

По

правилу

треугольника

сложения

двух

векторов

CM = CA + AM = a +

b − a

2a + b

Ответ: CM = 2a + b . 3

Возможны ошибки при применении правила сложения векторов.

Пример 13

Векторы a и b образуют угол π, a = 3, b = 4 , скаляр- 3

ное произведение векторов ( 3a − 2b ) и ( a + 2b ) равно…

1)* –13; 2) −37 + 6 3; 3) −37 + 6 2; 4) –31.

Решение. Посвойствам скалярного произведениявычислим

(3a − 2b ) (a + 2b ) = 3(a a ) + 6(a b ) − 2(b a ) − 4(b b ) =

= 3

2 + 4

cos

− 4

2 = 3 9 + 4 3 4

− 4 16 = −13.

Ответ: –13.

Возможны ошибки:

Раскрывая скобки, надо помнить, что каждое слагаемое является скалярным произведением векторов.

Пример 14

Угол φ между векторами a и b равен π, a = 2; b = 3.

Длина векторного произведения векторов (a + b ) и (2a − 3b ) равна…

1)* 21 3 ; 2) –40; 3) 12; 4) 42.

Решение:

По свойствам векторного произведения вычислим

(a + 2b )× (2a− 3b )= a× 2a− a× 3+b 2×b 2−a ×2b =3b

= 2a × a− 3a× b− 4a× −b 6×b =b− ×7a b.

Вычислимдлину векторного произведенияпо определению:

(a + 2b )×

(2a− 3b )

= − 7a× b= 7

a× b=

sin=φ

= 7 2 3

= 21 3.

Ответ: 21

Возможны ошибки:

Следует помнить, что векторное произведение не коммутативно: a × b= − b× a.

Пример 15

Сила p = {2; −4;5} приложена к точке M 0 (4; −2;3). Момент этой силы относительно точки A(3;2; −1) равен…

1)* {−4;3;4} ; 2) {−4;−3;4} ; 3) {4; −3;−4} ; 4) {4;3;4} .

Решение. Момент силы p,

приложенной к точке М0 относительно точки A, как известно из механики, вычисляется по формуле

M = AM 0 × p.

1) Найдем координаты вектора AM 0 : AM 0 = {1; −4; 4} .

2) Вычислим векторное произведение векторов AM 0 и p :

i j k

M = AM 0 × p= 1− 4 4 = i (− 20+ 16)− j (5− 8)+ k (− 4+ 8)=

2 − 4 5

= −4i + 3 j + 4k .

Ответ: M = {−4;3; 4}.

Возможны ошибки:

Если переставить в определителе строки, то знак изменится на противоположный, то есть получим вектор −M .

Пример 16
Объем			треугольной пирамиды с вершинами в точках
А (2; 2; 2), В (4; 3; 3), С (4; 5; 4), Д (5; 5; 6) равен…
1)*	7	;	2) 7;	3) ±7 ;	4) 42.

6

Решение:

1) Найдем координаты векторов АВ, АС, АД : АВ = {2;1;1} ,

АС = {2;3; 2} , АД = {3;3; 4}.

2) Смешанное произведение векторов вычисляется по формуле

			xa		ya		za
	abc =		xb		yb		zb		.
			xc		yc		zc
Тогда
АВ АС АД =	2	1	1	= 2		3	2	−		2	2	+	2	3	=


	2	3	2
	3	3	4			3	4			3	4		3	3
	3	3	4

= 2(12 − 6) − (8 − 6) + (6 − 9) = 12 − 2 − 3 = 7.

Объем пирамиды V = ± 1 abc = 7 . (Знак «–» берется в том

6 6

случае, если смешанное произведение векторов отрицательно.)

Ответ: V = 7 . 6

Пример 17
Проекция вектора s = {4; −3; 2}			на ось u, составляющую
с координатными осями равные углы, равна…
1)* 3;	2) 4, − 3, 2;	3)	29;	4)	1	.

				3
Решение. Для вычисления проекции вектора s на ось u
воспользуемся формулой
	прu s = x cos α+ y cosβ+ z cos γ,
где s = {x, y, z} ,	cos α, cosβ,	cos γ –	направляющие косинусы

оси u, e = {cos α,cosβ,cos γ} – вектор единичной длины, параллельный оси u. По условию ось u составляет с осями коорди-

нат равные углы, то	есть α = β = γ.	Тогда из условия
cos2α+ cos2 β+ cos2 γ =1	следует, что	3cos2α =1,	или

cos α = ± 1 . Выберем положительное направление вектора e,

3
тогда e =	1	;	1	;	1	и прu s = 4	1	− 3	1	+ 2	1	= 3.
	3		3		3		3
								3		3
Ответ:			3 .

Возможны ошибки:

Координаты вектора s = {4; −3;2} являются проекциями вектора s на оси координат, но не на ось u.

Пример третьего уровня сложности

Пример 18

Даны три вектора: l = {3; −2;1} , p = {−1;1;−2} , q = {2;1;−3} .

Разложение вектора c = {11; − 6; 5} по базису l , p, q имеет вид…

1)*

= 2l − 3

+ q ;

= l − 3

+ q ;

= 2l + 3

+ q ;

= 2l − 3

+ 3q.

Решение. Разложением вектора c = {x4 ; y4 ; z4 } по базису

l = {x1; y1; z1} , p = {x2 ; y2 ; z2 }

и q = {x3 ; y3 ; z3 }

называется линей-

ная комбинация векторов

c = αl + βp + γq ,

при условии, что

l , p и q не компланарны и не являются нулевым. По правилу вычисления координат должны выполнятся условия

αx1 + βx2 + γx3 = x4 ,αy1 + βy2 + γy3 = y4 ,αz1 + βz2 + γz3 = z4 .

Для данных по условию векторов система имеет вид

3α− β+ 2γ =11,

−2α+ β+ γ = −6,

α− β− γ =

2 3 5.

Решая систему методом Крамера, получим α = 2;

β = −3; γ = 1.

Искомое разложение имеет вид: c = 2l − 3 p + q.

Ответ: c = 2l − 3 p + q.

Возможны ошибки при составлении и решении системы уравнений.

Пример 19

Даны три точки A(1;1;1) , B (2; 2; 2), C (4; 3; 5) . Площадь треугольника ABC в кв. ед. равна…

1)*

;

4) 2.

Решение:

1) Найдем координаты векторов

AB и AC по формуле

AB = {xB − xA ; yB − yA

; zB − zA } :

AB = {2 −1; 2 −1; 2 −1} = {1;1;1}

AC = {4 −1;3 −1;5 −1} = {3; 2; 4}.

2) Векторное

произведение векторов вычисляется по

формуле

a × b=

Тогда векторное произведение векторов AB и AC

AB × AC=

= i

1 1

− j

1 1

+ k

1 1

1 1 1

3 2 4

2 4

3 4

3 2

= i (4 − 2) − j (4 − 3) + k (2 − 3) = 2i − j − k .

Таким образом, AB × AC= {2;− 1;− 1} .

3) Вычислим длину векторного произведения: AB × AC =

= 22 + (−1)2 + (−1)2 = 4 +1+1 = 6.

4) Площадь треугольника равна половине произведения сторон на синус угла между ними, с другой стороны, длина векторного произведения равна произведению длин векторов на синус угла между ними, поэтому площадьтреугольникаABC (кв. ед.)

S∆	=	1		AB	AC	sin α =	1	AB × AC	=	6	.
		1					1			6

	2					2				2
Ответ:	6		.
Ответ:			.
	2

Тест по разделам «Линейная алгебра» и «Векторная алгебра»

Время прохождения – 60 мин. Задания 1-го уровня сложности: 1–18; задания 2-го уровня сложности: 19–27; задания 3-го уровня сложности: 28–30.

Оценка «удовлетворительно» ставится за 16–21 правильно решенных заданий;

оценка «хорошо» ставится за 22–27 правильно решенных заданий;

оценка «отлично» ставится за 28–30 правильно решенных заданий.

1. Если A = 1			2	и	B = 0	3 , то 2A + B равно…
		4	5		2	−1
1) 12	−7	;	2) 2		7 ;	3) −12	−7	;	4) 0	7 .
10	9			10	9	10	9		10	9

															2	1
2. Произведение					матриц			A = (2		1	3)	и	B =		3	0
														−1		4
равно…												1
1) −4	14 ;	2) 4 ;										1
1) −4	14 ;	2) 4 ;						3) (4 14);				4)	4 .
2	0				14							2
												2
3. Матрица, транспонированная к матрице												A = 2			3	5 ,
													1	−2		0
имеет вид…										2		3		2		1
1) 1	−2 0	; 2) 3 2						5 ; 3)		2		3		2		1
1) 1	−2 0	; 2) 3 2						5 ; 3)			5	0 ; 4)		3	−2 .
2	3 5				−2 1 0					1		2		5		0
										1		2		5		0
4. Определитель				2		−1	равен нулю при λ, равном…
4. Определитель				2		−1	равен нулю при λ, равном…
				λ		3
1) –6;	2) 6;		3) 3;					4) 12.
					1	2		3
					1	2		3
5. Определитель					0	−1		4	равен…
					−2	−3		5
1) 15;	2) –15;					3) 10;			4) –12.
														1	2	3
6. Алгебраическое дополнение А21 матрицы A =														−1	2	0
														4	1	5
равно…
1) –7;	2) 7;		3) 10;					4) –10.

<<< < Предыдущая 1 2 34 / 124 5 6 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.2022548.89 Кб3Теория электропривода..pdf
#
15.11.2022548.89 Кб3Теория электропривода.pdf
#
15.11.20224.77 Mб38Теплопередача учебное пособие..pdf
#
15.11.202210.8 Mб12Теплофизика в металлургии..pdf
#
15.11.20227.09 Mб13Теплофизические явления в полимерных материалах при интенсивном и кр..pdf
#
15.11.20221.69 Mб11Тестовый контроль по математике учебно-методическое пособие..pdf
#
15.11.202210.87 Mб21Техника технология и технические средства применяемые при реконстру..pdf
#
15.11.20221.1 Mб11Техника высоких напряжений..pdf
#
15.11.202212.64 Mб140Техника и технология капитального ремонта скважин..pdf
#
15.11.20227.28 Mб12Техника разведки лабораторный практикум..pdf
#
15.11.20229.09 Mб17Технические измерения и приборы..pdf