5561

УДК 517.9 ББК В 1

Т 45

Тиунчик М. Ф. Практикум по дифференциальным уравнениям : учеб. пособие / М. Ф. Тиунчик, Ю. Г. Саяпина. – Хабаровск : РИЦ ХГАЭП, 2010. – 92 с.

Рецензенты: Е. Г. Агапова, канд. физ.-мат. наук, доцент кафедры прикладной математики ТОГУ; А. И. Ивлева, канд. физ.-мат. наук, доцент Хабаровского пограничного

института Федеральной службы Российской Федерации

Утверждено издательско-библиотечным советом академии в качестве учебного пособия

©Тиунчик М. Ф., Саяпина Ю. Г., 2010

©Хабаровская государственная академия экономики и права, 2010

2

Введение

Дифференциальные уравнения как самостоятельная дисциплина на современном этапе является наукой, имеющей разнообразные приложения как в самой математике, так и в физике, химии, экономических, социологических науках. Большинство вопросов сводятся к следующей задаче: найти функцию у, имея некоторое уравнение, в которое, кроме этой функции и аргументов, от которых она зависит, входят также её производные до некоторого порядка. Если искомая функция при этом зависит лишь от одного аргумента, такое уравнение называют обыкновенным дифференциальным уравнением.

Для основных экономических специальностей обыкновенные дифференциальные уравнения изучаются как раздел в общем курсе математики. Настоящее учебное пособие содержит весь материал, предусмотренный по данному разделу соответствующими государственными стандартами. Кроме того, оно может быть использовано студентами специальности «Математические методы в экономике», которые изучают дифференциальные уравнения отдельной дисциплиной.

В учебном пособии приведены основные теоретические сведения по теории обыкновенных дифференциальных уравнений первого и второго порядков. Рассмотрена тема «Системы линейных дифференциальных уравнений первого порядка в нормальной форме». Приведены задачи на составление и решение дифференциальных уравнений, в основном экономического содержания. Весь материал иллюстрируется примерами.

Авторами составлены тридцать вариантов индивидуальных заданий. Каждое типовое задание состоит из десяти упражнений. Вариант в полном объёме выдаётся студентам специальности «Математические методы в экономике». Для остальных специальностей вариант выдаётся не в полном объёме, а только по тем темам раздела, изучение которых предусмотрено соответствующим стандартом в общем курсе математики.

3

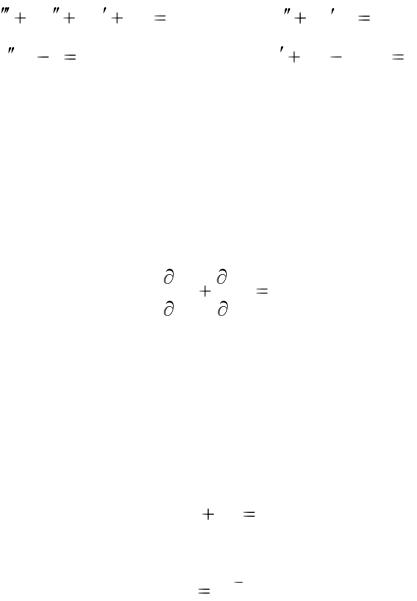
Общие понятия о дифференциальных уравнениях

Уравнение, в которое входят производные неизвестной функции, называется дифференциальным. Если эта искомая функция зависит лишь от одного аргумента, то уравнение называется обыкновенным дифференциальным уравнением. Если же неизвестная функция является функцией нескольких независимых переменных, то дифференциальное уравнение называется уравнением в частных производных.

Порядком дифференциального уравнения называется максимальный

(наивысший) порядок входящей в него производной неизвестной функции. Примерами обыкновенных дифференциальных уравнений являются

уравнения с неизвестной функцией у = у(х) :

При этом первое из них – третьего порядка, второе и третье – второго порядка, а четвёртое – первого порядка. Из примеров видно, что сама функция и некоторые её производные в записи уравнения могут отсутствовать (см. примеры 2 и 3), но обязательно наличие старшей производной при указанном порядке уравнения.

Примером дифференциального уравнения в частных производных является уравнение второго порядка

с неизвестной функцией y = y(x1, x2) двух переменных.

Решением дифференциального уравнения называется любая функция,

при подстановке которой в уравнение (с учётом входящих в него производных) получится тождество.

Например, решением обыкновенного дифференциального уравнения первого порядка

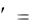
где с – произвольная постоянная. Таким образом, это уравнение имеет бесконечное множество решений.

В дальнейшем здесь будут рассматриваться только обыкновенные дифференциальные уравнения.

1 Дифференциальные уравнения первого порядка

Общий вид дифференциального уравнения первого порядка

представляет собой

Вравенстве (1.1) F есть известная функция трёх переменных, т.е. это соотношение связывает три переменные величины: независимую переменную х, неизвестную функцию у(х) и её производную y′(х).

Внекоторых случаях уравнение (1.1) можно однозначно разрешить относительно производной у′, т.е. представить в виде

дифференциальным уравнением первого порядка, разрешённым относительно производной.

Это уравнение, как и (1.1), рассматривают на некотором промежутке изменения аргумента х; например, на отрезке [a, b]. Часто эти уравнения рассматриваются на множестве (–∞, +∞), т.е. на всей координатной прямой Ох.

Уравнение (1.2) более доступно для изучения, чем дифференциальное уравнение общего вида (1.1). Так, воспользовавшись равенством dy = y′dx, его можно представить в виде

где P и Q – конкретные функции двух переменных.

Уравнение (1.4) будем называть дифференциальным уравнением первого порядка, записанным в дифференциальной форме.

Самым простым примером дифференциального уравнения вида (1.2) является уравнение

у′ = f(x),

5

где f(x) – известная функция.

Из интегрального исчисления известно, что решение находится интегрированием этой функции:

y = 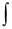f (x)dx = F(x) + C,

где С – произвольная постоянная, а F(x) – одна из первообразных функций для функции f(x). Следовательно, дифференциальное уравнение такого вида имеет бесконечное множество решений.

Например, решением уравнения у′ = 2х является множество у = х2 + С, т.е. геометрически представляет собой семейство парабол в прямоугольной декартовой системе координат Оху. Каждую такую функцию называют

исчисления, уже не выражаются через элементарные функции. Всё же те уравнения, решения которых выражаются через интегралы от элементарных функций, принято называть разрешимыми «в квадратурах». Этот термин возник в связи с тем, что операция интегрирования связана с отысканием площадей фигур.

Процесс нахождения решения дифференциального уравнения первого порядка, связанный с операцией интегрирования, принято называть

интегрированием дифференциального уравнения.

Выделим во множестве решений y=x2 + C только что рассмотренного дифференциального уравнения y′ = 2x функцию (интегральную кривую), проходящую через точку М(1, 2), т.е. решение, удовлетворяющее условию у(1) = 2. Им будет интегральная кривая у = х2 + 1. Такое решение называется частным решением (частным интегралом) этого дифференциального уравнения. Оно получилось из решения у = х2 + С подбором постоянной С (в данной ситуации оказалось, что С = 1). В дальнейшем решение у = х2 + С, где С – произвольная постоянная, будет называться общим решением (общим интегралом)

уравнения y′ = 2x. С геометрической точки зрения общее решение представляет собой семейство интегральных кривых (в данном случае – семейство парабол).

Всякое решение дифференциального уравнения (1.1) или (1.2) при условии

6

где х0 – произвольная точка из промежутка, на котором рассматривается уравнение, а у0 – произвольно заданное число, называется частным решением

(частным интегралом) дифференциального уравнения. График частного решения называют интегральной кривой.

Равенство (1.5) называется начальным условием для дифференциального уравнения.

Геометрически оно означает, что на плоскости Оху задаётся точка М0(х0, у0), через которую должна проходить искомая интегральная кривая, т.е. график функции у = у(х).

Задача нахождения решения дифференциального уравнения (1.1) или (1.2) с присоединённым к нему условием (1.5), называется задачей Коши или

задачей с начальным условием.

Непрерывно дифференцируемая функция (функция, непрерывная вместе с её производной)

которая содержит одну произвольную постоянную С, называется общим решением дифференциального уравнения или общим интегралом (1.1) или

(1.2), если выполняются следующие два условия:

1)при каждом фиксированном С эта функция является решением соответствующего уравнения;

2)каково бы ни было начальное условие (1.5), найдётся такое конкретное число С, что функция (1.6) при этом С будет удовлетворять этому условию.

Запись (1.6) означает, что имеется явная форма общего решения

(общего интеграла).

Однако во многих случаях при решении дифференциального уравнения удаётся получить лишь неявное выражение общего решения (общего интеграла)

т.е. некоторое соотношение, связывающее аргумент х, неизвестную функцию у = у(х) и содержащее одну произвольную постоянную С.

Таким образом, общее решение дифференциального уравнения первого порядка есть решение, из которого путём подбора постоянной С можно получить частное решение с любым подходящим этому уравнению начальным условием.

Сформулируем теорему о существовании и единственности решения дифференциального уравнения (1.2) с начальным условием (1.5).

7

Пусть правая часть f(x,y) уравнения (1.2) как функция двух переменных х, у удовлетворяет следующим условиям:

1) непрерывна в некоторой области D на плоскости, содержащей точку (х0, у0), являющуюся внутренней для D;

2) функция f имеет непрерывную частную производную по переменной у в области D. Тогда найдётся такое число δ > 0, что на отрезке [x0 – δ, x0 + δ] из промежутка, на котором рассматривается дифференциальное уравнение, решение задачи Коши (1.2), (1.5) существует и единственно.

Обычно х (– ∞, + ∞). Но если х принадлежит некоторому отрезку [a, b], то область D на плоскости предполагается такой, что точка х0 является

2 Дифференциальные уравнения с разделёнными и разделяющимися переменными

Дифференциальным уравнением с разделёнными переменными

которое записано в дифференциальной форме. Здесь f1(y), f2(x) – известные непрерывные функции своих аргументов. Переменные х и у разделены, поскольку в уравнении (2.1) левая часть содержит лишь переменную у и её дифференциал, а правая часть – только переменную х и её дифференциал.

Соотношение вида

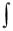f1 ( y)dy 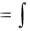f2 (x)dx C (2.2)

является общим интегралом дифференциального уравнения с разделёнными переменными.

Пример. Найти решение дифференциального уравнения

Тогда у = ( – 0,5cos x + 0,5C)2.

Дифференциальным уравнением с разделяющимися переменными

называется уравнение вида

Интегрируя это равенство, получим следующее:

9

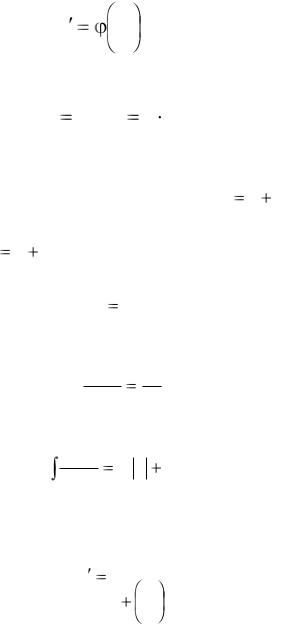
3 Однородные дифференциальные уравнения

Функция f(x, y) называется однородной функцией нулевой степени, если для любого t ≠ 0 выполняется равенство

уравнением первого порядка, если f(x, y) есть однородная функция нулевой степени.

Тогда уравнение (1.2) можно привести к виду

где Ф(u) = φ(u) – u. Переменные разделяются: du dx .

Ф(u) x

Общее решение «в квадратурах» выглядит следующим образом:

где С – произвольная постоянная (С > 0).

Пример. Найти решение дифференциального уравнения

10