Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Хабаровский государственный университет экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5561

.pdf

Скачиваний:

Добавлен:

13.11.2022

Размер:

1.87 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 106 7 8 9 10 > Следующая >>>

x1	t	Re	e	kt	,	x2	t		e	kt	.
y1 t						y2	t	Im

Это означает, что из комплексного решения

x t	x1 t	ix2	t ,
y t	y1 t	iy2	t ,

соответствующего комплексному корню a + bi характеристического уравнения системы, выделены пары действительных решений

x1 t	Re x t , x2 t	Im x t ,
y1 t	Re y t , y2 t
y1 t	Re y t , y2 t	Im y t

действительная и мнимая части комплексного решения, которые образуют фундаментальную систему решений. Комплексно-сопряжённый корень a – bi характеристического уравнения задаёт эту же фундаментальную систему решений.

Пример 2. Найти общее решение системы дифференциальных уравнений

	dx		4x 3y,

	dt
	dt
	dy		3x 4 y.

	dt
	dt

Решение. Характеристическое уравнение данной системы имеет вид:

	4 k	3	0 или k 2		8k	25	0 .
	3	4 k	0 или k 2		8k	25	0 .
	3	4 k
Корни этого уравнения таковы: k1,2			4 3i . Найдём решение системы (11.3),
отвечающее одному из этих корней,			например,		k1	4	3i . В данном примере
система (11.3) в случае этого корня имеет вид
4		4	3i	3	0,
3		4	4	3i		0.
После упрощения получаем систему
		3i	3	0,
		3	3i	0,

которая имеет бесчисленное множество ненулевых решений. Одним из этих

решений является вектор	,	= 1,	i .
Подставим корень	k1	4	3i и полученные	1,	i в (11.2).
Получим решение данной системы как комплексные функции
			51

x t e 4 3i t ,

y t 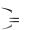ie 4 3i t .

Действительная и мнимая части этого решения также являются решениями рассматриваемой системы. Для выделения этих частей воспользуемся равенством

e yi

и формулой Эйлера

e yi

cos y

i sin y.

Тогда получим, что

x t

cos3t

i sin 3t ,

y t

i(cos3t

i sin 3t)

sin 3t i cos3t .

Таким образом,

Re x t

cos3t ,

Re y t

sin 3t ,

Im x t

Im y t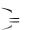 e 4t cos3t .

Действительные линейно независимые решения задаются функциями:

x1 t e x2 t e

cos3t, y1 t e 4t sin 3t ; sin 3t, y2 t 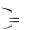e 4t cos3t.

Эти решения и образуют фундаментальную систему. Общее решение данной системы уравнений таково:

x t	e	4t (С cos 3t	С	2	sin 3t ),
		1		2
y t	e	4t (С sin 3t	C	2	cos 3t),
		1		2

где C1,C2 – произвольные постоянные.

Построение фундаментальной системы решений системы линейных дифференциальных уравнений в случае кратных собственных чисел матрицы системы уравнений является значительно более сложной задачей. Разберём эту ситуацию на примере.

Пример 3. Найти общее решение системы дифференциальных уравнений

dx	2x	y,

dt
dt
dy	x	4 y.

dt
dt

Решение. Характеристическое уравнение этой системы таково:

2 k	1	0 или k 2	6k 9 0 .
1	4 k	0 или k 2	6k 9 0 .
1	4 k

Оно имеет один двукратный корень k=3 (k1=k2=3). Решение системы надо искать в виде

			x	1		t e3t ,
				1		1
			y	2		2t e3t .
Продифференцировав эти функции, получим
	dx			e3t	3		3 t e3t ,
		1				1

	dt						1
	dt
	dy		2e3t		3 2		3 2t e3t .

	dt
	dt
Подставляя эти функции x t ,				y t	и их		производные в данную систему,

сокращая на e3t , получим следующие равенства:

1	3 1t 2 1		2 1t	2	2 2t,
2	3 2t	1	1t	4 2	4 2t.

Левые и правые части этих равенств являются многочленами первой степени относительно переменной t. Приравнивая соответствующие коэффициенты этих многочленов, получим следующую систему из четырёх линейных

алгебраических уравнений с четырьмя неизвестными						1, 1, 2 , 2 :
1	3 1	2 1	2 , 3 1		2 1	2 ,
2	3 2	1	4 2 , 3 2		1	4 2 .
После преобразований получаем систему
	1	1	2 ,	1	2 ,
	2	1	2 ,	1	2 ,

ранг которой равен двум и свободных неизвестных – две. В качестве двух линейно независимых уравнений можно взять, например,

					1	2 , 1	2	2.
Очевидно,			что	за	базисные	переменные		можно взять	1, 1; тогда
2 ,	2	свободные переменные,				которые остаются произвольными. Обозначив
эти	произвольные				постоянные,	соответственно, через С1 и			С2, получим,
что	1	С1	С2 ,	1	С2 . Итак, общее решение рассматриваемой системы таково:

x t 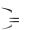C1 C2 C2t e3t , y(t) 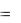C1 C2t e3t .

Сделаем замечание по поводу вида, в котором ищется общее решение системы уравнений примера 3 (случай, когда характеристическое уравнение системы имеет двукратный действительный корень).

Эту систему можно свести к решению линейного дифференциального уравнения второго порядка с постоянными коэффициентами относительно одной из неизвестных функций. Сделаем это. Продифференцируем второе

уравнение; получим, что

d 2 y

. Подставим в это уравнение

из

dt 2

первого уравнения исходной системы.

Получим, что

d 2 y

2x y 4

. В

это уравнение подставим функцию x, найденную из второго уравнения исходной системы ( x 4 y dydt ). Окончательно имеем следующее уравнение с неизвестной функцией y(t):

d 2 y	6	dy	9 y 0.
dt 2		dt

Это есть линейное однородное дифференциальное уравнение второго порядка с

постоянными

коэффициентами,

характеристическое

уравнение

которого

k 2

9 0 совпадает с характеристическим уравнением системы примера 3.

Функции

e3t ,

te3t

задают фундаментальную

систему

уравнения

общим

решением

которого

является

функция

t e3t (см.

тему

7). Как видно, оно совпадает с решением y t

системы этого примера.

Изучим ещё систему трёх уравнений с тремя неизвестными функциями

x t

, y t

, z t

вещественной переменной t

a11x

a12 y

a13 z,

a21x

a22 y

a23 z,

(11.7)

a31x

a32 y

a33 z,

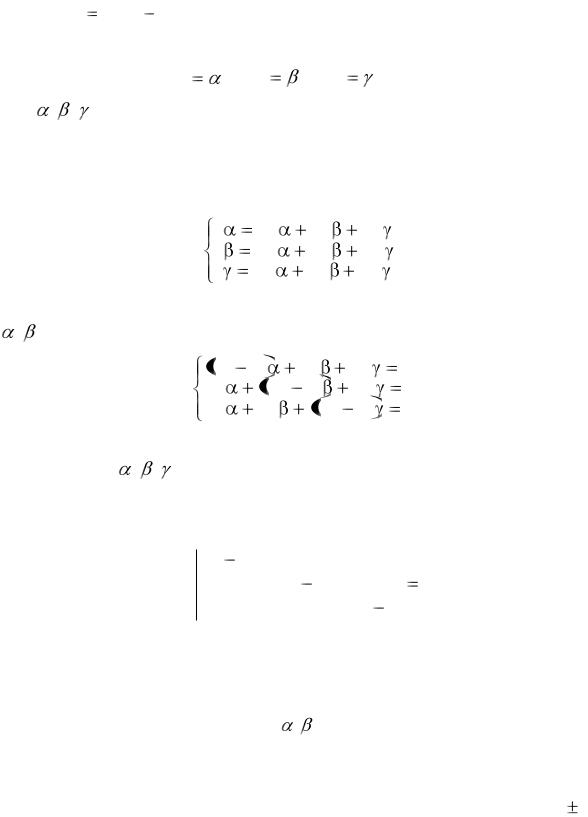
где asj (s, j	1,2,3)	постоянные действительные числа.
Будем искать частное решение системы в следующем виде:
		x	ekt ,	y	ekt , z	ekt ,	(11.8)
где , ,	и k –	некоторые		числа,	которые	надо определить так,	чтобы

функции (11.8) были решением системы (11.7).

Подставляя данные функции и их производные в уравнения системы и сокращая на ekt , получим

k	a11	a12	a13	,
k	a21	a22	a23	,
k	a31	a32	a33 .

Перенося все члены в одну часть равенства и группируя коэффициенты при

, , , получим систему уравнений

	a11	k	a12	a13	0,
	a21	a22	k	a23	0,	(11.9)
	a31	a32	a33	k	0.
Система (11.9) есть система трёх уравнений первой степени с тремя
неизвестными	, , . Как известно, чтобы эта				система имела	ненулевое

решение, необходимо и достаточно, чтобы её определитель был равен нулю, т. е. чтобы число k было корнем уравнения

a11 k	a12	a13
a21	a22 k	a23		0.	(11.10)
a31	a32	a33	k

Уравнение (11.10) называется характеристическим уравнением для системы (11.7). Оно является уравнением третьей степени относительно k и из него определяются те значения k , при которых система (11.9) имеет нетривиальные (ненулевые) решения , ,.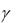

Из алгебры известно, что уравнение (11.10) будет иметь три корня с учётом их кратности. Комплексные корни всякого алгебраического уравнения с действительными коэффициентами являются сопряжёнными парами a bi . Поэтому уравнение (11.10) , являющееся уравнением нечётной степени (в данном случае третьей степени), будет иметь хотя бы один действительный корень k .

Таким образом, относительно корней уравнения (11.10) возможны следующие ситуации:

1) все корни k1, k2, k3 действительны и различны;

2)имеется пара комплексно-сопряжённых корней и один действительный корень;

3)корни действительны и один из них является двукратным;

4)один действительный трёхкратный корень.

Рассмотрим первую ситуацию, когда все корни k1, k2, k3 уравнения (11.10) действительны и различны, т.е. матрица системы имеет простой спектр. Подставляя их по очереди в систему (11.9), найдём конкретные собственные векторы

1, 1, 1 ,

2 , 2 , 2 ,

3 , 3 , 3 .

В результате получим фундаментальную систему решений исходной системы

(11.7):

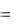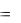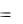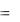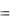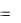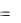x1 1ek1t , y1 1ek1t , z1 1ek1t ; x2 2ek2t , y2 2ek2t , z2 2ek2t ; x3 3ek3t , y3 3ek3t , z3 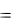3ek3t .

Общее решение системы (11.7) можно записать в виде

x t		1				2				3
		1				2				3
y t	C	1	ek1t	C	2	2	ek2t	C	3	3	ek3t ,	(11.11)
	1	1			2	2			3	3
z t		1				2				3
		1				2				3

где C1,C2 ,C3 – произвольные постоянные.

Пример 4. Найти общее решение системы дифференциальных уравнений

dx	3x	2 y	2z,

dt
dt
dy	4x	3y	4z,

dt
dt
dz	4x	2 y	3z.

dt
dt

Решение. Характеристическое уравнение для системы имеет вид

3 k	2	2
4	3 k	4		0.
4	2	3	k
	56

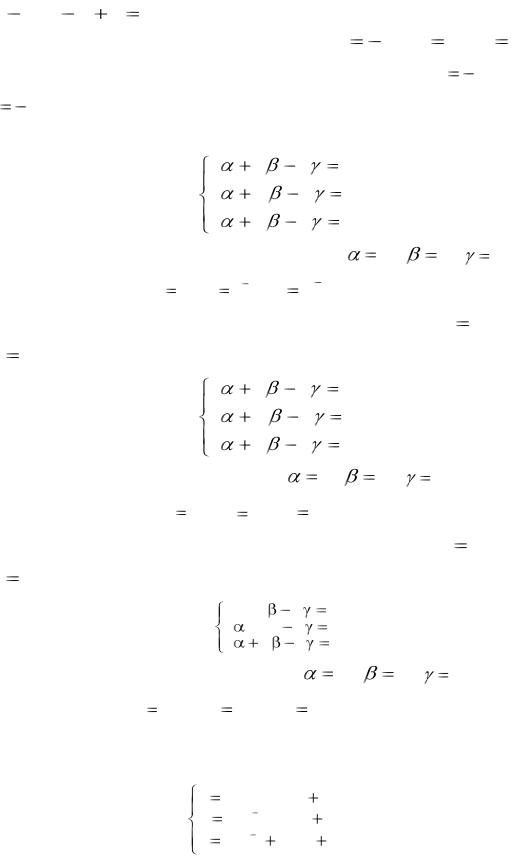
Вычислив		определитель,			получим					уравнение				третьей			степени
k 3	3k 2	k 3 0. Все корни							характеристического						уравнения –
действительные и различные числа, а именно:										k1			1, k2	1,	k3		3.
	Найдём частное решение, соответствующее корню													k1	1.	Подставляя
k1	1 в систему (11.9), получаем						следующую						алгебраическую				систему
уравнений:
				4		2			2		0,
				4		4			4		0,
				4		2			2		0.
Одним из решений этой системы будут числа:													0,	1,		1.	Согласно
(11.8) частное таково:			x	0, y	e	t , z			e t .
			1	1			1
	Найдём частное решение, соответствующее корню													k2	1.	Подставляя
k2	1 в систему (11.9), получаем:
				2		2			2		0,
				4		2			4		0,
				4		2			4		0.
Одно из решений этой системы таково:									1,				0 ,	1. Частное решение
имеет следующий вид:			x2	et , y2		0 ,	z2		et .
	Найдём частное решение, соответствующее корню													k3	3.	Подставляя
k3	3 в систему (11.9), получаем:
						2		2		0,
					4			4		0,
					4	2		6		0.
Одним из решений этой системы будет										1,			1,	1.	Тогда частное
решение имеет вид x3			e3t , y3		e3t , z3				e3t .
	Таким образом, найдена фундаментальная система решений.
	Общее решение исходной системы примера 4 таково:
				x		C2et				C3e3t ,
				y	C e t					C	e3t ,
					1					3
				z C e t			C		et	C		e3t ,
					1		2			3
где C1 , C2		и C3 – произвольные постоянные.
						57

Пример 5. Найти общее решение системы дифференциальных уравнений

dx	x	2 y	z,

dt
dt
dy	2x	3 y	3z,

dt
dt
dz	x	3 y	2z.

dt
dt

Решение. Характеристическое уравнение для этой системы таково:

			1 k	2		1
			2	3	k	3		0.
			1	3		2	k
Корнями	характеристического			уравнения		k 3 2k 2			k	2	0 являются
числа k1	i , k2	i и k3		2 . Один корень характеристического уравнения
– действительный, а два другие – комплексно-сопряжённые.
Найдём частное решение, соответствующее корню									k1	i .	Подставляем
корень k1	i в систему (11.9), получаем систему для отыскания неизвестных ,
и :
		1		i	2		0,
		2		3	i	3	0,
				3	2	i	0.

Эта система имеет множество решений. Возьмём значение

2 ,

тогда

1 i ,

i . Комплексное решение

начальной

системы

имеет

вид:

x eit 1

i , y

eit 1

i ,

2eit .

Используя

формулу Эйлера, запишем

полученное решение системы в виде

cost

i sin t

cost

sin t

i sin t

cost ,

cost

i sin t

cost

sin t

i sin t

cost ,

2(cost

i sin t).

Известно,

что действительная и мнимая части полученного решения по

отдельности представляют собой решение исходной системы. Таким образом, имеем два действительных решения исходной системы:

x1	cost sin t,	y1	cost	sin t , z1	2 cos t ;
x2	sin t cost,	y2	sin t	cost , z2	2sin t .
Найдём частное решение,		соответствующее корню k3 2 . Подставляем

k3 2 в систему (11.9), получаем:

2		0,
2	3	0,
3	4	0.
Одно из решений этой системы таково:		1 и	1,	1. Тогда ещё одно

частное решение исходной системы дифференциальных уравнений имеет вид: x3 e2t , y3 e2t , z3 e2t .

Общее решение начальной системы имеет следующий вид:

x	C (cost	sin t)	C	2	sin t	cost	C		e2t	,
	1			2				3	e2t
y	C cost	sin t	C	2	sin t	cost	C		e2t	,
	1			2				3
z	2C cost		2C		sin t		C	e2t ,
	1			2			3

где C1 , C2 и C3 – произвольные постоянные.

Разберём теперь на примере ситуации 3) и 4), т.е. случаи кратных корней. Пример 6. Найти общее решение системы дифференциальных уравнений

dx	5x	2 y	2z,

dt
dt
dy	2x	y	2z,

dt
dt
dz	2x	2 y	z.

dt
dt

Решение. Характеристическое уравнение для системы таково:

	5	k	2	2
	2		1 k	2	0.
	2		2	1 k
Корнями характеристического уравнения				k 3	7k 2 15k	9	0 являются
действительные числа k1 1,		k2	k3	3 .
Найдём частное решение, соответствующее корню k1						1.	Подставляем

k1 1 в систему (11.9), получаем систему для отыскания неизвестных , и

:
4	2	2	0,
2		2	0,
2	2		0.

Одним из решений этой системы будет следующее решение:			1,	1,
1. Частное решение исходной системы имеет вид	x	et , y	et , z	et .
	1	1	1

Найдём частные решения, соответствующие двукратному корню k 3 .

Их нужно искать в следующем виде:
х = (α1 + β1t)e3t,
y = (α2 + β2t)e3t,	(11.12)
z = (α3 + β3t)e3t.

Продифференцировав эти функции, получим, что

	dx		e3t	3
		1
	dt


dy			e3t	3
		2
	dt


	dz		e3t	3
		3
	dt

13 1t e3t ,

23 2t e3t ,

33 3t e3t .

Подставляя функции и их производные в заданную систему и сокращая на общий множитель e3t, получаем следующие равенства:

β1 + 3α1 + 3β1t = 5α1 – 2α2 – 2α3 + (5β1 – 2β2 – 2β3)t, β2 + 3α2 + 3β2t = 2α1 + α2 – 2α3 + (2β1 + β2 – 2β3)t,

β3 + 3α3 + 3β3t = 2α1 – 2α2 + α3 + (2β1 – 2β2 + β3)t.

Левые и правые части этих равенств являются многочленом первой степени относительно переменной t. Приравнивая в обеих частях свободные члены и коэффициенты при t, получим следующую систему из шести линейных алгебраических уравнений с шестью неизвестными α1, β1, α2, β2, α3, β3:

β1 + 3α1 = 5α1 – 2α2 – 2α3,	3β1 = 5β1 – 2β2 – 2β3,
β2 + 3α2 = 2α1 + α2 – 2α3,	3β2 = 2β1 + β2 – 2β3,
β3 + 3α3 = 2α1 – 2α2 + α3,	3β3 = 2β1 – 2β2 + β3.
После преобразований получим систему:
β1 = 2α1 – 2α2 – 2α3,	β1 = β2 + β3,
β2 = 2α1 – 2α2 – 2α3,	β2 = β1 + β3,
β3 = 2α1 – 2α2 – 2α3,	β3 = β1 – β2.

Из трёх уравнений правого столбца этой системы следует, что β1 = β2, β3 = 0. Полагаем β2 = С (С – произвольная постоянная), тогда и β1 = С. После этого первые три уравнения сведутся к следующим двум:

2α1 – 2α2 – 2α3 = С,

2α1 – 2α2 – 2α3 = 0.

Эта система совместна лишь в случае, когда С = 0. В этом случае будет одно уравнение

α1 – α2 – α3 = 0.

<<< < Предыдущая 1 2 3 4 56 / 106 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.20221.85 Mб25556.pdf
#
13.11.20221.86 Mб35557.pdf
#
13.11.20221.86 Mб15558.pdf
#
13.11.20221.86 Mб15559.pdf
#
13.11.20221.87 Mб15560.pdf
#
13.11.20221.87 Mб25561.pdf
#
13.11.20221.88 Mб55562.pdf
#
13.11.20221.88 Mб75563.pdf
#
13.11.20221.89 Mб15564.pdf
#
13.11.20221.89 Mб05565.pdf
#
13.11.20221.89 Mб05566.pdf