
5561
.pdf
С1, то у(0) = С2, а у′(0) = С1. Учитывая заданные начальные условия, получаем, что С2 = 2, С1 = 5. Подставив эти значения в выражение для общего решения,
получим частное решение |
у |
1 |
х |
2 |
5х 2 . |
|
|
3 |
|
||||
|
|
|
|
|
||
Числовые значения постоянных С1 и С2 при начальных условиях (6.5) в случае, если общее решение уравнения имеет явный вид (6.3), находятся из системы уравнений
|
у(х0 , С1, С2 ) |
у00 , |
(6.6) |
|
у (х0 , С1, С2 ) у01. |
||
|
|
||
Пусть дифференциальное уравнение (6.1) или (6.2) рассматривается на |
|||
отрезке [a, b]. Тогда условия |
|
|
|
|
у(a) = d1, y(b) = d2, |
(6.7) |
|
где d1 |
и d2 – заданные числа, называются краевыми для дифференциального |
||
уравнения второго порядка. |
|
|
|
Краевая задача также может иметь единственное решение. В случае |
|||
явного |
общего решения (6.3) постоянные |
С1 и С2 |
найдутся из системы |
уравнений |
|
|
|
|
у(a, C1, C2 ) |
d1, |
(6.8) |
|
y(b, C1, C2 ) d2. |
||
|
|
||
Рассмотрим для уравнения у′′ = 2х на отрезке [0, |
1] краевую задачу со |
||
следующими однородными условиями: у(0) = 0, у(1) = 0. Так как общее решение
имеет вид |
у |
1 |
х |
3 |
С1х С2 |
, то С1 |
и С2 найдутся из системы уравнений |
|
|
3 |
|
||||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
С2 |
|
0, |
|
||
|
|
|
|
|
|
|
|
|
|
1 |
|
С1 С2 |
0. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
3 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда |
|
С1 |
|
|
1 |
, С2 = 0. Решением |
этой |
краевой задачи является функция |
|||||||
|
|
|
|
3 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
у |
1 |
|
х |
3 |
1 |
х . |
|
|
|
|
|
|
|||
|
3 |
|
|
|
3 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Кроме (6.7), имеются и другие виды краевых условий для дифференциальных уравнений второго порядка.
21
7 Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида
y |
py |
qy 0, |
(7.1) |
где p и q – некоторые постоянные. |
|
|
|
Многочлен вида |
|
|
|
k 2 |
pk |
q |
|
называется характеристическим многочленом линейного дифференциального уравнения второго порядка с постоянными коэффициентами. Уравнение
k 2 pk |
q =0 |
(7.2) |
называется характеристическим уравнением уравнения (7.1). |
|
|
Если в уравнении (7.2) коэффициенты |
p и q – действительные числа и |
|
k1, k2 – его различные действительные корни, то функции ek1x ,ek2 x образуют фундаментальную систему решений однородного уравнения (7.1) и его общее решение имеет вид
|
|
y C ek1x |
C ek2 x , |
|
|
|
|
(7.3) |
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
где С1 и С2 – произвольные постоянные. |
|
|
|
|
|
|
|
|||
Пример. Найти общее решение уравнения y |
3y |
2 y 0 . |
|
|
||||||
Решение. |
Характеристическое |
уравнение |
таково: |
k 2 |
3k |
2 |
0 . |
|||
Корнями характеристического уравнения являются числа |
k1 |
|
2 и |
k2 |
1. |
|||||
Фундаментальную систему решений |
образуют |
функции |
e 2 x , e x . Таким |
|||||||
образом, общим решением является функция |
y C1e 2 x |
C2 e x . |
|
|
||||||
Если в уравнении (7.1) коэффициенты |
p и q – действительные числа, а |
|||||||||
уравнение (7.2) |
имеет |
действительный |
корень k |
кратности |
2, |
то |
||||
фундаментальная |
система |
решений |
уравнения |
(7.1) состоит |
из |
функций |
||||
ekx ,
где С1

Пример. Найти общее решение уравнения y |
8y |
16 y |
0 . |
||
Решение. Характеристическое уравнение таково: k 2 |
8k |
16 0 , откуда |
|||
k 4 2 |
0 . Уравнение имеет действительный корень |
k 4 |
кратности 2. |
||
Фундаментальную систему решений образуют функции |
e4 x , xe4 x . Таким |
||||
образом, общим решением будет функция y |
C1e4 x |
C2 x e4 x . |
|
||
Если в уравнении (7.1) коэффициенты |
p и q – действительные числа и |
||||
уравнение (7.2) имеет комплексно – сопряжённые корни |
i |
(β ≠ 0), то |
|||
каждый корень из этой комплексной пары даёт одну и ту же фундаментальную систему решений линейного однородного уравнения (7.1), которая выглядит
следующим |
|
|
образом: |
e x cos |
x, e x sin |
x . |
Общее |
решение |
|||||||||||||
дифференциального уравнения (7.1) имеет вид |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
y |
|
e x (C cos |
x |
C |
2 |
sin |
x) , |
|
|
(7.5) |
||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||
где С1 |
и С2 – произвольные постоянные. |
|
|
|
|
|
|
|
|
||||||||||||
|
Пример. Найти общее решение уравнения y |
2 y |
9 y |
0 . |
|
||||||||||||||||
|
Решение. Корни характеристического уравнения k 2 |
2k |
9 |
0 таковы: |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
k1, 2 |
1 |
|
i 2 |
2 . |
Фундаментальную |
систему решений |
образуют |
функции |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e x cos 2 |
|
2x, e x sin 2 |
2x . |
|
Общим |
решением |
является |
функция |
|||||||||||||
y C e x |
|
|
|
C e x sin 2 |
|
|
|
|
|
|
|
|
|
|
|||||||
cos 2 |
2x |
2x . |
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
23
8 Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейным неоднородным дифференциальным уравнением второго порядка называется уравнение вида
y py qy f x , |
(8.1) |
где f(x) ≠ 0. Будем его рассматривать с постоянными действительными коэффициентами p, q.
Структура общего решения неоднородного уравнения (8.1) имеет вид
|
|
|
|
у |
|
|
~ |
(8.2) |
|
|
|
|
|
||||
|
|
|
|
|
у у , |
|||
|
|
|
|
|
|
|||
где у – |
общее |
решение соответствующего приведённого |
однородного |
|||||
уравнения, |
~ |
какое-нибудь |
частное решение самого |
неоднородного |
||||
а у – |
||||||||
уравнения.
Нахождение общего решения однородного уравнения с постоянными коэффициентами описано в предыдущей теме и связано с корнями характеристического уравнения (7.2).
Рассмотрим способы нахождения частного решения неоднородного
уравнения (8.1) при специальных видах правой части f(x). |
|
Пусть правая часть уравнения (8.1) имеет вид |
|
f(x) = eσx P (x), |
(8.3) |
n |
|
где σ – некоторое действительное число, называемое контрольным числом
правой части уравнения (8.1), а |
|
|
|
|
P (x) = a |
0 |
+ a |
x + … + a xn |
(8.4) |
n |
1 |
n |
|
|
есть многочлен степени n ≥ 0 с действительными коэффициентами. При |
n = 0 |
|||
(8.4) задаёт многочлен нулевой степени Pn(x) = a0 ≠ 0, который не нужно путать с так называемым нулевым многочленом – функцией, являющейся тождественным нулём.
Заметим, что при σ = 0 правая часть уравнения (8.1) будет представлять собой многочлен (8.4).
Пусть правая часть уравнения (8.1) имеет вид (8.3). Тогда а) если контрольное число σ не является корнем характеристического уравнения
соответствующего приведённого однородного уравнения, то частное решение ~
у
необходимо искать в виде |
|
у = еσх Q (x); |
(8.5) |
n |
|
24
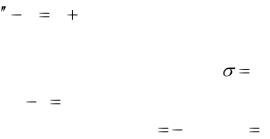
б) если σ является простым (однократным) корнем характеристического
уравнения (7.2), то частное решение находят в виде |
|
у = хеσх Q (x); |
(8.6) |
n |
|
в) если σ является двукратным корнем характеристического уравнения (7.2), то
частное решение надо искать в виде |
|
у = х2еσх Q (x). |
(8.7) |
n |
|
В выражениях (8.5) – (8.7) многочлен Qn(x) |
есть многочлен такой же |
степени, что и многочлен Рn(x), стоящий в правой части (8.3), т.е. он имеет вид
Qn(x) = b0 + b1x + … + bnxn. |
(8.8) |
Коэффициенты br (r = 0, 1, ..., n) многочлена (8.8) подлежат нахождению. Это делается следующим образом. Для соответствующей ситуации функции (8.5), (8.6), (8.7) и входящие в уравнение производные подставляются в (8.1). После этого сокращают на еσх и приравнивают коэффициенты при одинаковых степенях х слева и справа. Получится система алгебраических уравнений для нахождения коэффициентов br многочлена (8.8). Этот способ нахождения чисел br называют методом неопределённых коэффициентов.
Данный вывод о нахождении частных решений уравнения (8.1) относится и к случаю σ = 0, т.е. случаю, когда правая часть f(x) этого уравнения имеет вид (8.4). Тогда в ситуациях б) и в) можно было бы поступить иначе. В ситуации б) имеем q = 0 и можно понизить порядок уравнения, применяя подстановку z = y′. В ситуации в) имеем, что коэффициенты p и q равны нулю; тогда уравнение может быть решено интегрированием, т.к. оно имеет вид у′′ = Pn(x).
Отметим ещё, что ситуации б) и в) приведённого вывода называются
резонансными случаями.
Поясним сформулированный вывод нахождения частных решений рядом
примеров. |
|
|
|
|
|
|
|
|
Пример 1. |
Найти общее решение линейного неоднородного |
|||||||
дифференциального |
уравнения |
второго |
порядка |
с |
постоянными |
|||
коэффициентами |
|
|
|
|
|
|
|
|
|
|
4y |
y |
x |
|
3. |
|
|
Решение. Очевидно, что правая часть |
уравнения представляет собой вид |
|||||||
(8.4), т.е. имеем |
случай, |
когда |
в |
формуле (8.3) |
0 . Корни |
|||
характеристического |
уравнения |
4k 2 |
1 |
0 |
|
соответствующего |
приведённого |
|
однородного дифференциального уравнения таковы: k1 |
0,5 и k2 0,5 . Тогда |
|||||||
25

общее решение приведённого однородного дифференциального уравнения
будет: |
|
y |
C e 0,5x |
C |
2 |
e0,5x , где C |
и C |
2 |
– произвольные постоянные. |
|||||||||||
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
Контрольное |
число |
0 |
не |
|
является |
корнем |
характеристического |
||||||||||||
многочлена, поэтому частное решение |
~ |
|
неоднородного уравнения |
находим в |
||||||||||||||||
y |
|
|||||||||||||||||||
виде |
(8.5): |
y |
b0 |
|
b1x . После |
|
подстановки |
y 0 |
и |
y |
b0 b1x в |
|||||||||
неоднородное уравнение получаем: |
|
b1x b0 |
x |
3. Сравнивая многочлены, |
||||||||||||||||
получим систему для отыскания коэффициентов b0 , |
b1 : |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
b1 |
|
1, |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
b0 |
|
3. |
|
|
|
|
|
||
Тогда b0 |
3 , b1 |
1. Частным решением неоднородного уравнения является |
||||||||||||||||||
|
~ |
x |
3, а общее решение неоднородного уравнения таково: |
|||||||||||||||||
функция y |
||||||||||||||||||||
|
|
|
|
|
|
|
|
y |
C e 0,5x |
|
C |
2 |
e0,5x |
x |
3 . |
|
|
|
||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Найти общее решение линейного неоднородного |
|||||||||||||||||||
дифференциального |
|
|
уравнения |
|
второго |
порядка |
с |
постоянными |
||||||||||||
коэффициентами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
y 25y |
|
x2 |
3x 2 . |
|
|
|
|
||||
|
Решение. |
Правая часть этого |
уравнения |
представляет собой вид (8.4), |
||||||||||||||||
причём многочлен является многочленом второй степени. Корни
характеристического уравнения |
k 2 |
25 |
0 |
соответствующего |
приведённого |
|||||||||||||||||
однородного |
дифференциального |
уравнения |
y |
25y |
0 таковы: |
k1 |
5 и |
|||||||||||||||
k2 |
5 . |
Тогда |
общее |
решение |
однородного |
уравнения |
имеет |
вид |
||||||||||||||
|
|
|
|
5x C |
|
e5x |
|
|
|
|
|
|
|
|||||||||
|
y |
C e |
2 |
, где C |
и C |
2 |
– произвольные постоянные. |
|
|
|
||||||||||||
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Контрольное |
число |
|
|
0 |
не |
является |
корнем |
характеристического |
|||||||||||
многочлена, поэтому частное решение |
~ |
неоднородного уравнения |
находим в |
|||||||||||||||||||
y |
||||||||||||||||||||||
виде |
(8.5): |
|
|
y |
b b x |
b x2 . |
После |
|
подстановки |
y |
2b |
и |
||||||||||
|
|
|
|
|
|
|
|
|
0 |
1 |
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
y |
b |
b x |
b x2 |
|
в неоднородное уравнение получаем равенство: |
|
|
|
|||||||||||||
|
|
|
0 |
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25b x2 |
25b x 2b 25b |
x2 |
3x 2 . |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|
2 |
|
0 |
|
|
|
|
|
|
Система для отыскания коэффициентов b0 , b1 и b2 будет иметь вид
26

|
25b2 |
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
25b1 |
3, |
|
|
|
|
|
|
|
|
|
|
|
|
|
2b2 |
25b0 2. |
|
|
|
|
|
|
|
|
|
|
|
|
Из системы находим b2 |
1 25, |
b1 |
3 25, |
b0 |
52 625. |
Тогда |
частное |
|||||||
|
|
|
|
~ |
52 |
|
3 |
|
|
1 |
|
2 |
|
|
решение неоднородного |
уравнения |
таково: |
y |
|
|
|
|
x |
|
x |
|
. В |
||
625 |
25 |
25 |
|
|||||||||||
результате получаем общее решение неоднородного дифференциального
уравнения y |
|
C e 5 x |
C |
e5 x |
|
52 |
3 |
x |
|
|
|
1 |
x2 . |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
1 |
|
2 |
625 |
25 |
|
25 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Пример |
3. |
Найти общее решение линейного неоднородного |
||||||||||||||||||||||||
дифференциального |
уравнения |
|
второго |
|
|
порядка |
|
с |
постоянными |
||||||||||||||||||
коэффициентами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
9 y |
y 5x3 |
|
7x2 |
|
|
9x 8 |
|
|
|
|
|
|
|
|
|
||||||
при начальных условиях y 0 |
2 , |
y 0 |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Решение. Правая часть уравнения представляет собой вид (8.4) с |
||||||||||||||||||||||||||
многочленом |
третьей |
степени. |
Корнями |
|
характеристического |
уравнения |
|||||||||||||||||||||
9k 2 |
1 0 соответствующего приведённого однородного дифференциального |
||||||||||||||||||||||||||
уравнения 9y |
y |
0 являются числа k1 |
1 3 и k2 |
1 3. Общим решением |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
C e x / 3 |
|
|
ex / 3 , |
|
|
|
|
|
|||||||||||
однородного |
уравнения |
|
будет |
функция |
|
y |
C |
2 |
где |
C |
и C |
2 |
– |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
||
произвольные постоянные. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Контрольное |
число |
0 |
не |
является корнем характеристического |
||||||||||||||||||||||
многочлена, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
находим в |
||||
поэтому частное решение неоднородного уравнения y |
|||||||||||||||||||||||||||
виде |
(8.5): |
y |
b |
b x |
|
b x2 |
b x3 . |
После |
подстановки |
y |
2b |
6b x |
|
и |
|||||||||||||
|
|
|
0 |
1 |
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
3 |
|
|
y b |
b x |
b x2 |
b x |
3 |
в неоднородное уравнение получаем следующее: |
|
|
||||||||||||||||||||
0 |
1 |
|
2 |
3 |
|
|
|
||||||||||||||||||||
|
9 2b 6b x |
|
b b x b x |
2 |
|
b x3 |
5x3 |
7x2 |
9x 8 . |
|
|
|
|||||||||||||||
|
|
|
2 |
3 |
|
0 |
|
1 |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Система для отыскания коэффициентов b0 , b1 , b2 и b3 будет иметь вид
b3 5, b2 7,
54b3 b1 9,
18b2 b0 8,
27

откуда b3 |
5 , b2 |
7 , b1 261, b0 118. Тогда |
частным |
решением |
|||
|
|
~ |
7x |
2 |
5x |
3 |
. |
неоднородного уравнения является функция y 118 261x |
|
|
|||||
Врезультате получаем общее решение неоднородного
дифференциального уравнения |
y C e x / 3 |
C |
ex / 3 |
118 261x 7x2 |
5x3 . |
|
1 |
2 |
|
|
|
Вычислим y 0 и y
и y 0 :
0 :
|
|
|
|
|
|
|
|
|
y 0 C e0 |
|
|
C |
2 |
e0 |
C C |
2 |
, |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
y 0 |
|
1 |
C e0 |
|
|
1 |
C |
|
e0 |
261 |
|
1 |
C |
|
|
1 |
C |
|
261. |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
3 |
1 |
3 |
|
2 |
|
|
|
|
|
|
|
3 |
1 |
|
3 |
2 |
|
|
|
|
|
|||||||||
|
|
|
Сравнивая эти значения с данными начальными условиями примера, |
||||||||||||||||||||||||||||||||||
получим систему для отыскания постоянных C1 |
и C2 : |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
C1 |
C2 |
2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
C |
|
|
|
1 |
C |
|
|
261 |
|
|
1. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
3 |
|
1 |
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
В результате решения системы получаем C1 |
|
341, |
C2 |
|
339. |
Решение |
|||||||||||||||||||||||||||||||
дифференциального |
уравнения |
с |
|
|
начальными |
условиями |
будет |
таково: |
|||||||||||||||||||||||||||||
|
y |
341e x / 3 |
|
339ex / 3 |
118 |
261x |
|
|
7x2 |
|
5x3 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Пример 4. Найти общее решение дифференциального уравнения |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2y |
y |
|
|
|
y |
|
ex |
2x |
|
|
1 . |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Решение. Заметим, что правая часть уравнения представляет собой вид |
||||||||||||||||||||||||||||||||||
(8.3). Контрольное число правой части |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
Найдём общее решение соответствующего приведённого однородного |
||||||||||||||||||||||||||||||||||
дифференциального |
|
уравнения |
|
|
|
2y |
|
y |
|
|
y |
0. |
|
|
|
Корнями |
|
его |
|||||||||||||||||||
характеристического |
уравнения |
2k |
2 |
|
k |
1 |
0 |
|
являются |
числа |
k |
|
1 и |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
k2 |
0,5. |
Тогда общее решение |
|
|
однородного |
|
|
уравнения имеет |
вид |
||||||||||||||||||||||||||||
|
|
|
C e x |
|
|
e0,5x . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
C |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правая часть неоднородного дифференциального уравнения имеет |
вид |
|||||||||||||||||||||||||||||||||
|
f (x) ex |
2x |
|
1 . |
Контрольное |
|
|
число |
|
|
|
|
1 |
|
|
не |
является |
|
корнем |
||||||||||||||||||
характеристического многочлена, поэтому частное решение |
~ |
неоднородного |
|||||||||||||||||||||||||||||||||||
y |
|||||||||||||||||||||||||||||||||||||
уравнения находим в виде (8.5) с многочленом первой степени: |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
ex b |
|
b x . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
28

|
|
Подставляя |
эту |
функцию, |
её |
производные |
|
y |
ex b |
b x |
b |
и |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
|
y |
ex |
b |
b x |
2b |
в |
неоднородное |
уравнение, |
после |
преобразований |
||||||||||||
|
|
|
0 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2b1x 5b1 |
2b0 |
2x 1. |
|
|
|
|
|
|
||||
Система для отыскания коэффициентов b0 |
и b1 |
примет следующий вид: |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2b1 |
2, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5b1 |
2b0 |
1. |
|
|
|
|
|
|
|
|
Тогда |
b1 =1 |
и |
b0 |
3 . Частное решение |
неоднородного |
уравнения есть |
|||||||||||||||
~ |
e |
x |
x |
3 . |
|
|
Общее |
|
решение |
|
представляет |
|
собой |
функцию |
|||||||
y |
|
|
|
|
|
|
|||||||||||||||
y |
C e x |
C |
2 |
e0,5x |
ex |
x |
3 . |
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 5. Указать вид, в котором находится частное решение |
|||||||||||||||||||
дифференциального уравнения |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2y |
|
y y e x x2 |
3x 2 . |
|
|
|
|
|
|
|||
|
|
Решение. Правая часть уравнения представляет собой вид (8.3), при этом |
|||||||||||||||||||
контрольное |
число |
правой |
части |
|
1 |
является |
однократным |
корнем |
|||||||||||||
характеристического многочлена. Поэтому частное решение |
~ |
|
|
|
|||||||||||||||||
y неоднородного |
|||||||||||||||||||||
уравнения находим в виде (8.6): |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
y |
xe x b |
b x |
b x2 . |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
2 |
|
|
|
|
|
|
|
|
|
Пример 6. Указать вид, в котором находится частное решение |
|||||||||||||||||||
дифференциального уравнения |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
y 6 y 9 y e3x x3 |
x2 |
x 1 . |
|
|
|
|
|
||||||
|
|
Решение. Заметим, что правая часть уравнения представляет собой вид |
|||||||||||||||||||
(8.3), причём контрольное число правой части |
|
3. |
|
|
|
|
|
|
|||||||||||||
|
|
Характеристическое |
|
уравнение |
|
k 2 |
6k |
9 |
0 соответствующего |
||||||||||||
приведённого |
|
однородного |
дифференциального |
уравнения |
y |
6y |
9y |
0 |
|||||||||||||
имеет единственный двукратный корень k |
3. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
Поскольку |
контрольное число |
3 |
является |
двукратным |
корнем |
||||||||||||||
характеристического многочлена, то частное решение |
~ |
исходного |
|||||||||||||||||||
y |
|||||||||||||||||||||
неоднородного уравнения находим в виде (8.7): |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
y x |
2e3x b b x b x2 |
b x3 . |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
|
3 |
|
|
|
|
|
|
29

Пусть теперь правая часть уравнения (8.1) имеет специальный следующий
вид: |
|
|
f(x) = eαx [P (x) cos βx + R |
(x) sin βx], |
(8.9) |
n |
m |
|
где α, β – действительные числа, причём β ≠ 0, а Pn(x), Rm(x) – многочлены соответственно степени n ≥ 0 и m ≥ 0 с действительными коэффициентами. При этом не исключается, что в (8.9) могут присутствовать члены только с косинусами или только с синусами; это означает, что один из многочленов может быть нулевым (либо Pn(x) ≡ 0, либо Rm(x) ≡ 0).
Случай β = 0 приводит к изученной ситуации (8.3).
Число σ = α ± βi назовём контрольным числом правой части уравнения
(8.1).
Наибольшую из степеней многочленов, присутствующих в (8.9), обозначим через S:
S = max {n, m}.
Пусть правая часть неоднородного уравнения (8.1) имеет вид (8.9). Тогда а) если контрольное число σ не является корнем характеристического уравнения (7.2) соответствующего приведённого однородного уравнения, то частное
решение находят в виде |
|
|
y = eαx [Q (x) cos βx + L (x) sin βx], |
(8.10) |
|
S |
S |
|
б) если контрольное число σ является корнем характеристического уравнения (7.2) (резонансный случай), то частное решение находят в виде
y = x eαx [Q (x) cos βx + L (x) sin βx]. |
(8.11) |
|
S |
S |
|
В выражениях (8.10) и (8.11) |
многочлены QS(x), LS(x) |
есть многочлены |
высшей степени S каждый со своими коэффициентами br, Cr, подлежащими нахождению методом неопределённых коэффициентов.
К выводу б) сделаем следующее замечание. Комплексные корни алгебраического уравнения (7.2) второй степени с действительными коэффициентами p, q могут являться только сопряжёнными парами α + βi и α – βi, т.е. они у этого уравнения однократны. Поэтому в (8.11) множитель x имеет первую степень (сравните с ситуациями б) и в) предыдущего вывода).
Поясним выводы а) и б) ситуации (8.9) примерами.
Пример 7. Найти общее решение дифференциального уравнения
y |
6 y |
9 y ex x |
1 cos 2x |
sin 2x . |
Решение. Очевидно, что правая часть уравнения представляет собой вид |
||||
(8.9). Контрольное |
число |
правой |
части |
1 не является корнем |
30
