5561

предполагаемое количество населения России через 20 лет, зная, что в 2002 г. оно составляло 145 миллионов человек, а прирост населения составил b 2% .

Решение 1.Установим величины, изменяющиеся в данном явлении: наличное

количество населения y , время t .

2. Выявим законы, связывающие обозначенные величины:

скорость изменения населения прямо пропорциональна наличному

уравнения.

Получили дифференциальное уравнение первого порядка с

7. Определяем параметры С и К

Так как общее решение

у = Сеkt,

то постоянная С определяется из начального условия у(0) = у0. Получим уравнение у0 = Сеk∙0 для нахождения С. Следовательно, С = у0 и решение, удовлетворяющее начальному условию, имеет вид у = у0 еk∙t. Теперь надо найти параметр К. Для этого воспользуемся условием задачи: через год население

41

Частное решение у = у0 еk∙t при t = 1 принимает значение у0 еk. Тогда для нахождения параметра К имеем следующее уравнение:

откуда ek 1 100b . Следовательно, равенство

задаёт численность населения в момент времени t при начальном количестве у0 и годовом приросте b%.

Первое начальное условие y 0 y0 . Найдём второе начальное условие из условия задачи. Поскольку через год население увеличилось на b %, то годовой

прирост в процентах от y0 составит 100b y0 , а количество населения через год

становится равным y0 + 100b y0 . Таким образом, второе начальное условие имеет

b

вид y 1 y0 + 100 y0 .

8. Исследуем полученное решение

Построим график частного решения (рисунок 2).

42

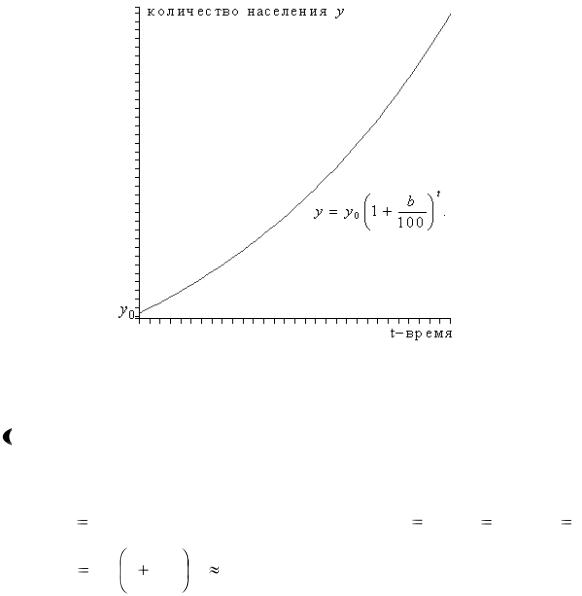
Рисунок 2 – график частного решения

Из графика видно, что с увеличением времени t количество населения y t увеличивается.

Найдём предполагаемое количество населения России через 20 лет, зная, что в 2002 г. оно составляло 145 миллионов человек, а прирост населения

43

(10.2) при любой точке x0 из соответствующего множества и любых конкретно выбранных числах y01, ..., y0n .

Одним из основных методов нахождения решения однородных нормальных систем является метод исключения неизвестных. С помощью этого метода данная система сводится к одному уравнению n – го порядка относительно одной неизвестной функции.

Пример. Найти общее решение системы уравнений

второго уравнения системы и заменяя функцию z её выражением из первого, приходим к линейному однородному уравнению второго порядка относительно одной неизвестной функции:

Найдём частное решение данной системы, удовлетворяющее начальным условиям

надо выделить такие числа С1, С2 , чтобы выполнялись эти начальные условия.

Рассмотрим ещё один метод нахождения общего решения однородной системы линейных дифференциальных уравнений первого порядка в нормальной форме.

Пусть при каждом l 1,..., n система функций

является частным решением однородной системы линейных уравнений. Назовём систему решений (10.3) фундаментальной системой решений однородной системы, если определитель

называется определителем Вронского, а матрица W(x) – фундаментальной матрицей системы.

Каждый набор функций (10.3) можно трактовать как n – мерный вектор

46

Yl xy1 l x , ... , yn l x,

соответствующими координатами которого являются функции (10.3). В случае фундаментальной системы решений это означает, что векторы Yl x( l 1,..., n )

линейно независимы на интервале a,b .

Если (10.3) есть фундаментальная система решений однородной системы в нормальной форме, то общее решение этой системы имеет вид

где c1,..., cn – произвольные постоянные. Запишем (10.5) в развёрнутом виде:

11 Системы линейных однородных дифференциальных уравнений с постоянными коэффициентами

Ограничимся подробно изучением таких систем, состоящих из двух и трёх уравнений. Для изучения систем с большим числом уравнений надо обратиться к дополнительной литературе.

Рассмотрим систему двух уравнений с двумя неизвестными функциями x t , y t независимой переменной t

вкоторой все коэффициенты asj ( s, j 1, 2 ) являются постоянными

действительными числами.

Фундаментальную систему решений системы (11.1) будем искать в виде

47

с постоянными коэффициентами , и k , которые надо найти. Не исключается, что эти постоянные могут быть комплексными числами.

Перенося все члены в одну часть равенства и группируя коэффициенты при

,, получим

Система (11.3) есть однородная система из двух линейных алгебраических уравнений с двумя неизвестными , . Из алгебры известно, что однородная система линейных алгебраических уравнений имеет нетривиальное (ненулевое) решение тогда и только тогда, когда определитель этой системы равен нулю. Таким образом, неизвестный параметр k в (11.2) должен быть корнем уравнения

уравнения (11.5) есть действительные числа, то его комплексные корни входят сопряжёнными парами a bi .

Действительные корни характеристического уравнения (11.4), т.е. алгебраического уравнения (11.5), называются собственными числами (собственными значениями) матрицы

Аa11 a12 a21 a22

48

системы дифференциальных уравнений (11.1), а соответствующие этим числам нетривиальные решения ( , ) системы (11.3) – собственными векторами матрицы А.

Пусть корни k1, k2 вещественны (действительны) и различны (k1 k2); иначе говоря, матрица А имеет простой спектр. Подставляя эти корни по очереди в систему (11.3), найдём соответствующие какие-нибудь конкретные собственные векторы ( 1, 1 ) и ( 2 , 2 ) . Напомним, что собственные векторы,

отвечающие простому корню, определяются с точностью до постоянной величины. По формулам (11.2) найдутся четыре функции, являющиеся фундаментальной системой решений системы (11.1). Пары этих функций x1,y1 и x2,y2 будут частными решениями системы (11.1), т.к. решения искались в виде (11.2) путём подбора , и k . Эти два решения будут линейно независимы.

Это, во-первых, следует из того, что определитель, составленный из функций, образующих фундаментальную систему решений, будет отличен от нуля (предоставляется читателю проверить это). С другой стороны, линейная независимость этих двух решений следует из алгебраического факта: система собственных векторов ( 1, 1 ) , ( 2 , 2 ) простого спектра линейно независима.

Общее решение системы (11.1) в случае вещественных различных корней k1, k2 будет иметь вид

где C1,C2 – произвольные постоянные.

Пример 1. Найти общее решение системы дифференциальных уравнений

Решение. Эта система является системой вида (11.1) с матрицей системы

Характеристическое уравнение (11.4) для данной системы таково:

49

частное решение системы задаётся функциями x2(t)= e4t , y2(t)= 3e4t . Найденные два решения являются линейно независимыми, т.к.

Следовательно, функции х1(t) = e-t, x2(t) = e4t, y1(t) = – 2e-t, y2 = 3e4t образуют фундаментальную систему решений. Тогда согласно (11.6) общее решение данной системы имеет вид

произвольные постоянные коэффициенты.

Пусть корни уравнения (11.4) являются комплексными. Выше отмечено, что для уравнений (11.5) с действительными коэффициентами они являются сопряжённой парой k1,2= a bi . При этом каждый такой корень даст одну и ту же фундаментальную систему решений.

Подставив корень k1=a+bi в систему (11.3), найдём соответствующий вектор , . По этому вектору из (11.2) найдётся фундаментальная система решений:

50