
- •Введение
- •1 Основные понятия
- •2 Арифметический, геометрический и гармонический ряды
- •3 Необходимый признак сходимости ряда
- •4 Основные свойства сходящихся рядов
- •5 Упражнения и вопросы для самопроверки
- •6 Положительные ряды
- •7 Упражнения и вопросы для самопроверки
- •8 Знакопеременные ряды
- •9 Упражнения и вопросы для самопроверки
- •Библиографический список
- •Алфавитно-предметный указатель

24. Докажите равенства lim |
n! |
0 , lim |
5n |
0 , lim |
n3 |
0 . |
|
nn |
n! |
4n |
|||||
n |
n |
n |
|
25.Для каких рядов можно применять признак Маклорена – Коши?
26.Какого типа интегралы используются в интегральном признаке?
27.Укажите те , при которых обобщённый гармонический ряд сходится, и те , при которых он расходится.
8 Знакопеременные ряды
Определение 6. Числовой ряд, содержащий бесконечное количество как положительных, так и отрицательных членов, расположенных в совершенно произвольном порядке, называется знакопеременным.
Частным случаем знакопеременных рядов являются знакочередующиеся ряды, к изучению которых сначала и приступим.
Определение 7. Знакочередующимся называется ряд, любые два соседних члена которого являются числами противоположных знаков.
Последнее определение означает, что любой знакочередующийся ряд может быть записан в одном из следующих видов:
u |
u |
2 |
u |
3 |
u |
4 |
1 n 1u |
n |
1 n |
|
1u |
n |
, |
(40) |
|||
1 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
u |
u |
2 |
u |
3 |
1 n u |
n |
|
1 n u |
n |
, |
|
|
(41) |
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
где все un 0 .
Для таких рядов Лейбницем был установлен очень простой достаточный признак их сходимости. Сформулируем и докажем его для ряда (40).
Теорема 9 (признак Лейбница). Если члены знакочередующегося ряда (40) монотонно убывают по абсолютной величине ( un 1 un для всех n ) и стремятся к нулю ( un 0 при n 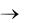 ), то ряд сходится.
), то ряд сходится.
51

Доказательство. Согласно определению 3 нужно доказать, что
lim Sn |
S . |
Это равенство будет доказано, |
если его установим как при |
|||||
n |
|
|
|
|
|
|
|
|
чётном n |
n |
2m , так и при нечётном n n |
2m 1 ; при этом m |
1,2,3,.... |
||||
Рассмотрим сначала чётную частичную сумму, т.е. сумму |
n 2m |
|||||||
первых членов ряда (40). Очевидно, что её можно записать в виде |
|
|||||||
|
|
S2m |
u1 |
u2 |
u3 |
u4 |
u2m 1 u2m . |
|
Из условия теоремы |
u1 |
u2 |
u3 |
следует, что все выражения в скоб- |
||||
ках этой суммы положительны. Следовательно, сама эта сумма положительна S2m 0 . С возрастанием номера m эта сумма увеличится, т.к. добавится ещё одно положительное слагаемое. Теперь эту сумму запишем так:
S2m u1  u2 u3
u2 u3 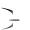 u4 u5
u4 u5 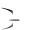
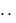
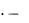 u2m 2 u2m 1
u2m 2 u2m 1 u2m .
u2m .
В этой записи все выражения в скобках положительны и u2m 0 . Таким
образом, S2m получается вычитанием из u1 |
0 некоторого количества по- |
||
ложительных чисел. Следовательно, |
S2m u1 |
при любом m |
1,2,3,.... |
Таким образом, установлено, |
что последовательность |
S2m чётных |
|
частичных сумм ряда возрастает и ограничена сверху. По признаку существования предела монотонной последовательности она имеет конечный предел, который обозначим S :
|
|
|
|
|
|
lim |
S2m |
S . |
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
Проверим теперь, что и частичные сумы с нечётными номерами схо- |
|||||||||
дятся к тому же числу S . Очевидно, что для таких сумм справедливо ра- |
||||||||||
венство |
S2m 1 S2m |
u2m . |
Перейдём в этом равенстве к пределу, когда |
|||||||
m |
. |
Так |
как по |
условию |
теоремы lim u2m |
0 , |
то получим |
|||
|
|
|
|
|
|
|
|
m |
|
|
следующее: |
|
|
|
|
|
|
|
|
||
|
|
|
lim S2m 1 |
|
lim S |
2m |
lim u2m S 0 |
S . |
|
|
|
|
|
m |
|
m |
|
m |
|
|
|
|
Объединяя результаты |
lim |
S2m |
S, lim S2m 1 |
S |
, можно запи- |
||||
|
|
|
|
|
|
m |
|
m |
|
|
сать |
lim Sn |
S , т.е. ряд сходится. Теорема доказана. |
|
|
||||||
|
n |
|
|
|
|
|
|
|
|
|
52

Ряд (41) получается из ряда (40) умножением его на 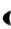 1 . Тогда при
1 . Тогда при
выполнении условий теоремы 9 u1 u2 u3 |
; lim un 0 этот ряд |
|
n |
также сходится.
Знакочередующиеся ряды (40) и (41) при выполнении двух условий
признака Лейбница ( un 1 |
un |
для всех n , lim un 0 ) называют рядами |
|
|
n |
лейбницевского типа. Как только что было установлено, любой ряд лейбницевского типа сходится.
Пример 31. Очевидно, что ряд |
|
1 n |
1 |
1 |
1 |
|
1 |
1 |
1 |
яв- |
||
|
|
|
|
|
|
|
|
|
|
|||
n 1 |
n |
|
2 |
|
3 |
4 |
5 |
|||||
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ляется рядом лейбницевского типа и, следовательно, сходится. Знакочере-
|
|
1 n |
|
дующийся ряд |
|
|
также будет сходящимся. |
|
|
||
n |
1 |
n |
|
|
|
||
Замечание 15. Ни одно из условий признака Лейбница нельзя отбро-
сить. Если lim un 0 , то общие члены рядов (40) и (41) не будут стре-
n
миться к нулю. Будет нарушено необходимое условие сходимости числового ряда (см. пункт 3); такой ряд будет расходиться. Нельзя отбросить и условие монотонности ( un 1 un для всех n ). Действительно, рассмотрим знакочередующийся ряд
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
10 |
|
2 |
102 |
3 |
103 |
|
n |
10n |
||||||||
|
|
|
|
|||||||||||||
Последовательность |
un |
из абсолютных величин этого ряда не является |
||||||||||||||
монотонной (отметим, что un |
|
0 ). Этот ряд будет расходящимся (дока- |
||||||||||||||
зать самостоятельно). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Замечание 16. |
Рассмотрим ряд (40). При доказательстве теоремы |
|||||||||||||||
было установлено, что последовательность S2m чётных частичных сумм,
возрастая, приближается к сумме S этого ряда. Последовательность S2m 1 нечётных частичных сумм, убывая, будет сходиться к S . Действительно,
S1 u1, S3 u1  u2 u3 , S5 u1
u2 u3 , S5 u1  u2 u3
u2 u3 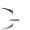 u4 u5 , … и так как каж-
u4 u5 , … и так как каж-
53
дая из разностей в скобках положительна, |
то S1 S3 S5 |
. Таким об- |
разом, если ряд (40) является рядом Лейбница, то |
|
|
S2m S S2m 1 m |
1,2,... . |
(42) |
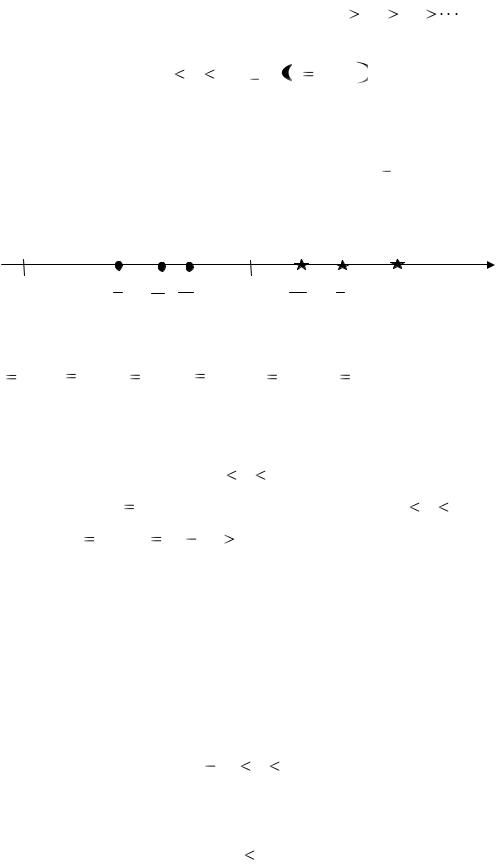
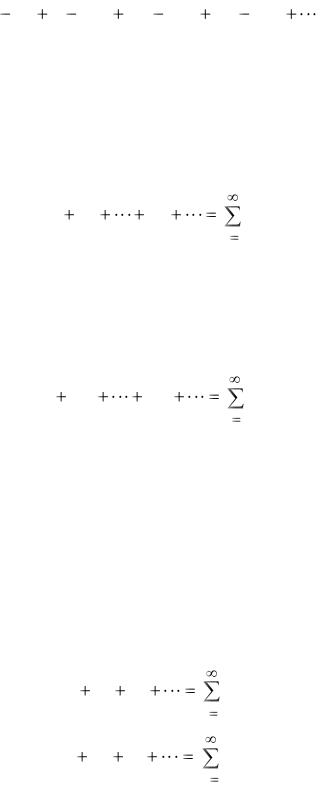
Неравенства (42) означают следующее: если ряд (40) есть ряд лейбницевского типа, то чётные частичные суммы S2m являются приближениями к сумме S ряда с недостатком, а нечётные суммы S2m 1 – с избытком. Это свойство проиллюстрировано ниже на рисунке для первого ряда из примера 31.
|
S2 |
S4 S6 |
S |
S5 |
S3 |
S1 |
|
|
|
||||||
0 |
1 |
7 |
37 |
|
47 |
5 |
1 |
2 |
12 |
60 |
|
60 |
6 |
||
|
|
|
|||||
На рисунке изображены только шесть первых частичных сумм этого ряда;
при S |
1, S |
|
1 |
, S |
|
|
5 |
, S |
|
7 |
, S |
|
|
47 |
, S |
|
37 |
. |
|
|
2 |
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
|||||||
1 |
|
2 |
|
6 |
|
12 |
|
60 |
|
60 |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Замечание 17. Сумма ряда (40), удовлетворяющего условиям при- |
||||||||||||||||||||
знака Лейбница, положительна и меньше его первого члена, т.е. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
0 |
S |
|
u1 . |
|
|
|
(43) |
|||
Докажем это. При m |
1 неравенство (42) имеет вид S2 |
S S1. Остаётся |
||||||||||||||||||
заметить, что S1 |
|
u1, |
S2 u1 |
u2 |
0 . |
|
|
|
|
|
|
|
||||||||
Замечание 18. Можно доказать, что чётные частичные суммы ряда |
||||||||||||||||||||
(41) лейбницевского типа приближаются к его сумме S |
убывая, а нечёт- |
|||||||||||||||||||
ные – возрастая. Доказательство этого факта рекомендуем провести читателю, а геометрическую иллюстрацию сделать для второго ряда из примера 31 (см. замечание 16).
Замечание 19. Если ряд (41) лейбницевского типа, то его сумма от-
рицательна и больше первого члена (сравните с замечанием 17), т.е. |
|
|||
u1 |
S 0 . |
(44) |
||
Замечание 20. Таким образом, для любого ряда лейбницевского типа |
||||
(40) или (41) имеет место неравенство |
|
|
||
|
S |
|
u1, |
(45) |
|
|
|||
где u1 – модуль первого члена соответствующего ряда (см. определение 7). Неравенство (45) следует из неравенств (43) и (44).
54

Всё сказанное можно выразить иначе: сумма любого ряда лейбницевского типа имеет тот же знак, что и первый член ряда, а по абсолютной величине меньше его модуля.
Это свойство таких рядов позволяет достаточно просто вычислять приближённо их суммы с помощью приближения частичными суммами (напомним, что сумма ряда есть предел частичной суммы). Значение S будет найдено таким образом тем точнее, чем больше номер частичной суммы Sn . При этом с помощью неравенства (45) можно дать и оценку точности (погрешности) такого приближённого вычисления. Поясним сказанное более подробно.
В силу равенства (17) абсолютная величина получаемой при этом погрешности S Sn 
 равна rn , где rn – сумма остатка ряда после n -го члена. Остаток же ряда лейбницевского типа имеет один из следующих видов:
равна rn , где rn – сумма остатка ряда после n -го члена. Остаток же ряда лейбницевского типа имеет один из следующих видов:
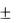 un 1 un 2
un 1 un 2 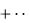
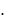 ,
,
т.е. является знакочередующимся рядом Лейбница вида (40) или (41). Знак первого члена остатка зависит от того, будет номер n чётным или нечётным. В случае ряда (40) при чётном n знак остатка будет положительным, а при нечётном – отрицательным (для ряда (41) – наоборот). Так как к остатку применимо замечание 20, то для суммы остатка имеет место неравенство
rn |
|
un 1 |
un 1. |
(46) |
Последнее неравенство позволяет оценить ошибку приближённого равенства S Sn .
Сказанное можно сформулировать так: ошибка, совершаемая при замене суммы S ряда Лейбница некоторой его частичной суммой Sn , имеет тот же знак, что и первый отброшенный член, а по абсолютной величине меньше его модуля (знак поправки вычисления совпадает со знаком этого члена).
Замечания 16 и 18 позволяют выяснить, будет ли при этом сумма вычислена с избытком или с недостатком.
55

Пример 32. Рассмотрим первый из примера 31 сходящийся знакочередующийся ряд лейбницевского типа. Его n -я частичная сумма
|
Sn |
|
1 |
1 |
|
1 |
1 |
1 |
|
1 |
1 |
n |
1 1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
3 |
4 |
5 |
6 |
|
|
n |
||||||||
|
|
|
|
|
|
|
|
|||||||||||
отличается от суммы |
S этого ряда (согласно (43) |
0 |
|
S 1) на величину |
||||||||||||||
меньшую, чем |
1 |
|
. Это значит, что ряд сходится довольно медленно (для |
|||||||||||||||
|
|
|||||||||||||||||
n 1 |
||||||||||||||||||
малой погрешности при отбрасывании остатка ряда номер n должен быть большим). Возьмём теперь конкретные чётные и нечётные номера n .
Пусть n |
4, |
тогда S |
S4 |
1 |
|
1 |
|
1 |
1 |
7 |
; при этом сумма вычислена с |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
2 |
|
3 |
4 |
12 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
недостатком, а ошибка вычисления положительна и меньше |
1 |
|
0,2 (оста- |
|||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|||
ток |
ряда |
начинается |
|
|
с |
положительного |
|
члена |
1 |
). |
Если |
n 5 , то |
||||||||||||||||||||||||||||||||||
5 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
S |
S5 1 |
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
|
47 |
; теперь сумма ряда вычислена с избытком, а |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
2 |
|
|
|
3 |
|
|
4 |
|
|
|
5 |
|
|
60 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ошибка вычисления отрицательна и меньше |
|
1 |
, т.к. остаток ряда начинает- |
|||||||||||||||||||||||||||||||||||||||||||
6 |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ся с отрицательного члена |
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример 33. Теперь рассмотрим второй из примера 31 лейбницев- |
|||||||||||||||||||||||||||||||||||||||||||||
ский ряд. Сумма n первых членов этого ряда |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Sn |
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
1 n |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
3 |
|
4 |
|
5 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
будет согласно (44) удовлетворять неравенствам 1 |
S |
0 и отличаться от |
||||||||||||||||||||||||||||||||||||||||||||
суммы S этого ряда снова на величину меньшую, чем |
|
|
1 |
. Проведём вы- |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
n |
1 |
|||||||||||||||||||||||||||||||||||||||||||||
числения для конкретных чётных и нечётных номеров n . При n |
5 имеем |
|||||||||||||||||||||||||||||||||||||||||||||
S |
S5 |
1 |
|
|
1 |
|
|
1 |
1 |
|
1 |
|
|
47 |
; при этом сумма ряда вычислена с недо- |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
2 |
|
|
3 |
4 |
|
5 |
|
60 |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
статком, ошибка вычисления положительна и меньше |
1 |
, т.к. остаток ряда |
||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|||||
56

начинается |
с |
положительного |
члена |
|
|
|
1 |
. Пусть |
n |
6 , |
тогда |
|||||||||||||
|
|
6 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
S S6 |
1 |
1 |
|
1 |
1 |
1 |
|
1 |
47 |
1 |
|
37 |
; теперь сумма ряда вычис- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2 |
|
3 |
4 |
5 |
6 |
60 |
6 |
|
60 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
лена с избытком, ошибка вычисления отрицательна и меньше |
1 |
|
(остаток |
|||||||||||||||||||||
7 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ряда начинается с отрицательного члена |
1 |
|
). |
|
|
|
|
|||||||||||||||||
7 |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Часто задают точность , с которой нужно приближённо вычислить сумму ряда лейбницевского типа. Тогда нужно найти, сколько должно быть членов ряда в его частичной сумме Sn . В силу (46) это число нахо-
дится из неравенства un 1 |
. |
|
|
|
|
|
Пример 34. Указать, сколько членов ряда |
|
|
1 n |
1 |
нужно оста- |
|
n 1 |
n ! |
|
||||
|
|
|
|
|||
|
|
|
|
|
||
вить в частичной сумме, чтобы сумма ряда была вычислена с точностью до 0,01. Очевидно, что этот ряд сходится, т.к. является рядом лейбницевского
типа; при этом |
un 1 |
1 |
|
. По условию примера |
0,01; |
следователь- |
||||||
|
|
|||||||||||
|
|
|||||||||||
|
|
|
n 1 ! |
|
|
|
|
|
|
|||
но, номер n определяется из неравенства |
1 |
|
0,01. Выпишем все зна- |
|||||||||
|
|
|||||||||||
n 1 ! |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
чения числа |
n |
1 !, пока |
не получим число больше 100: |
2! |
1 2 2 , |
|||||||
3! 1 2 3 6 , |
4! |
1 2 3 4 |
24 , 5! 1 2 3 4 5 |
|
120 . |
Тогда |
n |
4 и для |
||||
вычисления суммы ряда с точностью до 0,01 достаточно ограничиться суммой первых четырёх его членов, т.е. вычислить S4 . Решение примера завершено. Отметим ещё следующее: погрешность при этом будет поло-
жительной, |
т.к. первый отброшенный член |
|
u5 |
1 |
|
1 |
|
положителен; |
|||||||||||
|
|
|
|
|
|
||||||||||||||
5! |
120 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
S4 |
1 |
1 |
|
1 |
|
1 |
|
5 |
даст приближённое значение суммы ряда с недо- |
||||||||||
2 |
|
6 |
24 |
8 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
статком (см. замечание 16), не превышающим |
|
1 |
. |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
120 |
|
|
|
|
|
|
|||
57
Не следует думать, что сходятся только знакочередующиеся ряды лейбницевского типа. Примером сходящегося знакочередующегося ряда, не являющегося рядом Лейбница, является ряд
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
2 |
102 |
22 |
103 |
23 |
104 |
||||||||
(его сходимость будет установлена в дальнейшем, см. пример 36).
До сих пор изучался частный случай знакопеременного ряда – знакочередующийся ряд. Перейдём теперь к изучению произвольных знакопеременных рядов.
Пусть
u1 u2 |
un |
un |
(47) |
|
n |
1 |
|
есть произвольный знакопеременный ряд (см. определение 6). В отличие от рассмотренных знакочередующихся рядов символом un снова обозначается n -й член ряда, а не его абсолютная величина. Одновременно с рядом (47) рассмотрим положительный ряд
u1 |
|
u2 |
|
un |
|
|
un |
, |
(48) |
|
|
|
|
|
n |
1 |
|
|
|
составленный из модулей членов ряда (47).
Теорема 10 (теорема Коши). Из сходимости ряда (48) следует сходимость ряда (47).
Доказательство. Рассмотрим в отдельности положительные члены ряда (47) и абсолютные величины его отрицательных членов, при этом для них введём обозначения bk и cm . Перенумеруем bk и cm в том порядке, в котором они встречаются в ряде (47). Теперь составим два положительных
ряда |
|
|
|
|
b1 |
b2 |
b3 |
bk , |
(49) |
|
|
k |
1 |
|
c1 |
c2 |
c3 |
cm . |
(50) |
|
|
m 1 |
|
|
58

Через Sn и Sn обозначим, соответственно, частичные суммы рядов (47) и
(48). Через Bk и Cm обозначим те частичные суммы рядов (49) и (50), ин-
дексы |
которых |
удовлетворяют |
неравенствам |
k n , |
m n (при этом |
|
n k |
m ). Тогда очевидны равенства |
|
|
|
||
|
|
Sn |
Bk |
Cm , |
|
(51) |
|
|
Sn |
Bk |
Cm . |
|
(52) |
По условию теоремы ряд (48) сходится. Тогда существует конечный |
||||||
предел |
lim Sn |
S . Из (52) следует, что Bk |
S и Cm |
S . При этом по- |
||
|
n |
|
|
|
|
|
ложительные суммы Bk и Cm |
монотонно возрастают. Следовательно, су- |
|
ществуют конечные пределы |
lim Bk |
B , lim Cm C , т.е. ряды (49) и |
|
k |
m |
(50) сходятся (отметим, что S 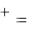
Перейдём теперь к пределу в равенстве (51). Только что было установлено существование конечных пределов величин, стоящих справа. Сле-
довательно, существует конечный предел lim Sn |
S . При этом |
n |
|
S B C . |
(53) |
Теорема доказана. |
|
Эта теорема даёт возможность судить о сходимости некоторых знакопеременных рядов. В этих случаях вопрос о сходимости знакопеременного ряда сведётся к исследованию соответствующего положительного ряда. Для положительных рядов имеется ряд признаков их сходимости, изу-
ченных в пункте 6. |
|
|
|
|
|
|
|
|
Пример 35. Рассмотрим ряд |
cos x |
|
cos 2x |
|
cos3x |
|
cos nx |
, |
1 |
22 |
32 |
|
n2 |
||||
|
|
|
||||||
где x – любое число. Наряду с этим рядом рассмотрим следующий ряд из
модулей его членов: |
|
cos x |
|
cos 2x |
|
|
cos 3x |
|
|
cos nx |
|
. Согласно |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
22 |
|
|
32 |
|
|
n2 |
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
теореме 3 этот последний положительный ряд будет сходиться, т.к. |
||||||||||||||||
|
|
|
|
|
|
cos nx |
|
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
n2 |
|
|
|
|
|
|||
59
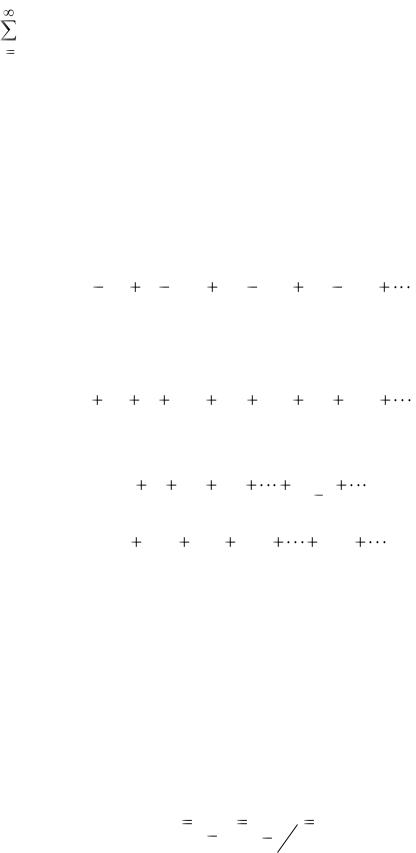
и ряд |
1 |
сходится (см. примеры 18 и 28). По теореме 10 будет сходить- |
|
|
n2 |
||
n |
|
|
|
1 |
|
||
ся и исходный ряд.
При доказательстве теоремы 10 было установлено полезное утверждение (53): при условии сходимости ряда (48) сумма знакопеременного ряда (47) равна разности между суммой ряда (49), составленного из одних положительных членов данного ряда, и суммой ряда (50), составленного из абсолютных величин отрицательных членов ряда (47).
Пример 36. Исследуем упоминавшийся ранее ряд
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
, |
(54) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10 |
2 |
102 |
22 |
103 |
23 |
104 |
||||||||||
который не является рядом Лейбница. Из модулей его членов составим положительный ряд
1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
1 |
, |
(55) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
10 |
2 |
102 |
22 |
103 |
23 |
104 |
|||||||||||
|
|
|
|||||||||||||||
который можно рассматривать как сумму двух следующих рядов:
1 |
1 |
|
|
1 |
|
1 |
|
|
|
1 |
|
|
, |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
22 |
|
23 |
|
|
|
2n 1 |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
1 |
|
1 |
1 |
|
1 |
. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
102 |
|
103 |
104 |
|
10n |
|||||||||||
|
|
|
|
|||||||||||||||
Это утверждение основано на переместительном свойстве сходящихся рядов (читателю рекомендуем обратиться к дополнительной литературе, т.к. в данном пособии это свойство положительных рядов не изучалось). Свойство означает, что в положительных сходящихся рядах можно менять местами члены и это не влияет ни на сходимость ряда, ни на величину его суммы. Последние два ряда являются геометрическими (см. пункт 2). Оба ряда сходятся, а их суммы вычисляются по формуле (11). Для первого ряда:
B |
a |
|
|
1 |
|
2 |
, |
|
|
|
|
|
|
||||
1 q |
1 |
1 |
2 |
|||||
|
|
|
||||||
|
|
|
|
|
|
|
||
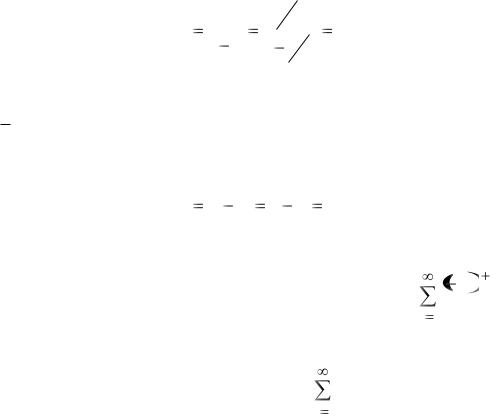
для второго ряда:
60
|
a |
1 |
1 |
|
||||
C |
10 |
. |
||||||
|
|
|
|
|
||||
1 q 1 |
1 |
|
9 |
|||||
|
|
|
|
10 |
|
|
|
|
Тогда на основании свойства 3 ряд (55) сходится (при этом его сумма рав-
на 2 19 ). Согласно теореме 10 будет сходиться и ряд (54). Из равенства (53)
находится его сумма:
S B C 2 |
1 |
1 |
8 |
. |
|
|
|
|
|
9 |
9 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
Обратная теорема к теореме 10 не имеет места. Из сходимости ряда |
|||||||||
(47) не следует, что сходится и ряд (48). Например, ряд |
|
|
1 n |
1 |
по при- |
||||
n 1 |
n |
|
|||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||
знаку Лейбница сходится (см. пример 31), в то время как ряд из модулей
его членов является гармоническим рядом |
|
1 |
, который, как установлено |
|
1n |
||||
n |
|
|||
ранее, расходится (см. пункт 2 и пример 28).
Таким образом, признак Коши есть достаточный признак сходимости знакопеременного ряда, но не необходимый. Это значит, что существуют такие знакопеременные ряды, которые сходятся, а ряды, составленные из модулей их членов, расходятся. Только что и был приведён пример такого ряда. В связи с этим для знакопеременных рядов вводятся понятия условной и абсолютной сходимости.
Определение 8. Если сходится не только данный знакопеременный ряд (47), но и ряд (48) из модулей членов исходного ряда, то ряд (47) называется абсолютно сходящимся. Если же сам ряд (47) сходится, а ряд (48) расходится, то знакопеременный ряд (47) называется условно или неабсо-
лютно сходящимся рядом.
Замечание 21. С помощью понятия абсолютной сходимости теорему 10 (признак Коши) можно сформулировать следующим образом: всякий абсолютно сходящийся знакопеременный ряд есть ряд сходящийся.
Абсолютно сходящимися рядами являются знакопеременные ряды из примеров 35 и 36.
61

|
Пример 37. Ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
|
|
1 |
|
|
|
|
1 n 1 |
|
(56) |
|||||
|
2 |
3 |
|
|
4 |
|
|
|
|
|
n |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
будет |
абсолютно сходящимся |
|
при |
1 |
и |
условно сходящимся при |
||||||||||||||
0 |
1. Действительно, |
ряд |
1 |
1 |
1 |
|
1 |
1 |
, составлен- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
2 |
|
3 |
|
4 |
|
|
|
n |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
ный из модулей членов исходного ряда (56), представляет собой обобщен-
ный гармонический ряд (13), который сходится при |
1 и расходится при |
||||
0 |
1 (см. пункт 3, примеры 16 и 28). Сам же знакочередующийся ряд |
||||
(56) при |
1 сходится по признаку Лейбница. Заметим, что при |
0 ряд |
|||
(56) расходится, т.к. при таких |
его члены не стремятся к нулю (не вы- |
||||
полнено необходимое условие сходимости ряда). |
|
|
|||
|
Замечание 22. Пусть для знакопеременного ряда (47) соответствую- |
||||
щий ряд (48) строго положителен ( un 0 для всех n ). Для таких знакопе-
ременных рядов справедлив аналог предельного признака Даламбера. Именно: пусть существует конечный предел
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
un 1 |
|
|
D ; |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
un |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||||
тогда при D |
|
1 ряд (47) абсолютно сходится, а при D |
1 расходится. До- |
||||||||||||||||||||
кажем это. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
Применим |
предельный |
признак |
|
Даламбера к ряду (48). Так как |
||||||||||||||
|
|
un 1 |
|
u |
n 1 |
|
, то |
D lim |
|
un |
1 |
|
lim |
|
u |
n 1 |
|
. Если D |
1, то ряд (48) схо- |
||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
un |
|
|
un |
|
|
|
un |
|
|
|
|
un |
||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
||||||||
дится, а это и значит, что ряд (47) сходится абсолютно.
Пусть теперь D 1. Тогда ряд (48) расходится, но из его расходимости нельзя сделать никакого вывода о поведении исходного ряда (47). Однако его расходимость в этом случае можно доказать непосредственно без
привлечения ряда (48). Действительно, |
поскольку lim |
un |
1 |
|
D 1, то |
|||||||||||||
un |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
для |
|
достаточно больших номеров n |
будет выполняться |
|
неравенство |
|||||||||||||
|
|
un |
1 |
|
1 или |
|
un 1 |
|
un |
|
. Последнее неравенство означает, что при боль- |
|||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
un |
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
62
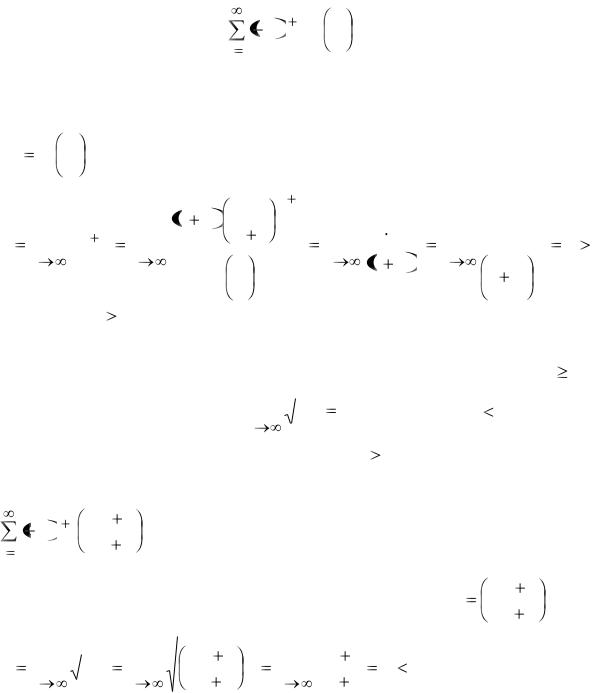
ших n абсолютные величины членов ряда (47) будут возрастать и, следовательно, члены ряда не будут стремиться к нулю. Ряд расходится в связи с тем, что не выполнено необходимое условие его сходимости.
Пример 38. Исследуем знакочередующийся ряд
1 n 1n ! |
5 |
n . |
|
n |
|||
n 1 |
|
||
|
|
Так как непосредственная проверка условий теоремы Лейбница является
затруднительной, |
то |
воспользуемся замечанием |
22. |
Очевидно, |
что |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
5 |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
un |
|
n ! |
|
|
|
|
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
5 |
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
un 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 nn |
|
|
|
5 |
|
|
|
|
|
5 |
|
||||||||||||||||
|
D |
lim |
|
|
|
lim |
n 1 |
|
|
|
|
|
|
|
lim |
|
|
lim |
|
|
|
|
|
1. |
||||||||||||||||||||||||||||||
|
|
|
|
un |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n 1 n |
|
|
|
|
|
n |
|
|
e |
|||||||||||||||||||||
|
|
|
n |
|
|
|
|
n |
n ! |
5 |
|
|
|
|
|
|
|
|
n |
|
|
|
n |
|
1 |
1 |
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Поскольку D |
1, то ряд расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
Замечание 23. Аналогично общему признаку Даламбера из замеча- |
|||||||||||||||||||||||||||||||||||||||||||||||||||
ния 22 применяется и общий радикальный признак Коши. Пусть |
|
un |
|
0 и |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
существует конечный предел |
lim n |
|
u |
n |
|
K . Тогда при |
K 1 знакопере- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
менный ряд (47) абсолютно сходится, а при K |
|
1 он расходится. |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Пример |
39. Исследуем |
|
на |
сходимость |
знакочередующийся |
ряд |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
n 1 |
|
|
|
|
2n |
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Чтобы не проверять выполнение условий теоремы |
|||||||||||||||||||||||||||||||||||||
n 1 |
|
|
|
|
|
|
|
|
4n |
3 |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
|
1 |
|
n |
|
|
||
Лейбница, |
|
|
|
|
|
применим |
замечание |
23. |
|
Так |
|
как |
|
un |
|
|
, |
|
то |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
4n |
|
3 |
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim n |
2n |
1 |
|
n |
|
lim |
2n |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
K |
lim n |
|
u |
n |
|
|
|
|
1. Данный ряд сходит- |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
4n |
3 |
|
|
4n |
3 |
|
2 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ся, причём абсолютно.
В заключение приведём без доказательства некоторые свойства знакопеременных рядов.
63
