
- •Введение
- •1 Основные понятия
- •2 Арифметический, геометрический и гармонический ряды
- •3 Необходимый признак сходимости ряда
- •4 Основные свойства сходящихся рядов
- •5 Упражнения и вопросы для самопроверки
- •6 Положительные ряды
- •7 Упражнения и вопросы для самопроверки
- •8 Знакопеременные ряды
- •9 Упражнения и вопросы для самопроверки
- •Библиографический список
- •Алфавитно-предметный указатель

Предположим противное, т.е. что гармонический ряд сходится. Тогда
lim Sn |
lim S2n S . Переходя |
к |
пределу в последнем неравенстве, |
|||
n |
n |
|
|
|
|
|
получим, что |
|
|
|
|
|
|
|
S S |
1 |
|
или 0 |
1 |
. |
|
2 |
|
2 |
|||
|
|
|
|
|
||
Получили противоречие. Следовательно, предположение о сходимости гармонического ряда неверно, т.е. гармонический ряд расходится.
Ряд вида
1 |
1 |
1 |
1 |
1 |
, |
(13) |
|||
|
|
|
|
|
|
|
|||
n 1 n |
2 |
3 |
|
n |
|||||
|
|
|
|
||||||
где 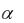 – любое вещественное число, называется обобщённым гармониче-
– любое вещественное число, называется обобщённым гармониче-
ским рядом. Он сходится при |
1, расходится при |
1. Это будет |
установлено в дальнейшем. При |
1 ряд (13) является гармоническим и, |
|
следовательно, расходится. |
|
|
3 Необходимый признак сходимости ряда
Выясним, есть ли что-нибудь общее у сходящихся рядов, заданных своим общим членом. Оказывается, что общий член сходящегося ряда с возрастанием номера n стремится к нулю.
Теорема 1. Если ряд (6) сходится, то
|
|
lim un |
0 . |
(14) |
|
|
|
n |
|
|
|
Доказательство. Так как ряд (6) по условию теоремы сходится, то |
|||||
lim Sn |
S . Очевидно, что |
lim Sn 1 |
S |
( Sn 1 пробегает ту же последо- |
|
n |
n |
|
|
|
|
вательность чисел, что и Sn ). |
Так как |
|
|
|
|
|
Sn u1 |
un 1 |
un |
Sn 1 |
un , |
то при n |
1 имеем равенство |
|
|
|
|
|
|
un Sn |
Sn 1 . |
|
|
Переходя в этом равенстве к пределу, получим |
|
||||
14

lim un |
lim Sn |
lim Sn 1 S S 0 , |
n |
n |
n |
что и требовалось доказать.
Обратная теорема к теореме 1, вообще говоря, неверна. Условие (14) есть лишь необходимое условие сходимости ряда, но не является достаточным. Из того, что выполняется (14), не следует, что ряд сходится. При выполнении условия (14) ряд может как сходиться, так и расходиться.
Примером |
расходящегося ряда, для которого выполнено условие (14), |
||||
является |
рассмотренный в предыдущем пункте гармонический ряд |
||||
(12) (очевидно, что lim un |
lim |
1 |
0 ). |
||
n |
|||||
|
n |
n |
|
||
У сходящихся рядов, рассмотренных ранее, необходимое условие их сходимости было выполнено.
С другой стороны, если условие (14) не выполнено ( lim un 0 или
n
этот предел не существует), то ряд расходится.
К расходящимся рядам относятся, например, ряды со следующими
общими членами: un |
|
n , un |
n2 , un |
|
|
|
|
|
|
, un |
|
|
|
|
n |
1 |
, |
|
|
|
1)n 1. |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
un ( |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||||
При |
0 обобщённый гармонический ряд (13) расходится, так как |
|||||||||||||||||||||||||||||||||||||||||||||||||||
при любых таких |
его общий член un |
|
|
1 |
|
не стремится к нулю. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Рассмотрим |
обобщённый гармонический |
|
|
ряд |
(13) |
при |
|
1 |
, |
|||||||||||||||||||||||||||||||||||||||||||
2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
т.е. ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
n |
1 |
|
|
|
n |
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Необходимое условие (14) выполнено, т.к. |
|
lim |
1 |
|
|
0 |
. Для его n -й |
ча- |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||||||||
стичной суммы, начиная со второй, выполняется неравенство |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Sn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n , |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
2 |
|
|
3 |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
15

из которого следует, что Sn увеличивается до бесконечности вместе с увеличением номера n . Согласно определению 3 данный ряд расходится, хотя необходимое условие сходимости выполнено.
|
По аналогии с этим простым случаем |
1 |
докажем, что ряд (13) |
|||||||||||||
|
|
|||||||||||||||
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
расходится при всех |
, удовлетворяющих двойному неравенству 0 |
1. |
||||||||||||||
Отметим, что для таких |
необходимое условие (14) выполнено. |
|
||||||||||||||
|
Так как все члены частичной суммы |
|
|
|
||||||||||||
|
|
|
Sn |
1 |
|
1 |
|
1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2n |
|
n |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
этого ряда не меньше чем |
1 |
|
и она состоит из n членов, то |
|
||||||||||||
n |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
Sn |
n |
1 |
n1 . |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
n |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Перейдём к пределу в этом неравенстве |
с учётом того, что |
при |
|||||||||||||
0 |
1 число 1 |
0. Получим следующее: |
|
|
|
|||||||||||
|
|
lim Sn |
|
|
lim n1 |
. |
|
|
||||||||
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|||
Следовательно, lim Sn |
; ряд (13) при таких |
|
расходится. |
|
||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 Основные свойства сходящихся рядов
Понятие суммы ряда (бесконечного числа слагаемых) существенно отличается от понятия суммы конечного числа слагаемых, так как основано ещё и на предельном переходе. Сумма ряда (число S ) не есть сумма всех его членов, а есть предел его частичных сумм. Однако некоторые свойства конечных сумм переносятся и на бесконечные суммы (ряды), но чаще всего лишь при выполнении определённых условий. В некоторых же случаях известные свойства конечных сумм нарушаются. В связи с этим рассмотрим в данном пункте некоторые свойства рядов.
16

Свойство 1. Сходящийся ряд не может иметь две различные суммы (сумма S сходящегося ряда единственна).
Это следует из того, что последовательность Sn частичных сумм сходящегося ряда имеет пределом единственное число S (теорема о единственности предела сходящейся последовательности).
Свойство 1 напоминает нам свойство конечной суммы: сумма конечного числа слагаемых единственна.
Свойство 2. Если ряд |
un |
u1 u2 |
un |
сходится и его |
|
|
n |
1 |
|
|
|
сумма равна S, то ряд |
сun |
сu1 |
сu2 |
сun |
, где с – произволь- |
n |
1 |
|
|
|
|
ное число, также сходится и его сумма равна c  S .
S .
Доказательство. Пусть Sn есть частичная сумма ряда |
|
un , а Sn* – |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
частичная сумма ряда |
cun . Из свойств конечных сумм следует равен- |
||||||||||||
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
ство сu |
сu |
сu |
c u |
u |
2 |
u |
n |
, т.е. S* |
c |
S |
n |
. |
Так как по- |
1 |
2 |
n |
1 |
|
|
n |
|
|
|
|
|||
стоянный множитель можно вынести за знак предела, то |
|
|
|
|
|||||||||
|
|
|
lim Sn* |
|
c |
lim S n |
c S. |
|
|
|
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
Последнее означает (см. определение 3), что ряд |
cun |
сходится и его |
|||||||||||
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
сумма есть число c S . |
|
|
|
|
|
|
|
|
|
|
|
||
Замечание |
1. Перепишем |
|
утверждение этого свойства в виде |
||||||||||
cun c |
un . Таким образом, на сходящиеся ряды переносится правило |
||||||||||||
n 1 |
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
вынесения постоянного общего множителя c за скобку, как в конечных суммах.
17

Свойство 3. Если ряды |
un и |
vn |
сходятся, а их суммы равны S1 |
n |
1 |
n 1 |
|
и S2 соответственно, то сходятся и ряды |
(un vn ) , полученные путём |
||
|
|
n |
1 |
почленного сложения (вычитания) соответствующих членов исходных ря-
дов, причём сумма каждого будет равна, соответственно, S1 |
|
S2 . |
|
|||
|
Доказательство. Обозначим n -е |
частичные суммы |
рядов |
un , |
||
|
|
|
|
|
n |
1 |
vn |
и |
(un vn ) через Sn(1) , Sn(2) , |
Sn соответственно. |
На основании |
||
n 1 |
n |
1 |
|
|
|
|
свойств конечных сумм получается очевидное равенство Sn |
S (1) |
S (2) . |
||||
Пользуясь теоремами о пределах (предельным переходом в равенствах и пределом суммы), получаем
lim S |
n |
lim S (1) |
S (2) |
lim S (1) |
lim S (2) |
S |
S |
2 |
. |
||||
n |
n |
n |
n |
n |
n |
n |
n |
1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
Таким образом, каждый из рядов |
(un |
|
vn ) |
|
сходится, |
а сумма равна |
|||||||
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
S1 S2 соответственно.
Свойство 3 означает, что сходящиеся ряды можно почленно складывать и вычитать так же, как это делается с конечными суммами.
Легко доказать, что сумма (разность) сходящегося и расходящегося рядов является расходящимся рядом. Заметим, что с почленным сложением расходящихся рядов надо соблюдать осторожность. Сумма (разность) двух расходящихся рядов может быть как сходящимся, так и расходящим-
ся рядом. Поясним это примерами. |
|
||
Пример 10. Ряды |
n и |
n2 |
расходятся, т.к. их общие члены не |
n |
1 |
n 1 |
|
стремятся к нулю. Очевидно, что ряд |
n n2 , составленный путём сум- |
||
|
|
|
n 1 |
мирования членов исходных рядов, также расходится.
18
|
|
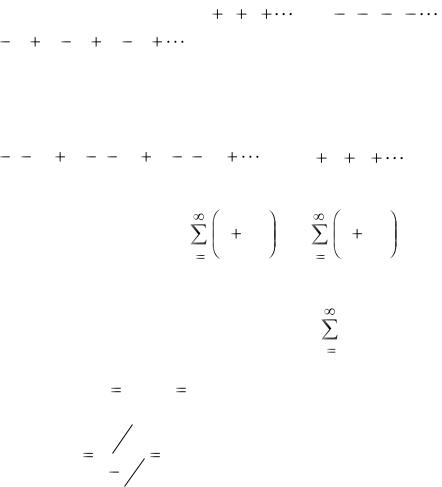
Пример 11. Ряды 1 1 |
1 |
|
|
и |
|
1 |
1 |
1 |
расходятся. |
Ряд |
||||||
(1 |
1) |
(1 |
1) |
(1 1) |
|
, полученный почленным суммированием соот- |
||||||||||||
ветственных членов этих рядов, сходится; его сумма равна нулю. |
|
|||||||||||||||||
|
|
Пример 12. Рассмотрим ряды предыдущего примера. Почленно вы- |
||||||||||||||||
читая |
из |
|
членов |
первого |
ряда |
|
члены |
|
второго, |
получим |
ряд |
|||||||
(1 |
( |
1)) |
(1 |
( 1)) |
(1 |
( 1)) |
или |
2 |
2 |
2 |
, который расходится |
|||||||
так же, как и образующие его ряды. |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Пример 13. Ряды |
|
1 |
2 |
|
и |
|
|
1 |
1 |
расходятся, т.к. их об- |
||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
n 1 |
3n |
n |
1 |
|
3n |
|||||||||||
щие члены не стремятся к нулю. Вычитая из членов первого ряда соответ-
ствующие члены второго, получим ряд |
1 |
, являющийся геометриче- |
|||||||||||||||
|
|
||||||||||||||||
n 1 3n |
|||||||||||||||||
ским рядом с a |
|
1 |
|
и |
q |
1 |
|
. Из пункта 2 следует, что он сходится, причём |
|||||||||
3 |
3 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
его сумма S |
|
|
13 |
|
|
|
|
1 |
. |
|
|
|
|
|
|
||
1 |
1 |
|
|
|
|
2 |
|
|
|
|
|
|
|||||
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
Как известно, для конечных сумм справедливо сочетательное свой-
ство (ассоциативность сложения). Теперь установим, что и любой схо-
дящийся ряд обладает этим свойством.
Свойство 4. Если в сходящемся ряде произвольно сгруппировать члены ряда, не меняя при этом порядка их расположения, то полученный таким образом ряд будет сходиться и иметь ту же сумму, что и исходный ряд.
Доказательство. После произвольного объединения членов исходного ряда в группы каждая такая группа (несколько слагаемых, заключённых в скобки) будет отдельным членом нового ряда. Каждая частичная сумма этого нового ряда будет представлять собой какую-то частичную сумму исходного ряда (номер частичной суммы нового ряда не будет больше номера частичной суммы исходного ряда). Таким образом, последовательность частичных сумм преобразованного ряда будет представлять собой подпоследовательность последовательности частичных сумм исход-
19

ного ряда. Из теории пределов известно, что всякая подпоследовательность сходящей последовательности имеет тот же предел, что и сама последовательность. Следовательно, свойство доказано.
Полной аналогии с обычными конечными суммами ряды не имеют. Опускать скобки (если они есть) в членах сходящихся рядов, не нарушая сходимости ряда, нельзя. Так, например, ряд
(1 1) (1 1) (1 1) 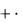
 ,
,
сумма которого равна нулю, обращается после опускания скобок в расходящийся ряд
1 1 1 1 
(см. пример 7, а также пункт 3). С другой стороны, после группировки членов расходящегося ряда может получиться сходящийся ряд. Например, группируя члены расходящегося ряда
1 1 1 1 |
1 n 1 |
по два, получим ряд
(1 1) (1 1) (1 1) 
из нулей, который сходится.
Рассмотрим ещё несколько свойств сходящихся рядов.
Определение 4. Ряд, который получается из ряда (6) путём отбрасывания у него некоторого числа первых по порядку членов, называется остатком этого ряда. Остаток
uk un 1 un 2 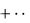
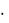 un k
un k 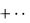
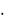 (15) k n 1
(15) k n 1
называется n-м остатком или остатком ряда (6) после n-го члена.
Свойство 5. Если сходится ряд (6), то сходится любой из его остатков; обратно, из сходимости любого остатка (15) вытекает сходимость исходного ряда.
Доказательство. 1. Пусть ряд (6) сходится и имеет сумму S . Докажем, что остаток (15) при любом n сходится. Частичную сумму первых n m членов рядов (6) можно записать в виде
Sn m (a1 |
an ) (an 1 |
an m ) Sn (an 1 |
an m ) , |
20

где Sm* an 1 |
an |
m есть m -я частичная сумма ряда (14). Следова- |
|||||||
тельно, справедливо равенство |
|
|
|
|
|
|
|
||
|
|
Sm* |
Sn |
m |
Sn . |
|
|
|
(16) |
Так как ряд (6) сходится, что lim Sn |
m |
S ; слагаемое Sn |
в (16) с увели- |
||||||
|
|
m |
|
|
|
|
|
|
|
чением m не меняется |
lim Sn |
Sn |
. Тогда |
Sm* при m |
имеет ко- |
||||
|
|
m |
|
|
|
|
|
|
|
нечный предел, который обозначим |
r |
r |
lim S* |
. Таким образом, |
|||||
|
|
|
|
n |
n |
m |
m |
|
|
|
|
|
|
|
|
|
|
|
|
ряд (15) сходится. Кроме того, после перехода в формуле (16) к пределу
при m |
получим для суммы rn |
остатка равенство |
|
|
|
|
|
rn |
S |
Sn . |
|
|
(17) |
2. Теперь пусть известно, что сходится остаток (15). Докажем, что |
||||||
сходится и исходный ряд (6). Зафиксируем в равенстве |
|
|
|
|||
|
Sn m |
Sn |
Sm* |
|
|
(18) |
( Sn m |
и Sn – соответствующие частичные суммы исходного ряда (6)) |
|||||
номер n и перейдём к пределу при m |
. Так как ряд (15) сходится, то |
|||||
lim S* существует (этот предел обозначен r ). Величина |
S |
n |
при фикси- |
|||
m |
m |
|
n |
|
|
|
|
|
|
|
|
|
|
рованном номере n остаётся постоянной. Следовательно, существует предел величины Sn m при m  ; ряд (6) сходится. При этом для его суммы верно равенство
; ряд (6) сходится. При этом для его суммы верно равенство
S Sn rn , |
(19) |
получающееся из (18) путём предельного перехода. Заметим, что последнее равенство равносильно полученному ранее равенству (17). Свойство доказано.
Замечание 2. Равенство (19) означает, что сумма всякого сходящегося ряда может быть получена сложением какой-либо частичной суммы этого ряда и суммы соответствующего остатка.
Замечание 3. Из равенства (18) следует, что если ряд расходится, то расходится его остаток и, наоборот, если расходится остаток, то расходится и ряд.
21
