
- •Введение
- •1 Основные понятия
- •2 Арифметический, геометрический и гармонический ряды
- •3 Необходимый признак сходимости ряда
- •4 Основные свойства сходящихся рядов
- •5 Упражнения и вопросы для самопроверки
- •6 Положительные ряды
- •7 Упражнения и вопросы для самопроверки
- •8 Знакопеременные ряды
- •9 Упражнения и вопросы для самопроверки
- •Библиографический список
- •Алфавитно-предметный указатель

6 Положительные ряды
Определение 5. Числовой ряд, все члены которого неотрицательны,
т.е. для любого n N выполняется неравенство |
|
un 0 , |
(21) |
называют положительным рядом . |
|
Такие ряды точнее было бы называть рядами с неотрицательными членами. В данном параграфе будем заниматься установлением сходимости или расходимости подобных рядов. Их изучение облегчит и изучение рядов любого знака. В частности, ряды с неположительными членами ( un 0 ) путём умножения на 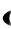 1
1 переходят в ряды с неотрицательными членами и, следовательно, можно будет сделать выводы и об их сходимости.
переходят в ряды с неотрицательными членами и, следовательно, можно будет сделать выводы и об их сходимости.
Сейчас будет приведён критерий (необходимый и достаточный при-
знак) сходимости положительных рядов. Он основан на определении 3 и
свойствах сходящихся последовательностей.
Теорема 2. Для того чтобы положительный ряд сходился, необходимо и достаточно, чтобы его частичные суммы Sn были ограничены сверху.
Доказательство. 1. Необходимость признака. Если ряд сходится, то
существует конечный предел S lim Sn (см. определение 3). Всякая же
n
сходящаяся последовательность Sn ограничена (это есть теорема из теории пределов последовательностей). Необходимость установлена. Заметим, что ограниченность снизу частичных сумм Sn очевидна; в силу (21)
имеем, что Sn 0 .
2. Достаточность признака. Дано, что частичные суммы положитель-
ного ряда ограничены сверху: |
Sn |
M для всех n N . Далее, из условия |
(21) имеем, что |
|
|
Sn 1 |
Sn |
an 1 Sn , |
т.е. последовательность Sn частичных сумм положительного ряда есть неубывающая последовательность. В теории монотонных последовательностей имеется утверждение: всякая неубывающая ограниченная сверху по-
28

следовательность сходится, т.е. существует конечный предел последовательности Sn . Согласно определению 3 ряд является сходящимся. Достаточность установлена.
Замечание 5. Так как всякая сходящаяся последовательность ограничена, то у всякого сходящегося ряда (6) последовательность Sn его частичных сумм (в силу определения 3) будет ограниченной. Это условие, также являющееся необходимым условием сходимости любого ряда, не является достаточным (оно достаточно только для положительных рядов).
Например, частичные суммы ряда 1 1 1 |
1 |
ограничены 0 Sn 1 , |
||||
однако он не является сходящимся. |
|
|
|
|||
Замечание 6. Если последовательность Sn частичных сумм положи- |
||||||
тельного |
ряда |
сверху не |
ограничена, |
то |
ряд будет |
расходящимся |
un |
. |
Это следует |
из того, что |
неубывающая |
неограниченная |
|
n 1 |
|
|
|
|
|
|
сверху последовательность стремится к |
. |
|
|
|||
Замечание 6 и теорема 2 приводят к выводу: положительный ряд всегда имеет сумму; эта сумма будет конечной, если частичные суммы ряда ограничены сверху, и бесконечной S 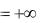
 в противном случае.
в противном случае.
Приведённый критерий мало удобен при исследовании на сходимость конкретных положительных рядов, так как трудно устанавливать ограниченность сверху последовательности частичных сумм. Однако он будет применён в дальнейших теоретических рассуждениях. На его основе будут выведены некоторые достаточные условия (признаки) сходимости. К ним, прежде всего, относятся так называемые признаки сравнения.
Теорема 3. Пусть даны два положительных ряда |
|
|||||
|
un |
u1 |
u2 |
un |
, |
(22) |
n |
1 |
|
|
|
|
|
|
vn |
v1 |
v2 |
vn |
, |
(23) |
n |
1 |
|
|
|
|
|
причём для всех n N выполняется неравенство |
|
|
||||
|
|
|
un |
vn . |
|
(24) |
29

Тогда из сходимости ряда (23) следует сходимость ряда (22) (то есть, если сходится ряд с большими членами, то сходится и ряд с меньшими членами); из расходимости ряда (22) следует расходимость ряда (23) (то есть, если расходится ряд с меньшими членами, то ряд с большими членами также расходится).
Доказательство. Обозначим частичные суммы рядов (22) и (23), со-
ответственно, через Sn(1) и Sn(2) . Из определения 2 n -й частичной суммы ряда и неравенства (24) следует неравенство
Sn(1) Sn(2) .
Пусть ряд (23) сходится; тогда по теореме 2 его частичные суммы ограни-
чены сверху: Sn(2) M (необходимое условие). В силу предыдущего нера-
венства получим, что и Sn(1) M , откуда снова по теореме 2 (достаточное условие) следует сходимость ряда (22).
Вторая часть утверждения этой теоремы есть следствие первой. В самом деле, если бы ряд (23) сходился, то согласно первому утверждению сходился бы и ряд (22), что противоречит предположению о его расходи-
мости. Это же утверждение вытекает и из неравенства Sn(1) Sn(2) (более детальное рассуждение предоставляем читателю).
Замечание 7. Так как отбрасывание конечного числа членов ряда не влияет на его сходимость (см. свойство 5 и замечание 4), то утверждение теоремы 3 остаётся верным при условии, что неравенство (24) выполнено не для всех номеров n , а лишь начиная с некоторого номера N .
При решении конкретных примеров с помощью теоремы 3 надо проводить сравнение с рядами, о сходимости (расходимости) которых уже известно. Например, можно сравнивать исследуемый ряд с гармоническим рядом (12) или с каким-нибудь положительным геометрическим рядом
(10).
1
Пример 14. Исследуем на сходимость ряд n 1 2 3n .
30
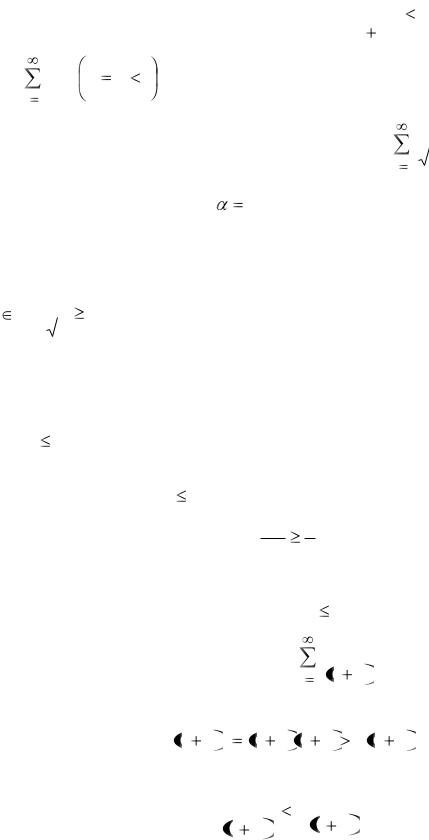
Так как для всех n справедливо неравенство |
|
1 |
|
|
1 |
|
|
и геометрический |
||||||||||
|
3n |
|
|
3n |
||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
ряд |
1 |
q |
1 |
|
1 сходится, то по теореме 3 сходится и данный ряд. |
|||||||||||||
|
|
|
|
|||||||||||||||
n 1 3n |
3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Пример 15. Исследуем на сходимость ряд |
|
|
1 |
|
|
, т.е. обобщённый |
|||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
n |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
гармонический ряд (13) с |
1 |
(его расходимость уже установлена в |
||||||||||||||||
2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
пункте 3 на основании определения 3). Сравним его с гармоническим рядом (12), расходимость которого установлена в пункте 2. Так как при всех
n N |
1 |
1 |
(члены исследуемого ряда не меньше членов гармоническо- |
|||
|
|
|
|
n |
||
|
n |
|
|
|||
|
|
|
|
|
||
го ряда) и гармонический ряд расходится, то по теореме 3 расходится и данный ряд.
Пример 16. Исследуем ещё раз обобщённый гармонический ряд (13) при 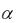 1 с помощью данного признака сравнения (при таких
1 с помощью данного признака сравнения (при таких 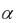 этот ряд уже изучен в пункте 3).
этот ряд уже изучен в пункте 3).
Поскольку при 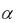 1 для любого номера n справедливо неравенство
1 для любого номера n справедливо неравенство
1 1 n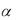 n
n
и так как гармонический ряд расходится, то теорема 3 позволяет утверждать расходимость ряда (13) для всех 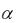 1.
1.
Пример 17. Докажем, что ряд |
|
|
|
1 |
|
сходится. При любом n |
||||
|
|
|
|
|
|
|||||
n |
1 n |
1 2 |
|
|||||||
имеет место неравенство |
|
|
|
|
|
|
|
|
|
|
n 1 2 |
n 1 n |
1 |
|
n n |
1 |
|||||
и, следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
n |
1 2 |
|
n n |
1 |
|
|
|||
31

Так как ряд с большими членами |
1 |
|
сходится (см. пример 5), то со- |
||||
|
|
||||||
n n |
1 |
||||||
|
|
|
|
|
|||
гласно теореме 3 данный ряд тоже сходится. |
|||||||
Пример 18. Ряд |
1 |
отличается от ряда примера 17 только пер- |
|||||
|
|
||||||
1 n2 |
|||||||
n |
|
|
|
|
|||
вым членом, равным единице, и поэтому сходится. Данный ряд есть част-
ный случай обобщённого гармонического ряда |
2 . |
Иногда более удобно применять другой признак, который можно назвать предельным признаком сравнения.
Теорема 4. Пусть ряд (22) – положительный, а ряд (23) строго поло-
жительный vn |
0 . Если существует конечный, |
отличный от нуля, предел |
||||||||||||||
отношения общих членов этих рядов |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
lim |
|
un |
K |
K |
0 , |
|
|
|
(25) |
||
|
|
|
|
|
|
vn |
|
|
|
|||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
||
то оба ряда сходятся или расходятся одновременно. |
|
|
|
|||||||||||||
Доказательство. Если предел (25) существует, то по определению |
||||||||||||||||
предела числовой последовательности для любого числа |
0 |
найдётся |
||||||||||||||
номер N такой, что для всех n |
|
N будет выполняться неравенство |
||||||||||||||
|
|
un |
|
K |
|
|
или K |
|
|
un |
|
K |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
vn |
|
|
|
|
|
vn |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как по условию теоремы vn |
0 , то для всех n |
N будет выполняться |
||||||||||||||
неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K |
vn |
un |
K |
|
|
vn . |
|
|
(26) |
|||
Поскольку un |
0, vn |
|
0 и предположено, что K |
0 , то K |
0 . В силу про- |
|||||||||||
извольности числа |
его можно выбрать таким, чтобы число K |
было |
||||||||||||||
положительным |
K |
|
|
0 ; для этого |
|
0, может быть, придётся взять |
||||||||||
сколь угодно малым. Неравенства (26) позволяют применять теорему 3 (первый признак сравнения). Именно, будем сравнивать положительные ряды с членами K 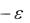 vn , un , K
vn , un , K 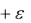 vn .
vn .
32

Пусть ряд с членами un сходится. Так как K |
vn |
un , то по пер- |
||
вому признаку сравнения (теорема 3) ряд с членами |
K |
vn сходится, а |
||
тогда по свойству 2 сходится и ряд с членами vn . |
|
|
|
|
Пусть теперь сходится ряд с членами vn . Тогда по свойству 2 схо- |
||||
дится ряд с членами K |
vn . Но так как согласно (26) un |
K |
vn , то |
|
по теореме 3 сходится и ряд с членами un . |
|
|
|
|
Итак, сходимость одного из рядов (22) и (23) при vn |
0 влечёт за со- |
|||
бой сходимость другого ряда (тем самым, если один из них расходится, то расходится и другой). Теорема доказана.
Пример 19. Исследуем с помощью этого признака ряд из примера 17. Сравним его со строго положительным рядом примера 5, который схо-
дится. |
Так |
как K |
lim |
1 |
n |
|
1 2 |
|
|
lim |
|
n n 1 |
|
lim |
|
|
n |
1, то ряд |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
1 n n 1 |
|
|
|
n 1 2 |
|
|
n 1 |
|||||||||||||||||||||||
|
|
|
|
|
n |
|
n |
|
|
|
|
n |
|
|
|
||||||||||||||||
|
|
1 |
|
сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 n |
1 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Пример 20. Исследуем ряд |
|
|
|
|
|
1 |
|
|
|
. Сравним его также с рядом |
||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
n |
11 |
|
n2 |
|
||||||||||||||||||||||||||
примера 5. |
Так как |
K |
lim |
1 1 |
|
|
n2 |
|
|
lim |
n n |
1 |
|
1 |
, то данный ряд |
||||||||||||||||
1 n n |
1 |
|
|
|
|
n2 |
|||||||||||||||||||||||||
|
|
|
|
|
|
n |
|
|
n |
|
|
1 |
|
|
|
|
|
|
|||||||||||||
сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример 21. Исследуем сходимость ряда |
|
2n |
|
5 |
, сравнив его с |
|||||||||||||||||||||||||
|
|
|
n2 |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
||
расходящимся гармоническим рядом. Так как |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
K |
lim |
2n |
|
5 |
|
n2 |
|
|
lim |
|
2n |
5 n |
|
2 , |
|
|
|||||||||||
|
|
|
|
|
|
1 n |
|
|
|
|
|
|
|
n2 |
|
|
|
||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||||||
то данный ряд, как и гармонический, расходится.
Пример 22. Исследуем на сходимость ряд |
ln 1 |
1 |
. Отметим, |
|
n |
||||
n |
1 |
|
||
|
|
что необходимое условие (14) его сходимости выполняется:
33

|
|
|
|
lim un |
|
lim ln 1 |
1 |
ln1 0 . |
|
||
|
|
|
|
|
|
|
|||||
|
|
|
n |
|
|||||||
|
|
|
|
n |
n |
|
|
|
|||
Сравним |
его с |
гармоническим |
рядом, |
используя теорему |
4. Так как |
||||||
|
ln 1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
n |
|
|
|
||
|
n |
|
|
|
1 , то исследуемый |
ряд, как и |
|||||
|
|
|
|
|
|||||||
K lim |
|
|
|
lim ln 1 |
|
|
|
lne |
|||
1 n |
|
|
|
n |
|||||||
n |
|
|
n |
|
|
|
|
|
|||
гармонический, расходится.
К рассмотренным признакам сравнения близки часто используемые признаки Даламбера и Коши в непредельной и предельной формах. Они основаны на сравнении рассматриваемого положительного ряда со сходящимся геометрическим рядом
|
|
|
|
|
|
|
aqn |
aq |
aq2 |
|
|
|
aqn |
0 q 1 |
|||
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
или с расходящимся рядом |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
Теорема 5 (признак Даламбера). Пусть ряд (22) строго положи- |
||||||||||||||
тельный |
un 0 . |
Если для всех n или начиная с некоторого номера N |
|||||||||||||||
выполняется условие |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
un |
1 |
|
|
q 1, |
(27) |
|
|
|
|
|
|
|
|
|
|
|
|
un |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
то ряд сходится; если же |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
un 1 |
|
1, |
(28) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
un |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
то ряд расходится. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Доказательство. |
Неравенство |
(27) |
равносильно неравенству |
|||||||||||
u |
n |
1 |
qu |
n |
или |
u |
n 1 |
u qn |
. Хотя последнее неравенство может быть вы- |
||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
полнено только начиная с некоторого номера N , на основании замечания 7 |
|||||||||||||||||
к теореме 3 ряд |
|
un |
un |
0 будет сходиться, так как сходится геометри- |
|||||||||||||
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
ческий ряд с членами u qn |
q |
1 . |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
34

Неравенство (28) равносильно неравенству un 1 un , т.е. члены строго положительного ряда не убывают, а потому не могут стремиться к нулю (нарушено необходимое условие сходимости (14)). Ряд расходится.
Теорема доказана. |
|
|
|
|
|
|||||
|
|
Замечание 8. Неравенство |
(27) |
нельзя заменить на неравенство |
||||||
|
un 1 |
1. Действительно, для гармонического ряда при всех n |
||||||||
|
un |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
un 1 1 |
n 1 |
|
n |
1, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
un |
|
|
1 n |
|
n 1 |
||
|
|
|
|
|
||||||
но, как доказано ранее, гармонический ряд (12) расходится (см. пункт 2). Обычно чаще применяется другая (предельная) форма этого
признака.
Теорема 6 (предельный признак Даламбера). Пусть в случае стро-
го положительного ряда существует предел
lim |
un 1 |
D . |
(29) |
|
un |
||||
n |
|
|
Тогда
1)при D 1 ряд сходится;
2)при D 1 ряд расходится;
3)при D 1 ряд может как сходиться , так и расходиться (признак ответа не даёт).
Доказательство. Условие (29) по определению предела последовательности означает следующее: для любого 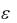 0 найдётся такой номер N , что для всех n N будут выполнены неравенства
0 найдётся такой номер N , что для всех n N будут выполнены неравенства
D |
|
un 1 |
D |
. |
|
un |
|||
|
|
|
|
|
В случае D 1 число D |
будет играть роль числа q в предыдущей |
|||
теореме (см. (27)). Действительно, в этом случае в силу произвольности
числа |
0 его можно выбрать таким, чтобы выполнялось неравенство |
q D |
1 ( за положительное число можно взять любое число, мень- |
шее чем 1 D ). Следовательно, по теореме 5 ряд сходится.
35

Если D 1, то, взяв |
D 1, |
получим, что D |
1. Тогда для |
|||
n N будет выполнено неравенство |
un 1 |
1 |
(см. (28)). По теореме 5 ряд |
|||
un |
||||||
|
|
|
|
|
||
расходится.
Покажем, что при D 1 ряд может как сходиться, так и расходиться. Приведём по этому случаю примеры. Так, для гармонического ряда
un |
1 |
имеем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
lim |
1 |
n |
1 |
lim |
|
n |
|
|
1. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
1 n |
|
|
|
n |
1 |
||||||||||
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
||||||
Рассмотрим теперь ряд с общим членом un |
1 |
. И в этом случае D 1: |
|||||||||||||||||
|
n2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
D |
lim |
1 |
|
n |
1 |
2 |
|
lim |
|
n2 |
|
1. |
|||||
|
|
|
|
1 n2 |
|
|
|
|
|
1 2 |
|
||||||||
|
|
|
n |
|
|
|
|
n |
|
n |
|
|
|||||||
Но гармонический ряд расходится, а ряд |
|
1 |
|
сходится (см. пример 18). |
|||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n 1 n2 |
|
|
|
|
||||
Признак Даламбера целесообразно применять, когда общий член ря-
да содержит выражения видов an , n! 1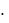 2
2 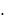 3
3 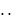
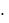 n .
n .
|
|
|
|
|
|
|
2n |
|
|
|
|
|
|
|
||
Пример 23. Исследуем ряд |
n 1 |
|
. Известно, что |
|
|
|
||||||||||
n! |
|
|
|
|||||||||||||
|
|
|
|
lim un |
|
|
lim |
2n |
|
0 , |
|
|
|
|||
|
|
|
|
|
|
|
n! |
|
|
|
||||||
|
|
|
|
n |
|
|
n |
|
|
|
|
|
||||
т.е. необходимое условие сходимости ряда |
выполнено. |
Найдём D |
||||||||||||||
согласно (29): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n 1 |
2n |
|
|
|
2n 1 |
n! |
|
2 |
|
0 . |
||||
D |
lim |
|
: |
|
|
lim |
|
|
|
|
|
lim |
|
|
||
|
|
|
|
n 1 ! 2n |
|
|
||||||||||
|
n |
n 1 ! n! |
n |
|
|
n |
n 1 |
|
||||||||
Так как D 0 |
1, то данный ряд по теореме 6 сходится. |
|
|
|
||||||||||||
36

Пример 24. Исследуем на сходимость ряд |
4n n! |
. Найдём |
D : |
|||||||||||||||
nn |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
||||
|
|
|
|
4n 1 n 1 ! |
|
4n |
n! |
|
n |
n |
4 |
|
|
|||||
|
D |
lim |
: |
4 lim |
|
. |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
n 1 n 1 |
|
nn |
|
n 1 |
|
e |
|
||||||||||
|
|
|
n |
|
|
n |
|
|
|
|||||||||
Так как D |
4 |
1, то данный ряд расходится. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
e |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Теорема 7 ( признак Коши). Пусть для ряда (22) для всех |
n или |
|||||||||||||||||
начиная с некоторого номера N выполнено условие |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
n un |
q |
1. |
|
|
|
|
|
|
(30) |
|||||
Тогда ряд сходится. Если же для всех n или, по крайней мере, с некоторого номера справедливо неравенство
|
|
|
|
|
|
n u |
n |
1 , |
(31) |
||
|
|
|
|
||
то ряд (22) расходится. |
|
|
|
|
|
Доказательство. Неравенство |
(30) равносильно |
неравенству |
|||
un qn , а (31) – неравенству un 1. Сравнение надо проводить со сходя-
щимся рядом |
qn q 1 |
и расходящимся рядом |
1. Если неравенства |
n |
1 |
n |
1 |
выполняются для всех n , |
то утверждения следуют из признака сравнения |
||
(теорема 3). Если эти неравенства выполняются только начиная с некоторого номера, то надо воспользоваться замечанием 7. В случае (31), равносильном неравенству un 1, расходимость ряда (22) следует и из того, что нарушено необходимое условие сходимости (14). Теорема доказана.
|
Замечание 9. Как и в теореме 5, неравенство (30) нельзя заменить на |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||
неравенство n un 1. Действительно, |
для гармонического ряда для всех |
||||||||||||||
|
|
|
|
n |
|
|
n |
|
1 |
|
|
|
1 |
|
|
n 2 |
имеет место неравенство |
un |
|
|
|
|
1, но гармонический ряд |
||||||||
n |
|
|
|
1 |
|
||||||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
n |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
расходится.
При решении примеров, как и в случае признака Даламбера, обычно применяют другую (предельную) форму признака.
37

Теорема 8 (предельный, или радикальный признак Коши). Пусть для положительного ряда (22) существует предел
|
|
|
|
|
lim n u |
n |
K . |
(32) |
|
n |
|
|
||
|
|
|
||
Тогда
1)при K 1 ряд сходится;
2)при K 1 ряд расходится;
3)при K 1 возможны как сходимость, так и расходимость ряда. Доказательство. На основании определения предела последователь-
ности условие (32) означает следующее: для любого 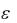 0 найдётся такой номер N , что для всех n N будут выполнены неравенства
0 найдётся такой номер N , что для всех n N будут выполнены неравенства
K 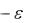 n
n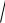 un K
un K 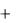 .
.
Далее доказательство такое же, как и в случае доказательства теоремы 6 – предельного признака Даламбера. При K 1 или K 1 выводы следуют из теоремы 7. То, что в случае K 1 признак не даёт возможности судить о поведении ряда, можно проверить на тех же двух примерах (гармонического ряда и обобщённого гармонического ряда с 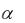 2 ), указанных при изучении предельного признака Даламбера. Для этого надо установить, что
2 ), указанных при изучении предельного признака Даламбера. Для этого надо установить, что
lim |
n |
|
1 |
|
1 и lim n |
|
1 |
|
1. |
n |
|
n2 |
|||||||
n |
|
|
|
n |
|
|
|||
Вычислим только первый из этих пределов, так как второй получится из первого на основании равенства
|
|
n |
|
1 |
|
|
|
n |
|
1 |
|
n |
|
1 |
|
|
|
|
|
|
|
|
|||
|
|
n2 |
n |
n . |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Для вычисления первого предела (неопределённость вида 00 ) рас- |
|||||||||||||||||||||||||
|
|
1x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
смотрим выражение y |
1 |
|
x |
1 |
|
|
|
с непрерывной переменной |
x 0 . |
||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||
x |
|
|
|
|
x |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|||||||||||||||||||
Прологарифмируем это выражение и докажем, что lim |
ln x |
1 |
0. |
Дей- |
|||||||||||||||||||||
x |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||
38
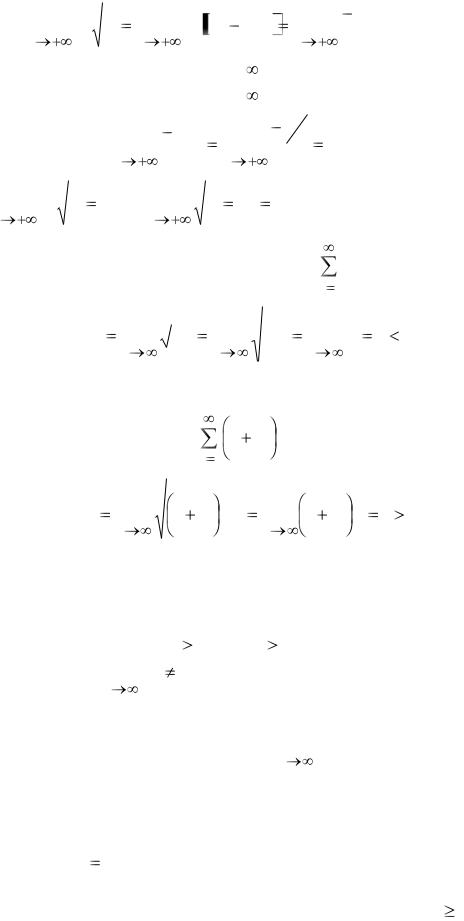
ствительно, |
lim ln x |
|
1 |
|
lim |
1 |
|
ln1 |
|
ln x |
|
|
|
lim |
|
|
|
|
ln x |
. Для вычисления |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
x |
|
|
|
||
последнего предела (неопределённость |
|
|
|
|
) применим правило Лопиталя: |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
ln x |
|
|
lim |
|
|
|
|
|
|
1x |
0 . |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Так как lim |
ln x |
1 |
|
|
0, то |
lim x |
1 |
|
|
e0 |
|
|
|
|
1. Теорема доказана. |
||||||||||||||||||||||||||||||||||
x |
x |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n |
|
|
|
|||
Пример 25. Исследуем на сходимость ряд n |
|
1 |
|
|
|
. Так как |
|||||||||||||||||||||||||||||||||||||||||||
|
nn |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
||
|
|
|
|
|
K |
|
|
|
|
lim |
n u |
n |
|
|
|
|
|
|
lim n |
|
lim |
|
0 |
1, |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
nn |
|
|
n |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
то этот ряд сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 26. Исследуем ряд |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
. Так как |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
n 1 |
|
|
n |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
|
|
|
||||||||
|
|
|
|
|
K |
|
|
|
|
lim |
n 1 |
|
|
|
|
|
|
|
|
|
lim |
1 |
|
|
|
|
|
|
e |
1, |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
то данный ряд расходится.
Сделаем несколько замечаний по поводу признаков Даламбера и
Коши. |
|
Замечание 10. Случаи D |
1 или K 1 (ряд расходится) фактически |
сводятся к тому, что lim un |
0 , т.е. не выполнено необходимое условие |
n |
|
сходимости ряда (проверьте это на примерах 24 и 26). Но иногда проще
вычислить D или K , чем находить предел lim un (это видно на примерах |
||
|
|
n |
24 и 26). |
|
|
Рассмотрим ещё один, достаточно простой пример. Покажем, что ряд |
||
|
nn |
|
с общим членом un |
|
расходится. Методом математической индукции |
|
||
|
n! |
|
можно установить, что для всех n выполняется неравенство nn n!. Тогда
39

un |
nn |
1 и, следовательно, lim un 0 ; ряд расходится. Этот вывод |
|
n! |
|||
|
n |
намного быстрее можно получить с помощью предельного признака Даламбера. Действительно
|
|
|
|
|
un 1 |
|
|
|
|
n 1 n 1 n! |
|
|
|
|
|
|
n 1 |
n |
|
|
|
|
|||||||||
|
|
D |
lim |
|
|
lim |
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
e |
1. |
|
|
|
||||||
|
|
un |
|
|
n 1 ! nn |
|
|
|
n |
|
|
|
|||||||||||||||||||
|
|
|
|
n |
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
||||||||||||
Так как D |
1, то ряд расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Замечание 11. В то же время с помощью признаков Даламбера и |
|||||||||||||||||||||||||||||||
Коши можно доказать, что |
lim un |
0 , если это равенство не очевидно. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Докажем, например, что |
lim |
an |
|
0 |
при любом a |
|
0 . Для этого рассмот- |
||||||||||||||||||||||||
|
n! |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
рим положительный ряд с общим членом un |
|
an |
|
a |
0 Вычислим D |
||||||||||||||||||||||||||
|
|
n! |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
по формуле (29): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
D lim |
an |
1 n! |
|
lim |
|
|
a |
|
|
|
0 |
1. |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
1 ! an |
|
|
n |
1 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
n |
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||||||||
Согласно теореме 6 данный ряд сходится. Тогда по теореме 1 |
lim un 0 , |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
т.е. lim |
an |
|
0 a |
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Замечание 12. Строго положительный ряд будет расходиться и в том |
|||||||||||||||||||||||||||||||
случае, если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
lim |
un |
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
(33) |
|||||
|
|
|
|
|
|
|
|
|
un |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Действительно, условие (33) означает, что |
un |
1 |
|
|
есть бесконечно большая |
||||||||||||||||||||||||||
|
un |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
величина. Тогда для любого E |
0 (в частности, для E |
1) найдётся |
такой |
||||||||||||||||||||||||||||
номер |
N , что для всех |
n |
N |
будет выполняться неравенство |
un |
1 |
1. |
||||||||||||||||||||||||
un |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Остаётся обратиться к теореме 5 (см. (28)); при этом и общий член ряда не стремится к нулю.
40
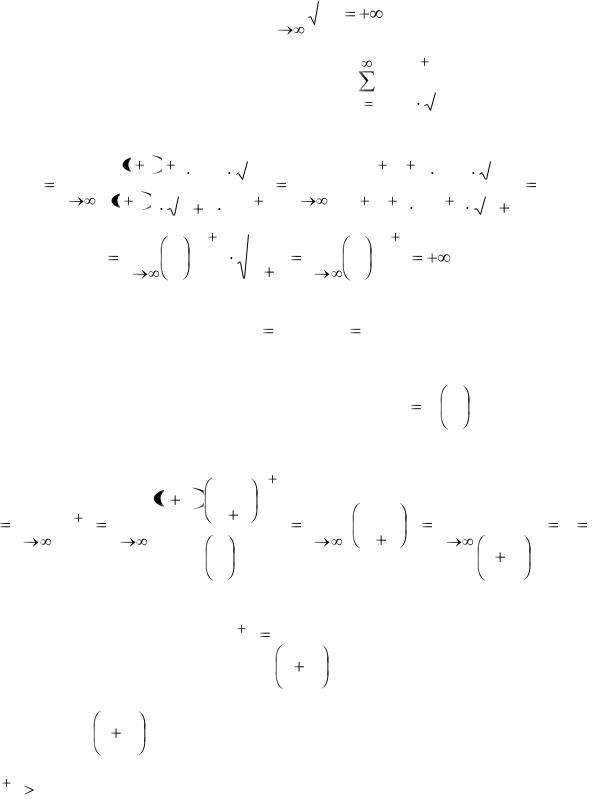
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Положительный ряд в случае |
|
lim n u |
n |
|
|
|
|
|
|
|
также расходится. |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Пример 27. Выяснить, сходится ли ряд |
|
|
|
|
|
|
5n2 |
1 |
|
|
. Находим D по |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
n |
1 2n2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
формуле (29): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
5 n 1 2 1 2n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5n2 |
|
|
2n 2 2n2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
D |
|
lim |
|
|
n |
|
|
|
|
lim |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 n 1 2 |
|
|
|
|
|
|
5n2 |
|
2n2 |
2n 1 5n2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
n 1 |
|
|
|
|
|
n 1 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
lim |
5 |
|
|
|
|
|
n |
|
lim |
|
5 |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
n |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Согласно замечанию 12 данный ряд расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
Замечание 13. В случаях D |
|
|
1 или K |
|
1 предельные признаки от- |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
вета не дают. По соответствующему непредельному признаку ответ иногда |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
для ряда с общим членом un |
n! |
|
|
e |
n |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
можно получить. Так, |
|
|
|
|
|
|
предельный |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
признак Даламбера не годится, так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
n |
1 ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
un 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
e |
|
|
e |
|
|
||||||||
|
D |
|
lim |
|
|
lim |
|
n |
1 |
|
|
|
|
|
|
|
|
lim e |
|
|
|
|
|
lim |
|
|
|
|
|
|
1. |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
un |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
1 |
|
|
|
|
|
|
|
|
n |
e |
||||||||||||||||||||||||
|
|
n |
|
|
n |
|
|
|
|
|
e |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
1 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Однако в рассматриваемом случае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
un |
1 |
|
|
|
|
|
|
|
e |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
un |
1 |
|
1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и поскольку |
1 |
|
1 n |
стремится к пределу |
|
e , |
|
монотонно возрастая, |
то |
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
un |
1 |
1 |
для всех n . Таким образом, выполнено условие (28) непредельно- |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
un
го признака Даламбера и ряд расходится.
При решении примеров предельный признак Даламбера более употребителен, чем предельный признак Коши. Это объясняется тем, что вычислить D по формуле (29) часто легче, чем K по формуле (32) (напри-
41

мер, в случае наличия выражений с факториалами). Однако признак Коши сильнее признака Даламбера. Во всех случаях, когда применим признак Даламбера, ответ может быть получен и с помощью признака Коши. Обратное утверждение неверно. Имеются примеры рядов, когда признак Коши действует, а признак Даламбера – нет. Примером такого ряда является
ряд с общим членом un |
1 n |
|
3 |
. Читатель легко может убедиться, что в |
|
2n |
1 |
|
|
||
|
|
|
|
||
этом случае предел (29) вообще не существует. Предел же (32) существует,
при этом K |
1 |
; следовательно, по предельному признаку Коши ряд с та- |
|
2 |
|||
|
|
ким общим членом сходится.
Имеются ряды, к которым оба вышеописанных признака не применимы. Так, например, с помощью этих признаков нельзя ответить на вопрос о сходимости обобщённого гармонического ряда (13) при любом ве-
щественном числе |
. Действительно, |
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
D lim |
|
un |
1 |
lim |
n 1 |
lim |
n |
|
1, |
|
un |
|
1 |
n 1 |
|||||
n |
|
|
n |
n |
|
||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
n |
|
1 |
|
|
|
|
K |
|
lim n u |
n |
lim n |
|
lim |
1 1. |
||||||||||
|
|
n |
||||||||||||||||
|
|
|
|
|
n |
n |
n |
|
n |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
||||||||||||||
(то, что lim n |
1 |
|
1 было установлено ранее). Для этого ряда пока лишь |
|||||||||||||||
n |
||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
установлено, что он расходится при 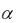 1 (см. пункты 2 и 3). Вопрос о сходимости ряда (13) при
1 (см. пункты 2 и 3). Вопрос о сходимости ряда (13) при 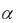 1 остаётся открытым.
1 остаётся открытым.
Изучим ещё один признак сходимости положительных рядов, который и даст ответ на вопрос о сходимости ряда (13) при всех 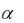 (в частности, при
(в частности, при 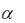 1). Этот признак основан на интегральном исчислении. Для этого напомним понятие несобственного интеграла по бесконечному промежутку интегрирования.
1). Этот признак основан на интегральном исчислении. Для этого напомним понятие несобственного интеграла по бесконечному промежутку интегрирования.
42

Пусть функция f x непрерывна на промежутке a, |
. Тогда она |
|||
интегрируема на любом отрезке |
a,b , где b |
a . Несобственный интеграл |
||
f x dx определяется равенством |
|
|
|
|
a |
|
|
|
|
|
|
b |
|
|
f x dx |
|
lim f |
x dx . |
|
a |
b |
a |
|
|
|
|
|
||
Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится; в противном случае несобственный интеграл называется
расходящимся. Если при этом для |
f x существует первообразная функ- |
||||
ция F x |
на всем промежутке |
a, |
, то справедлива формула |
||
|
|
|
|
||
|
f x dx |
F |
F a F x |
|
a , |
|
a |
|
|
||
|
|
|
|
|
|
где F |
lim F x . Эта формула является аналогом формулы Ньюто- |
||||
|
x |
|
|
|
|
на-Лейбница для определённого интеграла по отрезку a,b от непрерывной функции f x .
от непрерывной функции f x .
Теорема 8 (интегральный признак Маклорена – Коши). Пусть за-
данная на промежутке 1,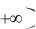 функция f x
функция f x непрерывна, неотрицательна и не возрастает. Пусть положительный числовой ряд имеет форму
непрерывна, неотрицательна и не возрастает. Пусть положительный числовой ряд имеет форму
un |
f x , |
(34) |
n 1 |
n 1 |
|
т.е. члены ряда удовлетворяют условию
u1 f 1 , u2 f 2 , 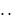
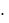 , un f n ,
, un f n , 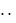 .
.
Тогда для сходимости ряда (1.34) необходимо и достаточно, чтобы сходился несобственный интеграл
|
f |
x dx . |
(35) |
|
1 |
|
|
Доказательство. В силу монотонности функции f x |
на любом от- |
||
резке n, n 1 n 1, 2, ... |
справедливы неравенства |
|
|
un |
f n f x |
f n 1 un 1. |
|
|
|
43 |
|
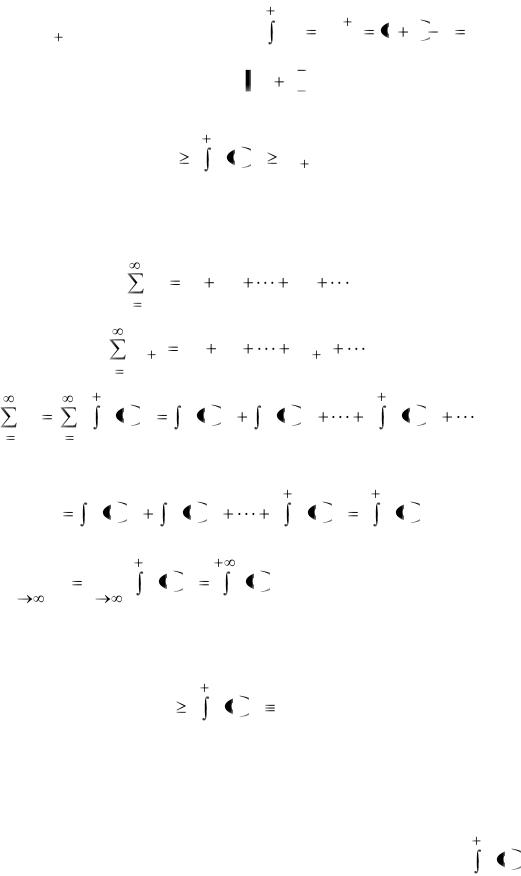
|
n |
1 |
|
|
nn 1 |
|
Так как un , un 1 – постоянные числа и |
1 dx |
x |
|
n 1 n 1, то, ин- |
||
|
||||||
|
|
|
||||
|
n |
|
|
|
|
|
тегрируя эти неравенства по отрезку n, n |
1 , из свойств неопределённого |
|||||
интеграла получим |
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
un |
f x dx |
un |
1 . |
|
|
(36) |
|
n |
|
|
|
|
|
Неравенства (36) позволяют обратиться к признаку сравнения (теорема 3) для следующих рядов:
|
|
|
|
un |
u1 |
u2 |
|
un |
, |
|
|
(37) |
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
un |
1 |
u2 |
u3 |
|
un |
1 |
, |
|
(38) |
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
2 |
|
3 |
|
|
n |
1 |
|
|
vn |
|
f |
x dx |
|
f |
x dx |
f |
x dx |
|
|
f x dx |
. (39) |
n |
1 |
n |
1 n |
|
|
1 |
|
2 |
|
|
|
n |
|
Рассмотрим ряд (39). Его n -й частичной суммой будет |
|
||||||||||||
|
|
|
2 |
|
3 |
|
|
|
n 1 |
|
n |
1 |
|
|
|
Sn |
f x dx |
|
f x dx |
|
f x dx |
|
f x dx . |
|
|||
|
|
|
1 |
|
2 |
|
|
|
n |
|
1 |
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
Так как |
lim Sn |
lim |
f |
x dx |
f |
x dx , то в силу определения 3 схо- |
|||||||
|
n |
|
n |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
димость ряда (39) означает сходимость несобственного интеграла (35). |
|||||||||||||
Если ряд (37) сходится, то по признаку сравнения рядов в силу пер- |
|||||||||||||
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
вого неравенства из (36) un |
|
f x dx |
vn будет сходиться ряд (39) и, |
||||||||||
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
следовательно, несобственный интеграл (35). Первая часть теоремы доказана, т.е. установлено необходимое условие сходимости.
Пусть сходится несобственный интеграл (35). В силу ранее отмечен-
n 1
ного будет сходиться и ряд (39), общий член которого имеет вид f x dx .
n
Тогда на основании признака сравнения рядов в силу второго из (36) нера-
44

n |
1 |
венства un 1 |
f x dx будет сходиться ряд с меньшими членами, т.е. |
|
n |
ряд (38). Поскольку ряд (37) отличается от ряда (38) только первым членом u1 , то на основании замечания 4 будет сходиться и ряд (37), т.е. исходный ряд (34). Достаточное условие установлено. Теорема доказана.
Теорема 8 означает, что ряд (34) и несобственный интеграл (35) одновременно сходятся или расходятся.
Пример 28. Исследуем на сходимость обобщённый гармонический
ряд (13). При |
0 ряд расходится, поскольку общий член при таких не |
|||
стремится к нулю. Остаётся рассматривать случай |
0. При таких |
|||
функция f x |
1 |
на промежутке 1, |
непрерывна, |
положительна и |
|
||||
|
||||
x
монотонно убывает, т.е. удовлетворяет условиям теоремы 8, причём
f n 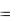 1 . Значит, исследуемый ряд (13) сходится или расходится одно- n
1 . Значит, исследуемый ряд (13) сходится или расходится одно- n
временно с несобственным интегралом |
1 |
dx . Исследуем на сходи- |
|
1 x
мость этот интеграл при 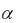 0.
0.
При 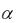 1 функция f x
1 функция f x имеет вид f x
имеет вид f x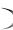 1x , а её первообразной на промежутке 1,
1x , а её первообразной на промежутке 1,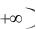 является функция F x
является функция F x ln x . Тогда
ln x . Тогда
|
1 |
dx ln x |
|
1 |
ln |
ln1 |
, |
|
|
||||||
|
|
|
|||||
1 x |
|
|
|
|
|
||
|
|
|
|
|
|||
т.е. несобственный интеграл расходится. Следовательно, гармонический ряд (12) расходится, что было установлено и ранее другими методами (см. пункт 2).
|
При |
1 |
первообразной функции f x |
1 |
будет функция |
|
|
|
|||||
|
x |
|||||
|
|
|
|
|
|
|
F x |
1 |
x |
1 . Тогда |
|
|
|
|
|
|
|
|||
1 |
|
|
||||
|
|
|
|
|
||
45

|
|
|
1 |
dx |
|
1 |
|
1 |
|
. |
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|||
|
|
1 |
x |
|
x |
1 |
|
|
|
|
||||
Если 0 |
1 |
1 |
0 , |
|
то F |
|
|
|
lim |
1 |
x1 |
. В |
||
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
x |
|
|
||
этом случае несобственный интеграл расходится, а тем самым расходится и соответствующий ряд (расходимость при таких была установлена другим способом в пункте 3).
|
Если же |
1 |
1 |
|
0 , то F |
|
|
lim |
1 |
|
|
1 |
|
0 |
. Тогда |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
1 |
|
|
|
1 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
x |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
dx F |
F 1 |
0 |
1 |
|
|
1 |
|
, т.е. |
интеграл конечен (сходит- |
|||||||||
|
|
|
|
|
|
|
|
|||||||||||||
1 x |
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||
ся). Следовательно, сходится и соответствующий ряд.
Таким образом, для обобщённого гармонического ряда (13) справедливо утверждение: ряд сходится при 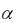 1 и расходится при
1 и расходится при 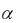 1. Теперь этим рядом (при всех ) можно пользоваться для сравнения с ним других рядов при применении теоремы 3.
1. Теперь этим рядом (при всех ) можно пользоваться для сравнения с ним других рядов при применении теоремы 3.
В связи с изучением ряда (13) отметим следующее. В математике очень известна так называемая дзета-функция Римана, определённая равенством
1 . n 1 n
Эта функция была введена Эйлером, а для комплексных значений аргумента её поведение исследовал Риман.
Пример 29. Исследуем на сходимость ряд |
1 |
|
|
|
. Очевидно, что |
||||||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
n 1 n2 |
1 |
|
|
|
|
|
|
|
||||
в качестве функции теоремы 8 надо взять функцию |
f x |
1 |
|
|
. Так как |
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
x2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||
несобственный интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
dx arctgx |
|
1 |
arctg |
arctg1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 x2 |
|
2 |
|
4 |
|
|
4 |
|
|
||||||||||
1 |
|
|
|
|
|
|
|
|
|
||||||||||
46
