Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Хабаровский государственный университет экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5510.pdf

Скачиваний:

Добавлен:

13.11.2022

Размер:

1.67 Mб

Скачать

☆

1 / 91 2 3 4 5 6 7 8 9 > Следующая >>>

Министерство образования и науки Российской Федерации

Государственное образовательное учреждение высшего профессионального образования

«Хабаровская государственная академия экономики и права»

Кафедра математики и математических методов в экономике

М.Ф. Тиунчик, Е.О. Старкова, С.В. Тонконог

Математический анализ

Числовые ряды

Хабаровск 2011

ББК В Т 45

Тиунчик М. Ф. Математический анализ. Числовые ряды : учеб. пособие / М. Ф. Тиунчик, Е. О. Старкова, С. В. Тонконог. – Хабаровск : РИЦ ХГАЭП, 2011. – 72 с.

Содержание учебного пособия соответствует государственным образовательным стандартам дисциплины «Математический анализ» по изучению раздела «Числовые и функциональные ряды». Для выполнения индивидуальных заданий по данной тематике можно использовать методическую разработку авторов [8].

Пособие предназначено для бакалаврантов и магистрантов по направлениям подготовки «Экономика», «Менеджмент», «Торговое дело», «Сервис», «Туризм», «Государственное и муниципальное управление», «Товароведение», «Прикладная информатика».

Рецензенты: А. И. Ивлева, канд. физ.-мат. наук, доцент Хабаровского пограничного института Федеральной службы Российской Федерации; Е. В. Карачанская, канд. физ.-мат. наук, доцент кафедры прикладной математики ТОГУ

Утверждено издательско-библиотечным советом академии в качестве учебного пособия

Тиунчик М.Ф, Старкова Е.О., Тонконог С.В., 2011 Хабаровская государственная академия экономики и права, 2011

Введение

Числовые и функциональные ряды – один из важных разделов дисциплины «Математический анализ». Теория рядов основана на знании двух других разделов этой дисциплины – дифференциального и интегрального исчислений. Общей же базой при изучении всех трёх разделов является теория пределов.

Изучение теории рядов студентами экономических направлений и специальностей необходимо в связи с её применением при решении важнейших задач не только в самом математическом анализе (приближённые вычисления значений функций и интегралов с достаточной степенью точности) и в дифференциальных уравнениях (их интегрирование с помощью рядов), но и в различных экономико-математических дисциплинах (временные ряды).

Данное учебное пособие посвящено только изучению числовых рядов. Изучение функциональных рядов планируется в отдельном издании. Материал содержит как общие положения теории числовых рядов, так и вопросы, связанные с положительными и знакопеременными рядами. По всем темам имеются подробные теоретические сведения в основном с их доказательством. Напоминаются основные понятия из теории пределов, при необходимости читатель может обратиться, например, к учебному пособию [4].

Теоретический материал сопровождается рассмотрением разнообразных примеров для каждой определённой ситуации. Изложение материала ведётся на доступном, по-возможности строгом языке. В конце каждого раздела приведён набор задач для аудиторной и самостоятельной работы, а также список теоретических вопросов для самоконтроля.

Нумерация пунктов, теорем, определений, замечаний, примеров и формул в теоретической части – сплошная; отдельная нумерация – в упражнениях и вопросах для самопроверки к каждой изучаемой теме. При ссылках указывается номер соответствующего пункта, теоремы, определения, замечания, примера.

Пособие рассчитано на студентов очной и заочной форм обучения. Студент может считать материал усвоенным, если сможет выполнять

предложенные упражнения и отвечать на вопросы для самоконтроля. Настоящее учебное пособие может быть использовано для всех эко-

номических направлений и специальностей, так как в нём отражены все вопросы, предусмотренные по данному разделу соответствующими государственными стандартами. Кроме того, студенты бакалавриата по направлению «Менеджмент» по профилю «Управление проектами» могут пользоваться данным пособием для более подробного изучения данной темы. Данное пособие может быть рекомендовано преподавателям для подготовки к лекционным и практическим занятиям.

1 Основные понятия

До сих пор в основном рассматривались алгебраические суммы, состоящие из конечного числа слагаемых, являющихся действительными (вещественными) числами или функциями одной действительной пере-

менной. Примерами таких сумм являются:

1) сумма

конечного

числа

членов

арифметической

прогрессии

a, a

d , a

2d ,

, a

1 d с

первым

членом

a , n -м

членом

a n

1 d и разностью d этой прогрессии;

2) сумма

конечного

числа членов

геометрической

прогрессии

a, aq, aq2 ,

, aqn 1 с первым членом u

0 ,

n -м членом u

aqn 1 и

знаменателем q

0 этой прогрессии;

3) сумма

a x

n 1

xn a

0 ,

составлен-

ная из произведений действительных коэффициентов a0, a1, ... , an

на сте-

пенные функции x0 , x1, x2 ,

, xn

целых неотрицательных степеней дей-

ствительной переменной x и называемая многочленом (полиномом) степе-

ни n 0 или целой рациональной функцией.

Как известно, в первом примере эта сумма есть число

Sn	u1	un n				an			1	n n 1 d ,											(1)
Sn		2				an		2		n n 1 d ,											(1)
		2						2
а во втором – число
	Sn	a	1		qn			q 1 .													(2)
	Sn	a		1	q			q 1 .													(2)
				1	q
Рассмотрим ещё одну сумму из n слагаемых 1,													1	,	1	,	1	,	,	1	:
Рассмотрим ещё одну сумму из n слагаемых 1,													2	,	3	,	4	,	,	n	:
													2		3		4			n
Sn		1	1		1		1				1	.									(3)

			2		3		4
			2		3		4				n
Для неё известна формула
		Sn		ln n			c		n ,												(4)

{1, 2, 3,

где n	– некоторая бесконечно малая величина lim	n 0 , а c есть по-
	n

стоянное положительное число, называемое постоянной Эйлера ( c 0,577215 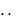). Последнее равенство показывает лишь, что с возрастанием n сумма Sn растёт, как ln n .

В различных приложениях математического анализа сталкиваются с выражениями, содержащими бесконечное число слагаемых. Например, с выражением, слагаемые которого являются членами бесконечной геометрической прогрессии. Такие выражения называются рядами: числовыми, если членами являются действительные числа; функциональными, если членами являются функции действительной переменной. Такого рода ряды и изучаются в настоящем пособии. Отметим, что применяются и ряды, членами которых являются комплексные числа или функции комплексной переменной.

Итак, рассмотрим бесконечную числовую последовательность (или

просто последовательность)
u1, u2 , , un ,	,	(5)

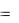
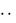
членами (элементами) которой являются действительные числа. Это означает, что каждому номеру n (числу из множества N , n, } натуральных чисел) поставлено в соответствие одно и только одно действительное число un , называемое n -м членом последовательности (5). Можно сказать, что последовательность есть функция натурального аргумента (областью определения всегда является множество N ). Правило (закон) f соответствия может быть различным для разных аргументов n .

Часто встречающейся является ситуация, когда un зависит от n по одному

и тому же закону f для всех n : un	f n . Тогда un можно назвать общим
членом числовой последовательности	(5).

Поясним сказанное примерами. Рассмотрим заданные общими членами следующие последовательности:

1)un	n ,	2) un n2 , 3) un		1		, 4) un		( 1)n 1	, 5)	un ( 1)n 1,
1)un	n ,	2) un n2 , 3) un			n	, 4) un		n	, 5)	un ( 1)n 1,
					n			n
6) un	1 ( 1)n 1 , 7)		1 (	1)n		1	.
			un
			un	n
				n

В развёрнутом виде эти последовательности таковы:

1)1, 2, 3, 4, 5, , n, ; 2)1, 4, 9, 16, 25, , n2 , 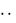; 3)1, 12 , 13 , 14 , 15 ,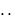 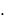, 1n , ;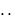


4)1,		1		,		1	,		1	,	1		,		,		(		1)n	1	,	;
4)1,		2		,	3		,		4	,	5		,		,				n		,	;
		2			3				4		5								n
5)1, 1,1,							1,1,					, (			1)n				1,	;
6)	2, 0, 2, 0, 2, 0,													,1		(			1)n	1,		;
7)	2, 0,		2		, 0,			2	, 0,			2		,		,		1	(	1)n		1	, .
7)	2, 0,		3		, 0,			5	, 0,			7		,		,				n			, .
			3					5				7								n

Таким образом, все члены приведённых в примерах последовательностей получались из единого аналитического выражения – формулы общего члена.

Рассмотрим ещё два примера конкретно заданных последовательностей:

1)1, 12 , 13 , 14 , 25, 36, 49, 64, 27, 30, 33, 36, 39, 42, ; 2) 2, 3, 5, 7,11,13,17,19, 23, .

Для первой последовательности по закономерности расположения её членов можно предположить, что

	1			при	1	n	4,

		n

un	n		2	при	5	n	8,

	3n			при	n	9.

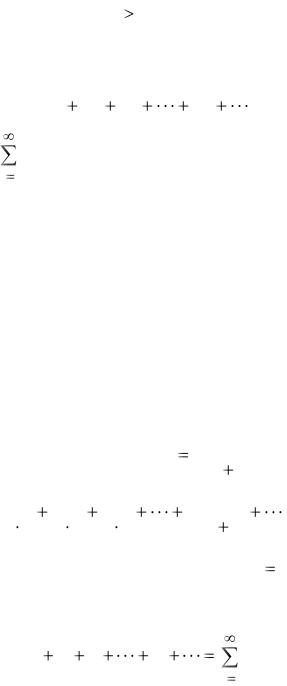
Таким образом, эта последовательность для различных номеров n задаётся различными аналитическими формулами. Вторая последовательность не имеет аналитического выражения для нахождения по номеру n её членов,

это	есть последовательность так называемых простых чисел (простое чис-
ло	– это натуральное число	p 1,	имеющее	только два делителя –
1 и само p ).
	Определение 1. Выражение вида
	u1 u2	u3	un	(6)

(в краткой записи un ), состоящее из суммы членов бесконечной число-

n 1

вой последовательности (5), называется числовым рядом (или просто

рядом).

Элементы un , из которых образовано выражение (6), называют чле-

нами данного ряда.

В основном будут изучаться ряды, когда n -й член un задаётся для всех n единой аналитической формулой. Тогда un называют общим членом ряда. Ряд будет считаться заданным, если будет указана формула его общего члена un .

Пример 1. Ряд с общим членом un					1				имеет вид

						n(n	1)
						n(n	1)
1	1		1		1					.

1 2	2	3	3 4		n(n		1)
1 2	2	3	3 4		n(n		1)
Пример 2. Числовой ряд с общим членом un										1	называется гармо-
Пример 2. Числовой ряд с общим членом un										n	называется гармо-
										n
ническим и имеет вид
1	1	1	1					1	.
1									.
	2	3		n		n	1 n

Каждый член этого ряда, начиная со второго, представляет собой среднее гармоническое двух соседних его членов. Число c называется средним гармоническим чисел a и b , если выполняется равенство

S1, S2 ,

, Sn ,

									1	1		1				1	.
																	.
									c	2		a				b
					( 1)n 1					1					1				1			( 1)n 1
Пример 3.																											.
Пример 3.																											.
		n 1 n2 (n 2) 12 3 22																4 32 5				n2 (n 2)
Определение 2. Сумма первых n																	членов ряда (6) называется n-й
частичной суммой ряда и обозначается через Sn , т.е.
								Sn	u1		u2								un .				(7)
Пример 4.			Найдём первые три частичные суммы ряда																				1					.
																							n 1
																							n 1			n(n 1)
Так как согласно (7)
			S1			u1, S2			u1		u2 , S3								u1 u2	u3 ,
то в данном примере
S	1		1	, S			1			1			2	, S					1	1	1			3	.
S				, S		2								, S				3							.
1	1 2	2				2	1 2			2 3		3						3	1 2	2 3	3 4		4
	1 2	2					1 2			2 3		3							1 2	2 3	3 4		4

Очевидно, что с увеличением n частичные суммы (7) расширяются до формального ряда (6). Поскольку сложение бесконечного множества чисел не определено, то естественно будет назвать суммой ряда (6) предел последовательности

(8)

его частичных сумм. Известно, что любая числовая последовательность либо сходится (имеет конечный предел), либо расходится (имеет пределом 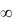или вообще не имеет никакого предела – ни конечного, ни бесконечного).

Определение 3. Если существует конечный предел S lim Sn по-

следовательности (8) частичных сумм ряда (6), то этот предел называют

суммой этого ряда (при этом записывают S		un ) и говорят, что ряд
	n	1
сходится. Если lim Sn	или вообще не существует, то ряд называется
n

расходящимся.

Если lim Sn										, то условно пишут															un						;	соответственно
			n																					n	1
																								n	1
un		, если lim Sn													.
n 1						n
n 1
Пример 5. Исследуем ряд n																				1			. Так как для всех n справед-

																			1 n(n			1)
ливо равенство				1						1					1		, то

					n n		1				n		n		1
Sn	1			1			1								1							1	1		1			1				1	1

	1 2 2 3 3 4														n(n 1)								2		2 3							3 4
	1 2 2 3 3 4														n(n 1)								2		2 3							3 4
										1		1						1				1		1	1				.

								n		1				n					n		n	1				n		1
Тогда	lim Sn				lim		1			1						1, т.е. ряд сходится; его сумма равна 1.

											n	1
	n				n						n	1
Пример					6. Докажем,											что			ряд				n	расходится.									Согласно		(1)
																						n 1
Sn 1			n		(n 1)n				. Следовательно,													lim Sn					lim			n(n			1)	.
Sn 1			n	2					. Следовательно,													lim Sn					lim							.
				2																		n				n					2
Это и означает, что данный ряд расходится. Можно считать, что																																		n	.
																																		n 1
Пример 7. Исследуем ряд 1																		1		1		1			( 1)n 1									( 1)n 1 .
																																	n	1
Последовательность его частичных сумм такова:
		S1		1, S2			0, S3							1, S4				0,				, S2n 1				1, S2n					0, .

Очевидно, что она не имеет предела. Данный ряд расходится.

Примерами 6 – 7 проиллюстрированы все три возможных ситуации определения 3.

Одной из задач теории рядов является установление их сходимости (или расходимости). Для этого в дальнейшем будут приведены признаки, с помощью которых (не прибегая к вычислению предела последовательно-

1 / 91 2 3 4 5 6 7 8 9 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.20221.64 Mб15505.pdf
#
13.11.20221.65 Mб175506.pdf
#
13.11.20221.66 Mб45507.pdf
#
13.11.20221.66 Mб25508.pdf
#
13.11.20221.66 Mб125509.pdf
#
13.11.20221.67 Mб55510.pdf
#
13.11.20221.67 Mб25511.pdf
#
13.11.20221.67 Mб15512.pdf
#
13.11.20221.67 Mб35513.pdf
#
13.11.20221.68 Mб15514.pdf
#
13.11.20221.68 Mб205515.pdf