5462

2

ББК В З-38

Захарова В.Н. Оптимизация транспортно-экономических связей: учеб. пособ. – Хабаровск: РИЦ ХГАЭП, 2005. – 104 с.

Рецензенты: канд.физ.-мат.наук, доцент кафедры прикладной математики ДВГУПС Е.Н. Ломакина; канд.физ.-мат.наук, старший научный сотрудник института экономических исследований ДВО РАН С.А. Ланец.

В учебном пособии рассмотрены различные проблемы оптимизации транспортно-экономических связей, постановки задач, их математические модели, алгоритмы решения. Даны решения типовых задач и задания для самостоятельного решения.

©В.Н. Захарова, 2005

©Хабаровская государственная академия экономики и права, 2005

3

Оглавление

Введение Глава 1. Классическая транспортная задача по критерию минимума издержек

Глава 2. Обобщенная транспортная задача (λ – задача) Глава 3. Транспортная задача с запретами Глава 4. Транспортная задача по критерию времени

Глава 5. Транспортные задачи с учетом времени и издержек Глава 6. Транспортные задачи по перевозке неоднородного взаимозаменяемого груза Глава 7. Транспортные задачи с ограничениями по пропускной способности

Глава 8. Двухэтапные производственно-транспортные задачи Глава 9. Задача оптимального размещения производства Глава 10. Транспортная задача в сетевой постановке Глава 11. Задача коммивояжера

Глава 12. Решение транспортной задачи на персональном компьютере с использованием ППП QM for Windows (Transportation)

4

Введение

Транспортные расходы при производстве и доставке продукции до потребителя являются значительной составляющей цены на продукцию, поэтому их снижение является одной из важнейших задач производства и реализации продукции.

Задача минимизации суммарных транспортных затрат по доставке продукции от поставщиков до потребителей решается по алгоритму метода потенциалов для классической транспортной задачи. В этой задаче предполагается, что перевозится однородная продукция, одним видом транспорта, по любому маршруту.

На практике условия задач значительно усложняются. Перевозимая продукция редко бывает однородной, перевозится различными видами транспорта, многие маршруты могут быть закрыты. В некоторых случаях доставка продукции осуществляется не непосредственно потребителю, а поэтапно – через переработку, склады, посредника и пр. Таким образом, возникают задачи по перевозке неоднородного груза, с запретами, многоэтапные.

Во многих задачах критерием оптимальности является минимальное время реализации доставки груза. Реализация решений задач по критерию минимума времени требует больших затрат, поэтому возникает задача минимизации затрат при минимальном времени реализации, то есть задача

сучетом времени и издержек.

Вданном учебном пособии рассмотрены математические постановки и алгоритмы решения:

-классической транспортной задачи;

-обобщенной транспортной задачи (λ – задачи);

-задачи с запретами;

-задачи по перевозке неоднородного взаимозаменяемого груза;

-двухэтапной производственно-транспортной задачи;

-задачи с ограничениями по пропускной способности;

-задачи оптимального размещения производства;

-транспортной задачи в сетевой постановке;

-транспортной задачи по критерию времени;

-транспортной задачи с учетом времени и издержек;

-задачи коммивояжера.

Вкаждой главе предложены вопросы для самопроверки и задачи для самостоятельного решения.

Вданном пособии рассматривается решение классической транспортной и некоторых других задач на компьютере с применением

ППП QM for Windows.

5

Глава 1. Классическая транспортная задача по критерию минимума издержек

Постановка задачи. На m станциях отправления A1 , A2 ,..., Ai, ..., Am имеется

Система ограничений (1.1) характеризует ограничения по ресурсам, (1.2) – ограничения по потребностям. Задача решается в таблице

6

то транспортная задача называется закрытой.

Если условие баланса не выполняется, то задача называется открытой и приводится к закрытой введением фиктивного поставщика с мощностью

Для фиктивного поставщика или потребителя Сij = 0.

Приведем необходимые для решения формулировки основных теорем транспортной задачи.

Теорема 1. (О разрешимости транспортной задачи). Транспортная задача при условии выполнения баланса всегда имеет оптимальное решение.

Система ограничений математической модели (1.1) – (1.2) имеет (m + n) уравнений и m · n неизвестных.

Доказано, что одно из уравнений является линейной комбинацией остальных, то есть является линейно зависимой и число базисных переменных системы равно (m + n -1).

Теорема 2. (О числе базисных переменных). Система ограничений транспортной задачи (1.1) – (1.3) содержит (m +n -1) линейно независимых уравнений.

Из этой теоремы следует, что невырожденный план транспортной задачи (все базисные переменные xij отличны от нуля) содержит (m + n –

1) базисных переменных, которым соответствуют занятые клетки в таблице решения.

Как и в симплексном методе при решении транспортной задачи необходимо найти первоначальный опорный план задачи. Рассмотрим на условном примере один из распространенных методов построения первоначального опорного решения (плана), учитывающих затраты на перевозки.

Метод наименьшего элемента матрицы С

Строительный песок добывается в четырех карьерах и доставляется на пять строительных площадок. Производительность карьеров за день составляет А1 – 100, А2 – 120, А3 – 80, А4 – 120 т песка. Потребность строительных площадок в песке В1 – 60, В2 – 100, В3 – 95, В4 – 125, В5 – 40 т. Затраты на добычу и доставку песка из карьеров до строительных площадок представлены матрицей

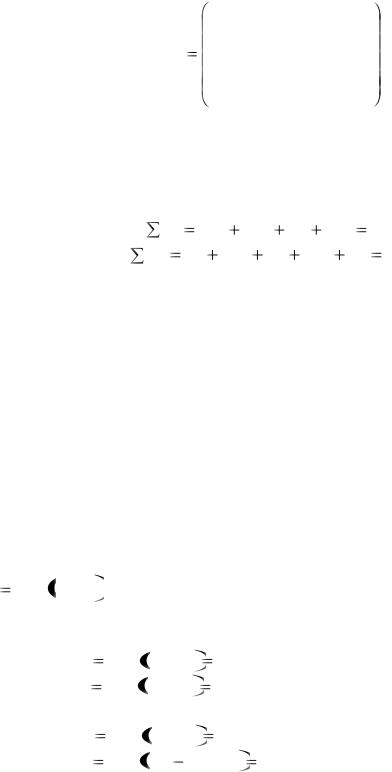
7

70 50 30 20 10

С

30 40 80 40 50

20 20 50 60 90

10 30 60 50 80

Найти оптимальную схему прикрепления строительных площадок к карьерам, при которой суммарные затраты на добычу и доставку сырья будут минимальными.

Решение. Карьеры представим поставщиками, строительные площадки

– потребителями. Проверим условие баланса

Условие баланса выполняется, следовательно, задача закрытого типа. Данные задачи представим в таблице

Первой в таблице заполняется клетка (i,j) с наименьшим Сij по правилу xij min ai , b j . Затем заполняются клетки в порядке возрастания Сij с

учетом предыдущих поставок. В нашем случае наименьший тариф имеют клетки (1,5) и (4,1). Выбираем любую, например (4,1), и ставим в неё

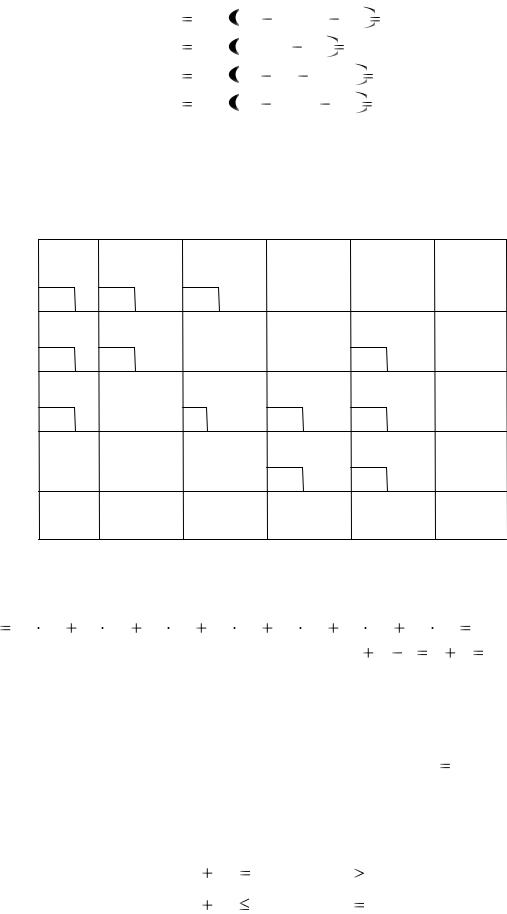
Следующими заполняются клетки в порядке возрастания Сij с учетом предыдущих поставок:

следует, что число заполненных клеток в таблице равно 8. Для решения задачи используем один из распространенных методов решения метод

оптимальным планом транспортной задачи (1.1) – (1.3), то ему соответствует система из (m + n) чисел ui* и v*j , удовлетворяющим условиям

10

Затем величину θ прибавляем к поставкам в вершинах со знаком плюс и отнимаем от поставок со знаком минус. Получаем новый опорный план

Система уравнений содержит 8 линейно независимых уравнений и 9 неизвестных, поэтому одно из неизвестных задаем произвольно, остальные рассчитываем из системы уравнений.

Полагаем u4 0 (по наибольшему числу занятых клеток в четвертой строке). Получаем

Для свободных клеток вычисляем характеристики Еij Cij (ui v j ) и записываем их в левых нижних углах.