5408

Информация о математическом ожидании и дисперсии величины S в

полностью её определяет, поэтому

и находится из таблиц функции Лапласа.

Значения параметра t в зависимости от гарантии безопасности даны в таблицы 5.2.

Таблица 5.2 – Таблица для вычисления показателя t

Итак, страховой фонд по заданному страховому портфелю найден.

Пройдём теперь к вычислению нетто-ставки Тн , которая в рисковых видах страхования рассчитывается со 100 рублей страховой суммы

Обозначим через S общую страховую сумму по всему страховому

82

Страховая сумма S выражается через среднюю страховую сумму S по

Равенство (5.19) является приближённым, так как величина S

является случайной, а именно, зависит от воли страхователей и до заключения договоров неизвестна. В методике I равенство (5.19)

постулируется, что является её недостатком. В работе [9] этот недостаток устранён, нетто-ставка получена в предположении, что S –

случайная величина. Впрочем, если число договоров n достаточно

велико, то равенство (5.19) является достаточно точным.

Из (5.17), (5.18), и (5.19) получается уравнение для нетто-ставки Тн :

Решая (5.20), находим

83

Основа нетто-ставки в Методике I Росстрахнадзора, определяемая по формуле (5.22), совпадает с оценкой убыточности страховой суммы.

Действительно, убыточность у (со 100 рублей страховой суммы)

определяется равенством

Если вспомнить, что mn есть статистическая вероятность наступления страхового события, близкая к величине q, то формулы

(5.22) и (5.24) окажутся практически идентичными. Таким образом,

основы нетто-ставки в этих двух методиках принципиально совпадают.

Основа нетто-ставки соответствует средним выплатам страховщика,

зависящим от вероятности наступления страхового случая q, средней страховой суммы S и среднего возмещения S в . Рисковая надбавка учитывает вероятные повышения количества страховых случаев относительно их среднего значения.

84

Пример 5.1. Страховая компания заключает договоры

имущественного страхования с параметрами: вероятность наступления страхового случая равна 0,03, средняя страховая сумма по одному договору равна 800 руб., среднее возмещение при наступлении страхового случая равно 300 руб., количество договоров 500, среднее квадратическое отклонение от среднего возмещения равно 35 руб.,

Таким образом, брутто-ставка составляет 2 рубля 13 коп. со 100

рублей страховой суммы.

Во многих случаях, особенно при расчёте тарифных ставок по новым видам страхования, статистика страховых сумм и возмещений отсутствует. В такой ситуации приходится оценивать максимальные значения рисковой надбавки и основы нетто-ставки так, чтобы полученные оценки уже не содержали некоторые из неизвестных параметров. Эти оценки и принимаются за нетто-ставки при отсутствии статистики.

Оценим рисковую надбавку при неизвестном коэффициенте вариации Sв . На рисунках 5.3 – 5.6 приведены иллюстрации возможных плотностей распределений выплат со средними значениями

S в .

85

1. На рисунке 5.3 пик распределения выплат находится вблизи S в ,

выплаты тесно сгруппированы около средней, отношение Sв

относительно невелико.

2. На рисунке 5.4 пик распределения выплат также находится вблизи Sв ,

но кривая распределения является более пологой, чем на рисунке 5.4,

следовательно, разброс выплат вокруг средней больше и отношение

Sв больше, чем в предыдущем случае.

3. На рисунке 5.5 изображён предельный по отношению к первым двум вариантам случай, когда равновероятно появление выплат как вблизи

средней выплаты Sв , так и на границах их возможных значений. В

данном случае коэффициент вариации будет максимальным среди первых трех вариантов.

4. На рисунке 5.6 изображён самый опасный для страховщика, но практически не реализуемый в действительности случай, когда выплаты сосредоточены на границах их возможных значений – около 0 и Sв max.

При этом значение / Sв

86

Пример 5.3. Страховая компания заключает договор страхования автотранспортных средств от угона. Согласно статистике органов УВД региона, вероятность угона автотранспортных средств страхуемых марок равна 0,15. При количестве договоров 100% гарантии безопасности 0,95 и доле нагрузки 25% найти брутто-ставку.

Решение. Разброс возмещений неизвестен, следовательно,

необходимо воспользоваться формулой (5.30). Далее средняя страховая сумма и среднее возмещение также неизвестны. Поэтому согласно рекомендациям Росстрахнадзора, в формуле (5.30) коэффициент убыточности можно взять равным 0,4:

Как указывалось выше, методика Росстрахнадзора (I) обусловлена рядом формальных и скрытых предположений. К наиболее существенным скрытым предположениям относится допущение, что страховые суммы по всем договорам страхового портфеля совпадают. В

работе [9] было получено обобщение методики (I), где страховые суммы

Si по различным договорам рассматривались как случайные величины.

При этом для нетто-ставки Тн была получена следующая формула

89

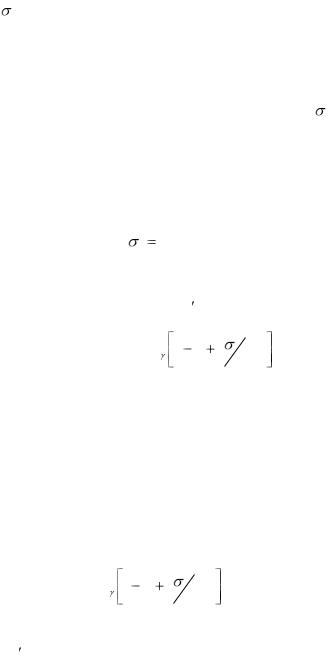
где 1 - среднее квадратическое отклонение страховой суммы по одному договору от средней страховой суммы. Формула (5.31) уже учитывает разброс страховых сумм по различным договорам относительно средней страховой суммы с помощью показателя 1 . Формула (5.31) обобщает формулу (5.21). При этом основа нетто-ставки в формуле (5.31)

совпадает с основой нетто-ставки, определяемой по формуле (5.22), а

рисковая надбавка из (5.31) не совпадает с формулой (5.23). Если же

Это означает, что при малых значениях n, удовлетворяющих неравенству (5.32) нетто-ставка из «Методики (I)», рассчитанная по формуле (5.21), оказывается заниженной и не обеспечивает заданной гарантии безопасности.

Если выполняется неравенство

то Т н < Тн , то есть нетто-ставка из «Методики (I)» оказывается завышенной. Следует отметить, что Федеральная служба страхового надзора не возражает против завышения тарифов, так как в этом случае финансовая устойчивость страховой организации повышается.

Существенные возражения при занижении тарифа могут возникнуть по двум обстоятельствам. Во-первых может понизиться финансовая устойчивость страховой организации. Во-вторых, у страховой организации могут обнаружиться признаки стратегии демпингования.

Пример 5.4. Страховая компания заключает договора имущественного страхования с параметрами: вероятность наступления

90

страхового случая равна 0,03, средняя страховая сумма по одному договору равна 800 рублей, среднее квадратическое отклонение от средней страховой суммы равно 150 рублей, среднее возмещение при наступлении страхового случая равно 300 рублей, количество договоров

500, среднее квадратическое отклонение от среднего возмещения равно

35 рублей, гарантия безопасности 0,9, доля нагрузки в брутто-ставке равна 30 %. Найти брутто-ставку.

Решение. Найдём основу нетто-ставки: Т0 = 100 × 0,03 × 800300 1,12.

Рисковая надбавка:

Таким образом, брутто-ставка составляет 2 рубля 16 копеек со 100

рублей страховой суммы. Следовательно, брутто-ставка, рассчитанная по уточнённой методике оказалось больше, чем рассчитанная по методики (1) Росстрахнадзора в примере 5.1. Следует отметить, что разница небольшая, всего лишь 3 копейки.

В завершение параграфа можно отметить, что имеются и другие обобщения Методики (I) Росстрахнадзора. Так в работе [7] дано обобщение Методики (I), учитывающее инфляцию и наращение страховых резервов.

5.3. Методика Росстрахнадзора (II)

Настоящая методика так же, как и методика (I), используется для получения нетто-ставок в массовых рисковых видах страхования. В

некотором смысле эта методика дополняет методику (I), так как в ней не предъявляется требование независимости наступления страховых

91