
Астахов Основные разделы механики 2011
.pdf
Потенциальная энергия упругодеформированной пружины
Пупр |
= |
кx |
2 |
+ C, |
(15.9) |
2 |
|
||||
|
|
|
|
|
где х — смещение незакрепленного конца пружины; к — жесткость пружины, С — произвольная постоянная (выбирается из условия удобства решения задачи).
Графики П(х) при различных постоянных: а) С > 0, б) С = 0, в) С < 0 параболы (рис. 15.1).
При условии П (0) = 0 постоянная С = 0 и
Пупр |
= |
кx |
2 |
. |
(15.10) |
2 |
|
||||
|
|
|
|
|
Пупр  )
)
б) в)
0 x
Рис. 15.1
Потенциальная энергия материальной точки в однородном поле сил тяжести
Птяж = mgh + C, |
(15.11) |
где m — масса; h — высота м.т. над поверхностью Земли; g = const; С — произвольная постоянная.
Графики Птяж(h) при различных постоянных: а) С > 0, б) С = 0, в) С < 0 прямые линии (рис. 15.2).
При условии: Птяж(0) = 0 постоянная С = 0 и
Птяж = mgh. |
(15.12) |
Птяж
a)
б)
0в) h
Рис. 15.2
Механическая энергия м.т. (системы м.т.) E — СФВ, равная сумме кинетической и потенциальной энергий м.т. (системы м.т.):
E = K + П. |
(15.13) |
Единица механической энергии — джоуль: [Е] = Дж.
51
Приращение механической энергии м.т. (системы м.т.) E
равно сумме приращений кинетической и потенциальной энергий м.т. (системы м.т.):
E = K + П. |
(15.14) |
Замкнутая консервативная система м.т. (з.к.с) — замкнутая система м.т., в которой действуют только консервативные силы.
Закон сохранения механической энергии
Механическая энергия замкнутой консервативной системы не изменяется с течением времени при движении м.т. системы:
Eз.к.с = const. |
(15.15) |
Уравнению (15.15) эквивалентно уравнение: |
|
E з.к.с = 0. |
(15.16) |
Замкнутая (неконсервативная) система м.т. (з.с) — замкну-
тая система м.т., в которой наряду с консервативными действуют внутренние неконсервативные силы.
Полная энергия системы м.т. W — СФВ, равная сумме внут-
ренней U (сумма кинетической и потенциальной энергий молекул тел) и механической E м.т.:
W = U +E. |
(15.17) |
Закон сохранения полной энергии
Полная энергия замкнутой (неконсервативной) системы м.т.
не изменяется с течением времени при движении материальных точек системы:
Wз.с = const. |
(15.18) |
Уравнению (15.18) эквивалентно уравнение: |
|
W з.с = 0. |
(15.19) |
Приращение внутренней энергии замкнутой (неконсерватив-
ной) системы м.т. равно убыли ее механической энергии:
Uз.с = – Eз.с. |
(15.20) |
52
Приращение механической энергии замкнутой (неконсерва-
тивной) системы м.т. равно работе внутренних неконсервативных сил:
E з.с = A внутр.нк.сл. |
(15.21) |
Незамкнутая (неконсервативная) система м.т. (нз.с) — не-
замкнутая система м.т., в которой наряду с консервативными силами действуют внутренние и внешние неконсервативные силы.
Механическая энергия незамкнутой (неконсервативной) сис-
темы м.т. равна сумме кинетической энергии системы Kc, потенциальной энергии системы Пc и потенциальной энергии ее м.т. во внешнем силовом поле Пвнеш:
Eнз.с = Kс + Пс + Пвнеш. |
(15.22) |
Приращение механической энергии незамкнутой (неконсерва-
тивной) системы м.т. равно работе внутренних и внешних неконсервативных сил:
Eнз.с = Aнк.сл = Aвнутр.нк.сл + Aвнеш.нк.сл. |
(15.23) |
Соударение однородных шаров
Абсолютно упругий удар шаров — удар, при котором силы взаимодействия между шарами являются консервативными.
Центральный удар однородных шаров — удар, при котором скорости шаров направлены вдоль линии, соединяющей центры шаров.
Скорости однородных шаров после центрального абсолютно упругого удара определяются с использованием законов сохранения импульса и механической энергии системы.
Абсолютно неупругий удар шаров — удар, при котором силы взаимодействия между шарами являются неконсервативными. Механическая энергия системы не сохраняется и частично или полностью переходит во внутреннюю энергию шаров.
Скорости двух однородных шаров после абсолютно неупругого центрального удара становятся одинаковыми и равными скоро-
сти центра масс шаров до удара (при Fp.внеш = 0, см. равенство 13.20). Для определения приращения внутренней энергии шаров
используется уравнение (15.20).
53
|
|
|
|
ПРИЛОЖЕНИЕ 1 |
||
|
Греческий алфавит |
|
|
|
||
|
|
|
|
|
|
|
Α α (альфа) |
Β β (бета) |
Γ γ (гамма) |
|
δ (дельта) |
|
|
Ε ε (эпсилон) |
Ζ ζ (дзета) |
Η η (эта) |
|
Θ θ (тэта) |
|
|
Ι ι (йота) |
Κ κ (каппа) |
Λ λ (ламбда) |
|
Μ μ (мю) |
|
|
Ν ν (ню) |
Ξ ξ (кси) |
Ο ο (омикрон) |
|
Π π (пи) |
|
|
Ρ ρ (ро) |
Σ σ (сигма) |
Τ τ (тау) |
|
Υ υ (ипсилон) |
|
|
Φ ϕ (фи) |
Χ χ (хи) |
Ψ ψ (пси) |
|
Ω ω (омега) |
|
|
|
Латинский алфавит |
|
|
|
||
|
|
|
|
|
|
|
Α a (а) |
Β b (бе) |
|
C c (це) |
|
D d (де) |
|
Ε e (е) |
F f (эф) |
|
G g (ге) |
|
H h (аш) |
|
I i (и) |
J j (йот) |
|
K k (ка) |
|
L l (эль) |
|
M m (эм) |
N n (эн) |
|
O o (о) |
|
P p (пэ) |
|
Q q (ку) |
R r (эр) |
|
S s (эс) |
|
T t (тэ) |
|
U u (у) |
V v (ве) |
|
W w (дубль-ве) |
|
X x (икс) |
|
Y y (игрек) |
Z z (зет) |
|
|
|
|
|
54
ПРИЛОЖЕНИЕ 2
Единицы физических величин
Международная система единиц имеет сокращенное название
SI (от начальных букв Systeme International d′Units) или в рус-
ской транскрипции СИ.
Она построена (1960 1983 г.) на семи основных и двух дополнительных единицах. В механике используются часть основных и дополнительных единиц, которые приведены в табл. П2.1
|
|
|
Таблица П2.1 |
|
|
|
|
|
|
Физическая вели- |
Единица |
Обозначение |
||
чина |
|
|
|
|
|
русское |
международное |
|
|
|
|
|
||
|
|
|
|
|
Длина |
метр |
м |
m |
|
Масса |
килограмм |
кг |
kg |
|
Время |
секунда |
с |
s |
|
Плоский угол |
радиан |
рад |
rad |
|
Метр равен длине пути, проходимого светом в вакууме за промежуток времени 1/299 792 458 с (1983 г).
При таком определении метра скорость света в вакууме равна точно 299 792 458 м/с.
Первоначально (1791 г.) метр определялся как одна десятимиллионная часть четверти земного меридиана, после измерения которого был изготовлен прототип метра.
Килограмм равен массе международного прототипа килограмма, который хранится в Международной палате мер и весов в г. Севре, Франция.
Секунда равна 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия-133, не возмущенного внешними полями.
Первоначально (1791 г.) секунда определялась как 1/86400 часть средних солнечных суток.
Радиан равен углу между двумя радиусами окружности, длина
55

дуги между которыми равна радиусу.
Производные единицы
Производная единица образуется согласно уравнению, связывающему данную физическую величину с другими физическими величинами, единицы которых известны.
Таким образом, производная единица физической величины представляет собой произведение основных и дополнительных единиц, возведенных в некоторые (соответствующие физическому уравнению) целочисленные степени, которые могут быть положительными, отрицательными или равными нулю.
Например, единица скорости согласно уравнению (1.12) — метр в секунду (м/с), единица ускорения согласно уравнению (3.2)
— метр на секунду в квадрате (м/с2).
Применяются также внесистемные единицы, некоторые из которых приведены в табл. П2.1.
|
|
Таблица П2.1 |
||
|
|
Содержит |
|
|
Величина |
Единица |
|
||
|
|
единиц СИ |
|
|
Время |
минута (мин) |
60 с |
|
|
|
час (ч) |
3,6 103 с |
|
|
|
сутки (сут) |
8,64 104 с |
|
|
Масса |
тонна (т) |
103 кг |
|
|
Объем |
литр (л) |
10─3 м3 |
|
|
Плоский угол |
градус ( ° ) |
1,75 10─2 рад |
|
|
Работа |
ватт-час (Вт ч) |
3,6 103 Дж |
|
|
Мощность |
лошадиная сила |
7,35 102 Вт |
|
|
Давление |
миллиметр ртутного столба |
1,33 102 Па, |
|
|
|
(мм рт. ст.), |
|
|
|
|
физическая атмосфера (атм) |
1,01 105 Па |
|
|
56
ПРИЛОЖЕНИЕ 3
Система координат
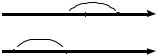
Прямолинейная координатная ось Ox (Oy,Oz) — прямая линия с выбранными положительным направлением (отмечается стрелкой), началом отсчета и единичным отрезком (масштабом).
Начало отсчёта — любая точка (обозначается буквой О), принадлежащая оси. Точка О делит ось на положительную (вдоль
положительного направления) и |
отрицательную |
полуоси |
||||||||||
(рис. П3.1). |
|
|
|
|
|
|
|
|
L |
|
|
|
|
Единичный (масштабный) от- |
а) |
|
|
|
|
|
|
|
|||
резок служит для измерения длин |
|
L О |
1 |
M |
x |
|||||||
отрезков оси (расстояний между |
б) M |
|
|
|
|
|
|
|
||||
точками на оси) в единицах некото- |
О |
|
|
x |
||||||||
|
|
|
||||||||||
1 |
|
|||||||||||
рой величины (например, длины). |
|
Рис. П3.1 |
|
|||||||||
|
Координата точки, принадле- |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
||||
жащей оси Ox (обозначается x) — величина, равная: |
|
|
|
|
||||||||
|
а) длине L отрезка между началом отсчета и данной точкой: |
|
||||||||||
|
|
|
|
x = L, |
|
|
|
|
|
|
(П3.1) |
|
если |
точка |
находится |
на |
положительной |
полуоси |
(т.М |
на |
|||||
рис. П3.1а); |
|
|
|
|
|
|
|
|
|
|
|
|
|
б) длине L отрезка между началом отсчета и данной точкой, |
|||||||||||
умноженной на минус единицу: |
|
|
|
|
|
|
|
|
||||
|
|
|
|
x = −L, |
|
|
|
|
|
|
(П3.2) |
|
если |
точка |
находится |
на |
отрицательной |
полуоси |
(т.М |
на |
|||||
рис.П3.1б). |
|
|
|
|
|
|
|
|
|
|
|
|
|
Прямоугольная (декартова) система координат на плоскости |
|||||||||||
— система, состоящая из двух взаимно перпендикулярных прямолинейных координатных осей. Точка пересечения осей называется началом координат и обозначается буквой О.
На рис. П3.2 представлена система прямоугольных координат xOy. Ось Ox называется также осью абсцисс, ось Oy — осью орди-
нат.
Проекция точки на ось — точка пересечения перпендикуляра, проведенного из данной точки к оси, с этой осью.
57
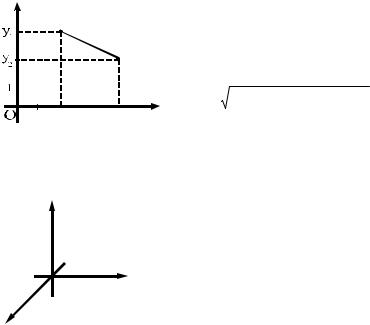
Координатой х (или y) точки, принадлежащей плоскости xOy
|
|
|
|
|
(рис. П3.2) |
является координата |
х |
||
y |
|
(или y) проекции данной точки на ось |
|||||||
|
Ox (или Oy). |
|
|
|
|||||
|
|
|
N1 |
|
|
|
|
||
|
|
|
d |
|
Расстояние d между двумя точ- |
||||
|
|
|
|
N2 |
ками |
N1(x1,y1) и N2(x2,y2), |
располо- |
||
|
|
|
|
женными на плоскости xOy: |
|
|
|||
|
|
|
|
|
|
|
|||
|
|
|
1 x1 |
x2 x |
d = |
(x1 − x 2 )2 + (y1 − y2 )2 |
, (П3.3) |
||
|
|
|
|||||||
|
|
|
где x1 и y1 — координаты точки N1, x2 |
||||||
|
|
Рис. П3.2 |
|
||||||
|
|
|
и y2 |
— |
координаты точки |
N2 |
|||
|
|
|
|
|
|||||
(рис. П3.2).
Прямоугольная (декартова) система координат в простран-
zстве — система, состоящая из трех взаимно перпендикулярных координатных осей, пересекающихся в одной точке, которая
|
является началом координат. |
|
О |
На рис. П3.3 представлена правая сис- |
|
тема координат в пространстве, в которой |
||
y |
||
|
кратчайший поворот положительной полу- |
xоси Ox к положительной полуоси Oy виден со стороны положительной полуоси Oz
Рис. П3.3 происходящим против хода часовой стрелки. Ось Oz называется также осью аппликат.
58
ПРИЛОЖЕНИЕ 4
Скаляры. Функции и графики.
Скаляр — величина, определяемая одним числом. Скаляр не зависит от направления в пространстве.
Две однородные скалярные физической величины равны, если при измерении их одной и той же единицей получаются одинаковые числа.
Приращение (изменение) некоторой величины A — разность между конечным (Aк) и начальным (Aн) значениями этой величины:
A = Aк − Aн . |
(П4.1) |
Убыль (разность) некоторой величины A — разность между начальным (Aн) и конечным (Aк) значениями этой величины:
′ |
(П4.2) |
А = Ан − Ак . |
Между убылью и приращением величины A выполняется соотношение:
′ |
А. |
(П4.3) |
А = − |
||
Убыль ´A часто обозначают − |
A. |
|
Функция y = f(x) или y = y(x) — правило, по которому каждому числу x сопоставляется число y.
Числа x называются значением аргумента функции, числа y — значением функции (в точке x).
Область определения функции D — множество X чисел x. Область значений функции R — множество Y чисел y.
График функции y(x) — множество точек на координатной плоскости xOy (Приложение 1) с координатами (x,y).
Графиком функции может быть некоторая линия. Линейная функция функция первой степени от аргумента:
y = ax + b, |
(П2.4) |
где а (а ≠ 0) и b некоторые константы.
Графиком линейной функции является прямая линия, тангенс
59
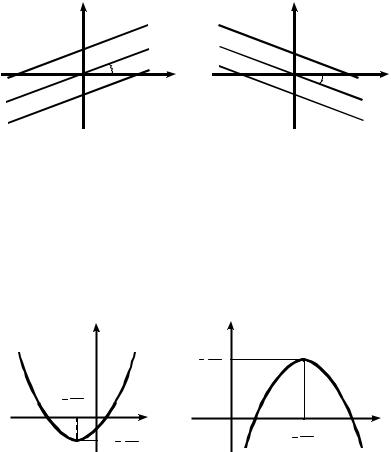
угла наклона которой к оси Оx равен постоянной при аргументе функции:
tgα = a. |
(П4.5) |
На рис. П2.1 приведены графики этой функции при различных постоянных а и b.
y |
|
0 |
|
y |
|
|
a |
< |
b <0 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
a< 0 |
|
|
|
α |
b=0 |
|
x |
||
О |
b< 0 |
|
α |
|||
|
|
|
x |
О |
b <0 |
|
|
|
|
|
|
|
b=0 |
а) |
|
|
|
б) |
|
b<0 |
|
|
Рис. П2.1 |
|
|
||
|
|
|
|
|
|
|
Квадратичная функция функция второй степени от аргумента:
y = ax2 + bx + c , |
(П2.4) |
где а (а ≠ 0), b и с некоторые константы.
Графиком квадратичной функции является парабола. График этой функции при а > 0 приведен на рис. П2.2а, при а < 0 на рис. П2.2б.
y |
|
a <0 |
|
b |
x |
2a |
|
О |
b2 |
c |
4a |
а) |
|
|
y |
a<0 |
|
c |
b2 |
|
|
|
|
||
4a |
|
|
|
|
О |
b |
x |
|
|
2a |
|
Рис. П2.2 |
б) |
|
|
|
|
||
60
