
Астахов Основные разделы механики 2011
.pdfдинат Ох и Оу, показанных на рис. 6.1, и их подстановки в уравнения (6.3) – (6.6) получаются равенства (при хн = 0, ун = 0, tн = 0)
для проекций скорости:
|
vx = v0cosα0, |
|
|
|
|
(6.7) |
|||||||
vy = v0sinα0 – gt; |
|
|
(6.8) |
||||||||||
для координат: |
|
x = v0cosα0 t, |
|
|
|
|
(6.9) |
||||||
|
|
|
|
|
|
||||||||
y = v0sinα0 t − |
gt2 |
. |
|
(6.10) |
|||||||||
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Решая совместно равенства (6.7) ÷ (6.10), можно определить: |
|||||||||||||
время подъёма на максимальную высоту |
|
|
|
|
|
|
|||||||
tпод = |
v0sinα0 |
|
, |
|
|
|
(6.11) |
||||||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
g |
|
|
|
|
|
|
|
|
время движения (при ук = ун) |
|
|
|
|
|
|
|
|
|
|
|
|
|
tдв = |
|
2v0 sin α0 |
= 2tпод, |
(6.12) |
|||||||||
|
|
|
|||||||||||
|
|
g |
|
|
|
|
|
|
|
|
|
||
максимальную высоту подъёма |
|
|
|
|
|
|
|
|
|
||||
ymax |
= H = |
v2 sin2 |
α |
0 |
, |
(6.13) |
|||||||
0 |
|
|
|
|
|
||||||||
|
2g |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
максимальную дальность полёта |
|
|
|
|
|
|
|
|
|
||||
xmax |
= L = |
|
v2 sin 2α |
0 |
, |
(6.14) |
|||||||
|
0 |
|
|
|
|
|
|||||||
|
|
g |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
уравнение траектории (при движении м.т. в плоскости хОу)
y (x)= tgα0 x − |
g |
|
x2 |
(6.15) |
2v02cos2 |
|
|||
|
α0 |
|
||
(траекторией м.т. является парабола, представленная на рис. 6.1),
21

зависимость проекции скорости на ось Oy от высоты h: при подъёме
vy = |
v02 sin2 α0 − 2gh, |
(6.16) |
при спуске |
|
|
vy = − |
v02 sin2 α0 − 2gh, |
(6.17) |
модуля скорости от высоты |
|
|
v = v02 − 2gh. |
(6.18) |
|
При выборе другой системы координат, отличающейся от системы, показанной на рис. 6.1, уравнения (6.3) — (6.6) не изменяются, некоторые (или все) уравнения (6.7) — (6.10) изменятся. Так, например, если ось Оу будет направлена вертикально вниз (направление оси Ох не изменяется), то
vy = −v0sinα0 + gt, |
|
(6.19) |
||
y = −v0sinα0 t + |
gt2 |
. |
(6.20) |
|
2 |
||||
|
|
|
||
§7. Движение по окружности
Равномерное движение материальной точки по окружности
— движение, при котором м.т. за любые равные промежутки времени проходит одинаковые по длине дуги окружности.
|
y |
|
|
|
|
|
Является частным случаем равномер- |
|
vк |
|
rк |
vн |
|
|
ного движения материальной точки. |
||
|
|
|
||||||
|
|
|
|
|||||
|
|
|
|
|
|
|
Скорость (линейная скорость) м.т., |
|
|
|
|
Δϕ |
r |
|
|
движущейся |
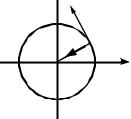
по окружности радиуса R |
|
|
|
|
н |
|
|
(рис. 7.1), перпендикулярна радиус-вектору |
|
|
O |
|
|
R |
x |
|||
|
|
|
м.т. (начало координат совпадает с центром |
|||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
окружности). |
|
|
|
|
|
|
|
|
Модуль |
скорости при равномерном |
|
Рис. 7.1 |
|
|
|
||||
|
|
|
|
движении материальной точки по окруж- |
||||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
22 |
|
ности не изменяется:
v = const. |
(7.1) |
Модуль угловой скорости (в дальнейшем — угловая скорость)
ω — СФВ, равная пределу отношения угла поворота Δϕ радиусвектора м.т. к промежутку времени t, за который произошёл этот поворот, при бесконечном уменьшении промежутка времени:
ω= lim |
ϕ |
. |
(7.2) |
|
|||
t→0 |
t |
|
|
Единица угловой скорости — радиан в секунду: [ ω ] = рад/с.
Соотношение между модулем линейной скорости и угловой скоростью:
v = ωR, |
(7.3) |
где R — радиус окружности, являющейся траекторией материальной точки.
При равномерном движении материальной точки по окружности за любые равные промежутки времени углы поворота радиусвектора м.т. одинаковы.
Угловая скорость при равномерном движении м.т. по окруж-
ности — величина, равная отношению угла поворота Δϕ радиусвектора м.т. к промежутку времени t, за который произошёл этот поворот:
ω= |
Δϕ |
= const. |
(7.4) |
|
t |
|
|
Ускорение при таком движении является нормальным (aτ = 0), которое называется также центростремительным:
an = aцc; |
(7.5) |
оно направлено к центру окружности (рис. 7.2) и противоположно радиус-вектору материальной точки:
aцс = −ω2r. |
(7.6) |
23
Модуль центростремительного ускорения прямо пропорцио-
нален квадрату угловой скорости:
y v
v
aцс 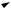 r
r
O |
R x |
Рис. 7.2
aцс = ω2R, |
(7.7) |
и квадрату модуля линейной скорости:
aцс = |
v2 |
. |
(7.8) |
|
R |
||||
|
|
|
Период обращения T — промежуток времени, в течение которого м.т. совершает один оборот (радиус-вектор м.т. поворачивается на угол, равный 2π радиан):
T = |
t |
, |
(7.9) |
|
N |
|
|
где N — число оборотов м.т. за промежуток времени |
t. |
||||||
Путь м.т. за один период равен длине окружности. Модуль ли- |
|||||||
нейной скорости может быть найден по формуле: |
|
||||||
v = |
2πR |
. |
(7.10) |
||||
|
|
|
|
|
|||
|
|
T |
|
||||
Частота обращения n — СФВ, равная отношению числа обо- |
|||||||
ротов N, совершенных м.т. за промежуток времени |
t, к этому |
||||||
промежутку времени: |
|
||||||
n = |
|
N |
. |
(7.11) |
|||
|
|
|
|||||
|
|
|
t |
|
|||
Единица частоты обращения — обратная секунда:[ n ] = с−1. |
|||||||
Соотношения между |
|
||||||
угловой скоростью ω и частотой n: |
|
||||||
ω = 2πn, |
(7.12) |
||||||
периодом Т и частотой n: |
|
||||||
Т = |
1 |
, |
(7.13) |
||||
|
|||||||
|
|
|
n |
|
|||
24 |
|
|
|
|
|
|
|
периодом Т и угловой скоростью ω:
T = |
2π |
. |
(7.14) |
|
|||
|
ω |
|
|
§8. Движение твёрдого тела
Произвольное движение твёрдого тела можно разложить на два вида движения: поступательное и вращательное.
Поступательное движение твердого тела — движение, при котором любая прямая, соединяющая произвольные точки тела, остаётся параллельной своему начальному положению в пространстве. Все точки тела при поступательном движении имеют конгруэнтные (совпадающие при наложении) траектории.
Вращательное движение (вращение) твердого тела — движе-
ние, при котором все точки тела движутся по окружностям, центры которых лежат на одной прямой — оси вращения, перпендикулярной плоскостям окружностей.
Угловая скорость вращения твердого тела — угловая ско-
рость любой точки твердого тела (радиус-вектор этой точки лежит в плоскости, перпендикулярной оси вращения, при этом начало его находится в точке, принадлежащей оси вращения).
Плоское движение твердого тела — движение твердого тела,
при котором все точки этого тела движутся в плоскостях, параллельных некоторой плоскости.
При плоском движении скорость любой точки твердого тела может быть представлена в виде суммы скорости поступательного движения vпос некоторой прямой, являющейся осью вращения, и скорости (линейной скорости) вращательного движения данной
точки vвр вокруг этой оси: |
|
vт = vпос+ vвр, |
(8.1) |
Величина угловой скорости вращения одинакова для всех точек твердого тела и не зависит от выбора оси вращения (которая может находиться вне тела).
Примером плоского движения является качение круглого
25

прямого цилиндра по плоской горизонтальной поверхности опоры. Если точки цилиндра, принадлежащие его оси, имеют постоянную скорость vсп относительно поверхности опоры (системы отсчёта, связанной с этой поверхностью), то угловая скорость вращения цилиндра (угловая скорость точек цилиндра, не принадлежа-
щих оси вращения)
ω= |
vсп |
, |
(8.2) |
|
|||
|
R |
|
|
где R — радиус цилиндра.
Скорость любой точки цилиндра относительно поверхности опоры vтп может быть найдена из равенства, подобного соотноше-
нию (2.21):
vтп = vсп + vтс, |
(8.3) |
где vтс — скорость точки относительно оси цилиндра (системы отсчета, связанной с этой осью), которая обусловлена вращением цилиндра вокруг своей оси.
Например, скорость т.В относительно поверхности опоры (на рис. 8.1 и рис. 8.2 показано основание цилиндра)
vвп = vсп + vвс = 2vсп, |
(8.4) |
поскольку модуль скорости т. В относительно оси |
цилиндра |
vвс = ωR = vсп.
Скорость любой точки цилиндра относительно поверхности
|
опоры |
можно также определить |
|||||
|
как линейную скорость при только |
||||||
|
одном |
вращательном |
движении |
||||
|
цилиндра с угловой скоростью ω |
||||||
|
вокруг |
мгновенной |
оси |
вращения |
|||
|
— оси, скорость точек которой от- |
||||||
|
носительно этой поверхности рав- |
||||||
|
на нулю. |
|
|
|
|
||
|
При |
качении |
цилиндра |
без |
|||
Рис. 8.1 |
проскальзывания мгновенная |
ось |
|||||
вращения |
проходит через точки |
||||||
|
|||||||
касания цилиндра с поверхностью опоры (на рис. 8.1 и рис. 8.2 показана точка А, принадлежащая этой оси).
26
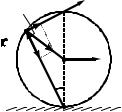
Скорость любой точки цилиндра при таком вращении перпендикулярна радиус-вектору, начало которого находятся на мгновенной оси вращения, а конец в выбранной точке. Этот радиусвектор лежит в плоскости, перпендикулярной мгновенной оси вращения. Например, скорость т. P относительно поверхности опоры (рис. 8.2) перпендикулярна радиус-вектору rАР, начало и конец которого находятся в т. А и в т. P соответственно, и направлена по линии, проходящей через т. B, лежащую на вертикальном диаметре с точкой А.
Модуль скорости выбранной точки определяется равенством:
vрп = ωrАР, |
(8.5) |
|
|
B vP |
|
где rАР — модуль радиус-вектора выбранной |
apτ |
||||
точки Р. |
|
P |
ap |
|
|
Так, абсолютная величина скорости т.В, |
|
|
vC |
||
AP |
|||||
модуль радиус-вектора которой rАВ = 2R (см. |
apn |
C |
|||
рис. 8.1), согласно формулы (8.5) |
|
|
|
|
|
vВП = rАВω = 2Rω = 2vсп, |
(8.6) |
|
|
α |
|
|
|
|
|
||
что совпадает со значением, найденным по |
|
|
A |
|
|
формуле (8.4). |
|
|
|
Рис. 8.2 |
|
Ускорение любой точки цилиндра атп
относительно поверхности опоры может быть найдено из равенства, подобного соотношению (3.13):
атп = атс + асп, |
(8.7) |
где атс — ускорение точки относительно оси цилиндра, обусловленное вращением цилиндра вокруг своей оси, асп — ускорение оси цилиндра относительно поверхности опоры.
При равномерном качении цилиндра асп = 0 и ускорение любой точки цилиндра как относительно оси цилиндра, так и относительно поверхности опоры, одно и то же, направлено к оси цилиндра и может быть определено из равенства:
a |
т |
= −ω2r , |
(8.8) |
|
т |
|
где rт — вектор, начало и конец которого находятся на оси цилиндра и в выбранной точке соответственно, лежащий в плоскости,
27
перпендикулярной оси вращения.
На рис. 8.2. показано ускорение ар точки Р, которое направлено к т. С, лежащей на оси цилиндра.
Модуль ускорения
a |
Р |
= ω2r = ω2R, |
(8.9) |
|
Р |
|
поскольку rР = R.
Относительно оси цилиндра ускорение ар является центростремительным (нормальным) ускорением. Относительно поверхности опоры ускорение точки Р может быть разложено на нормальное аpn и тангенциальное apτ ускорения (см. рис. 8.2), модули которых зависят от угла α между вертикалью и прямой АР:
аpn = арcosα, |
(8.10) |
|apτ| = арsinα. |
(8.11) |
28
ТЕМА 2. ДИНАМИКА
Динамика — раздел механики, в котором рассматривается взаимодействие тел и его влияние на их движение.
§9. Законы Ньютона
Классическая динамика основана на трёх законах Ньютона, являющихся обобщением большого количества опытных (экспериментальных) данных.
Механическое воздействие тел друг на друга — воздействие,
вызывающее деформацию (изменение размеров и формы тела) и ускорение (по отдельности или совместно) взаимодействующих тел.
Механическое взаимодействие происходит как между телами, находящимися в контакте, так и между телами, находящимися на некотором расстоянии друг от друга. В последнем случае взаимодействие осуществляется посредством силового поля — особого вида материи.
Сила F — ВФВ, являющаяся мерой механического воздействия на данное тело другого тела. Сила характеризуется направлением, абсолютной величиной и точкой приложения.
Единица силы — ньютон: [F] = Н = кг м/с2.
Система тел — тела, объединенные в группу при решении данной задачи.
Внутренние тела — тела, принадлежащие данной системе. Внешние тела — тела, не принадлежащие данной системе. Замкнутая система тел — система, ни одно из тел которой не
взаимодействует с внешними телами.
Незамкнутая система тел — система тел, хотя бы одно из которых взаимодействует с внешними телами.
Внутренние силы — силы, с которыми взаимодействуют тела, принадлежащие данной системе.
Внешние силы — силы, с которыми на тела данной системы действуют внешние тела.
Инертность — свойство тела, состоящее в том, что для изменения скорости тела при воздействии на него другого тела (или не-
29
скольких тел) требуется некоторый промежуток времени.
Гравитационное взаимодействие тел — взаимное притяжение тел, силы которого пропорциональны массам этих тел.
Масса тела m — СФВ, являющаяся мерой инертности тела и гравитационного взаимодействия тел.
Свойства массы: является положительной величиной (m > 0); не зависит от скорости тела (m = const); масса системы тел равна
n
сумме масс всех тел, входящих в эту систему ( mс = ∑mi , где n
i=1
— число тел системы); масса замкнутой системы тел остаётся неизменной при всех процессах, происходящих в этой системе
(mз.с = const).
Единица массы — килограмм: [m] = кг.
Первый закон Ньютона
Существуют системы отсчёта, называемые инерциальными системами отсчёта (ИСО), относительно которых материальная точка (м.т.) движется равномерно и прямолинейно или покоится, если на нее не действуют другие материальные точки.
Для решения некоторых задач систему, связанную с поверхностью Земли, можно считать инерциальной. Система отсчета, связанная с центром Солнца (гелиоцентрическая система) является инерциальной системой отсчета для решения задач с большей точностью.
Система отсчета, движущаяся относительно любой инерциальной системы отсчета с постоянной скоростью, также является инерциальной системой отсчета.
Свободная материальная точка — материальная точка, на которую не действуют другие материальные точки.
Первый закон Ньютона с использованием понятия “свободная материальная точка”: существуют системы отсчёта, называемые инерциальными системами отсчета (ИСО), относительно которых скорость свободной материальной точки
vсв.м.т = const |
(9.1) |
(в случае покоя свободной м.т. const = 0).
30
